با این مثال روشن میشود که: چرا شکل تنها یک مدل آزمایشی است و برای این که از نتیجه محاسبه و استدلال خود مطمئن شویم، باید از خود بپرسیم: آیا در واقع چنین شکلی وجود دارد؟
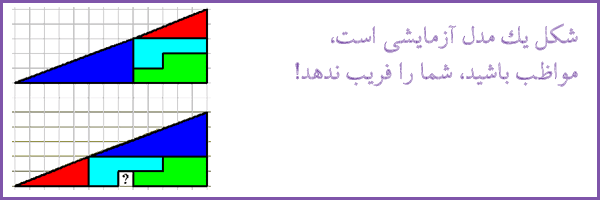
هر کسی که فعالیت میکند، اعم از اینکه فعالیتی علمی داشته باشد یا اجتماعی، همیشه با مسالههایی روبه رو میشود که، برای ادامه کار خود، ناچار است آنها را حل کند. همهی ما باید این توانایی را داشته باشیم که از موقعیتها و پیش آمدهای تازه نهراسیم و بتوانیم راه خروج ار بن بستها را بیابیم. برای این منظور، باید قبل از هر چیز، موقعیت مسالهی خود را مورد بررسی انتقادی قرار دهیم و با تجزیه و تحلیل دقیق آنها، دادهها و خواستها ی مساله را به خوبی بشناسیم، یعنی برای خود روشن کنیم که به چه هدف یا هدفهایی میخواهیم برسیم و برای رسیدن به آنها چه امکانهایی در اختیار داریم!
 |
عادت کردهایم برای حل مسالهی هندسی، از شکل استفاده کنیم. شکلی تقریبی و نه کاملا دقیق رسم میکنیم و روی آن، به جست و جوی هدف خود می رویم. و این، کار نادرستی نیست، هر وقت بتوانیم، برای مشکل خود و برای حل مسالهی خود، مدلی بسازیم، آزمایش روی آن، کار ما را سادهتر و ملموستر میکند و در نتیجه رابطهی بین هدف و امکانهای موجود را بهتر و شفافتر درک میکنیم. ذهن آدمی، بدون مدلسازی حتی نمیتواند کار استدلال را آغاز کند و در هندسه، بهترین مدل و بهترین دستگرهی مادی برای استدلال ذهنی، شکل است.
ولی توجه کنید که، کار روی مدل، نوعی آزمایش است و آزمایش نمیتواند جانشین استدلال ریاضی شود. ممکن است آزمایش روی یک مدل موفقیتآمیز باشد، ولی روی مدل دیگر، ما را به بن بست بکشاند. یکی از علتهای این وضع آن است که مدل، تنها بخشی از حقیقت موضوع مورد نظر ما را منعکس میکند نه تمامی آن را، مدل کاریکاتوری از حقیقت است و ممکن است بسیاری از جنبههای حقیقت را پنهان کرده باشد.
مدل مساله های هندسی، یعنی شکل هم، از این خصلت دور نیست. اینجا یعنی در شکلهای هندسی، عدم دقت در رسم و عدم توجه به ماهیت وجودی شکل ممکن است آن را از حقیقت دور کند. به این ترتیب، وقتی برای حل مساله هندسی، میخواهیم شکلی را رسم کنیم، علاوه بر توانایی در تجسم شکل و به خصوص شکلهای فضایی، باید همواره خود را برابر دو پوشش قرار دهیم:
|
آیا چنین شکلی میتواند وجود داشته باشد؟
آیا شکلی که رسم کردهایم، دست کم تا حد معقول، دقیق است؟
|
این دو پرسش، چندان مستقل از هم نیستند و شاید در تحلیل آخر، بتوان آنها را یکی دانست. تلاش میکنید، شکلی را با توجه به دادههای مساله تا حد امکان دقیق، رسم کنید، ولی موفق نمی شوید. به طور طبیعی از خودتان می پرسید: شاید اصلا چنین شکلی، با این شرطها وجود نداشته باشد؟ به طور کلی، عدم وجود شکل رسم آن را منتفی میکند و برعکس، رسم دقیق شکل وجود یا عدم وجود آن را روشن میسازد.
باوجود این، منطقیتر این است که، دو پرسش را از هم جدا کنیم و به هر کدام از آنها، به طور جداگانه پاسخ دهیم. پاسخ پرسش اول با تجزیه و تحلیل منطقی دادهها و پاسخ پرسش دوم با دقت در استفاده از ابزار رسم به دست میآید.
عدم توجه به این پرسشها و تنها آزمایش روی مدل ناقص خود، ممکن است ما را به نتیجهای به کلی دور از واقع برساند. با مثال زیر، مطلب روشنتر میشود.
مثال:
مساحت ذوزنقهای را پیدا کنید که بر دایرهای به شعاع برابر با R محیط شده است، به شرطی که بدانیم، یکی از زاویههای مجاور به قاعده برابر 60 درجه است، در ضمن، قطری از ذوزنقه که از راس این زاویه میگذرد، زاویه را نصف میکند و بر یکی از ساقهای ذوزنقه عمود است.
حل:
مدل خود را میسازیم. شکل 1. معرف مدل ماست،
در آن فرض کردهایم:
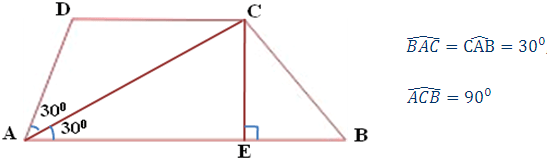
شکل 1
در ضمن|CE|=2R است.
زیرا در هر ذوزنقهای که بر دایرهای محیط باشد، طول ارتفاع برابر است با قطر این دایره.
در مثلث قائمالزاویهی ABC ، ضلع BC روبهرو به زاویهی 30 درجه است یعنی: |BC|=|AB|/2 . بنابراین در همین مثلث میتوان نوشت:
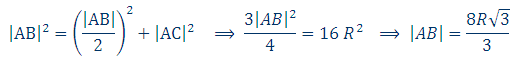
( |AC|=4R ، زیرا در مثلث قائمالزاویهی AEC= 2R |CE| روبهرو به زاویه ی 30 درجه است و بنابراین برابر 1/2 |AC| است).
مثلث ACD متساویالساقین است، زیرا:
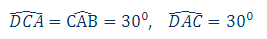
پس |AB|=|BC|. اگر ارتفاع DF از ذوزنقه را در نظر بگیریم، در مثلث AFD داریم:
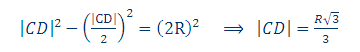
با در دست داشتن طولهای دو قاعده و طول ارتفاع ذوزنقه، مساحت آن بهدست میآید:
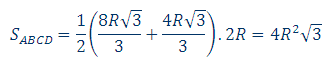
به ظاهر حل مسئله تمام شد، مساحت ذوزنقه به دست آمد. مسالهی ساده ای بود. در ضمن وقتی مساله را حل میکردیم از همهی دادهها استفاده کردیم: محیطی بودن ذوزنقه (آنجا که ارتفاع ذوزنقه برابر 2R گرفتیم). A = 600 و [AC]⊥[BC]، در ضمن قطر AC را نیمساز زاویهی A به حساب آوردیم. مشکل خاصی وجود دارد، مساله حل شد.
ولی اگر اندکی دقت کنیم، معلوم میشود، مساحت شکلی را پیدا کردهایم که در واقع وجود ندارد. چون چهار ضلعی محیطی است، باید داشته باشیم:
|AD|+|BC|=|AB|+|CD|
و چون |AD|=|CD|، پس |BC|=|AB|، یعنی باید در مثلث قائمالزاویه ی ABC، طول وتر با طول یکی از ضلعهای مجاور به زاویهی قائمه برابر باشد که ممکن نیست
.
با این مثال روشن میشود که: چرا شکل تنها یک مدل آزمایشی است و برای این که از نتیجه محاسبه و استدلال خود مطمئن شویم، باید از خود بپرسیم:
| آیا در واقع چنین شکلی وجود دارد؟ |
و ما دیدیم که در این مثال، با ذوزنقه ای سروکار داشتیم که، در واقع امر، وجود خارجی ندارد.
مثالهای زیادی از این قبیل، وجود دارد که آنها به عهدهی خوانندهی علاقه مند میگذاریم.
غلامرضا پورقلی
دانشجوی دکتری ریاضی
دانشگاه تهران