ضريب ثابت رابطهي 1 ميتواند بهگونهاي فاكتور گرفته شود كه بهصورت رابطهي ذيل درايد:
(رابطهي 4) با فاكتورگيري ميتوان ريشههاي رابطهي 2 را بهعنوان تابعي از 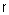 بهدست آورد. از آنچه تاكنون داشتهايم ميتوانيم ببيينم كه ضرايب رابطهي 2 ممكن است شبيه ذيل باشد: بهدست آورد. از آنچه تاكنون داشتهايم ميتوانيم ببيينم كه ضرايب رابطهي 2 ممكن است شبيه ذيل باشد:
رابطهي داده شده در اين مرحله داراي توانهاي .gif) ، ، .gif) و و .gif) است. اجازه ميدهيم ضرايب مذكور بهشكل ذيل بهدست آيند: است. اجازه ميدهيم ضرايب مذكور بهشكل ذيل بهدست آيند:
با بسط آن رابطهي ذيل بهدست خواهد آمد:
(رابطهي 5)
با مقايسهي رابطهي 3 با معادلهي داده شده (رابطهي 1)، متوجه ميشويم هيچ عبارت .gif) وجود نخواهد داشت؛ بنابراين رابطههاي ذيل را خواهيم داشت: وجود نخواهد داشت؛ بنابراين رابطههاي ذيل را خواهيم داشت: | - .gif) | | - از عبارت .gif) خواهيم داشت: خواهيم داشت:
(رابطهي 6) |
با استفاده از اين روابط ميتوانيم تركيب فصلي روابط ذيل را مشاهده كنيم: | - .gif)
(رابطهي 7) | | - .gif)
(رابطهي 8) |
اما سپس با آزمايش عبارت .gif) مشاهده خواهيم كرد كه مشاهده خواهيم كرد كه .gif) بايد بايد .gif) باشد بنابراين رابطهي ذيل برقرار خواهد بود: باشد بنابراين رابطهي ذيل برقرار خواهد بود:
(رابطهي 9) با فاكتورگيري از رابطهي 3 رابطهي ذيل بهدست خواهد آمد:
(رابطهي 10) اكنون ميتوانيم از فرمول درجهي چهار براي هر يك از ضرايب درجهي 4 استفاده كنيم كه در اين صورت چهار ريشه بهدست خواهد آمد: | .gif) | | و
| | .gif) |
با رسم نقاط .gif) يك ذوزنقه با با دو قاعده بهطول يك ذوزنقه با با دو قاعده بهطول .gif) و و .gif) و و .gif) ارتفاع بهدست خواهد آمد. از آنجايي كه مساحت «ذوزنقه» از رابطهي ذيل بهدست ميآيد خواهيم داشت: ارتفاع بهدست خواهد آمد. از آنجايي كه مساحت «ذوزنقه» از رابطهي ذيل بهدست ميآيد خواهيم داشت:
(رابطهي 11)
رابطهي 9 نشاندهندهي آن است كه مساحت «ذوزنقه» به متغير 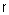 بستگي نداشته و برابر با 8 است. بستگي نداشته و برابر با 8 است.
بيان داده شده ميتواند بهصورت دو مربع نوشته و فاكتور گرفته شود:
(رابطهي 12)
بنابراين ريشههاي معادلهي اصلي (رابطهي 1) تركيبي از ريشههاي .gif) و و .gif) است. هر كدام از است. هر كدام از .gif) و و .gif) رابطهاي از درجهي 2 با ضرايب حقيقي هستند. رابطه از درجهي 2 مربوط به رابطهاي از درجهي 2 با ضرايب حقيقي هستند. رابطه از درجهي 2 مربوط به .gif) و و .gif) بهترتيب منجر به بهترتيب منجر به .gif) و و .gif) ميشوند. از آنجايي كه متغير ميشوند. از آنجايي كه متغير 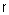 عددي حقيقي و غيرصفر است هر دو عبارت عددي حقيقي و غيرصفر است هر دو عبارت .gif) و و .gif) «منفي» خواهند بود بنابراين ريشههاي «منفي» خواهند بود بنابراين ريشههاي .gif) و و .gif) اصطلاحاً تشكيل «زوجهاي قرينه» ميدهند. اصطلاحاً تشكيل «زوجهاي قرينه» ميدهند. با استفاده از فرمول درجهي 2 ميتوانيم ريشههاي .gif) و و .gif) را بهترتيب براي را بهترتيب براي .gif) و و .gif) بهدست آوريم. اين دو ريشه و قرينههاي آنها يك «ذوزنقهي متساويالساقين» با محور حقيقي بهعنوان محور تقارن ميدهند. بهدست آوريم. اين دو ريشه و قرينههاي آنها يك «ذوزنقهي متساويالساقين» با محور حقيقي بهعنوان محور تقارن ميدهند. مساحت چنين ذوزنقهاي (جواب مورد انتظار مسأله) برابر است با حاصلضرب جمع نصف قاعدهها در ارتفاع آن:
(رابطهي 13)
در رابطهي 11، .gif) و و .gif) بهترتيب مشخصكنندهي بخشهاي «حقيقي» و «موهومي» عدد مختلط بهترتيب مشخصكنندهي بخشهاي «حقيقي» و «موهومي» عدد مختلط .gif) محسوب ميشوند. محسوب ميشوند.
از رابطهي 1 ميتوانيم روابط ذيل را بهدست آوريم:
(رابطهي 14)
بنابراين رابطهي ذيل برقرار است:
(رابطهي 15)
با استفاده از ريشهي درجهي دوم دو رابطهي ذيل بهدست خواهد آمد:
(رابطهي 16)
و
(رابطهي 17)
با اعمال فرمول درجهي دوم براي رابطهي 14، ريشههاي ذيل بهدست خواهد آمد:
و
با اعمال فرمول درجهي دوم براي رابطهي 15، ريشههاي ذيل بهدست خواهد آمد:
و
اين چهار «عدد مختلط» تشكيل يك «ذوزنقه» با ارتفاع .gif) و قاعدهها بهطول و قاعدهها بهطول .gif) و و .gif) ميدهد. بنابراين ميتوان مساحت آن را از رابطهي ذيل بهدست آورد: ميدهد. بنابراين ميتوان مساحت آن را از رابطهي ذيل بهدست آورد:
(رابطهي 18). |