آيا تاكنون از قضيهي آخر فرما براي اثبات يك حكم رياضي استفاده كردهايد؟



احتمالاً با قضیهی آخر فرما آشنایی دارید. پیر فرما، ریاضیدان بزرگ فرانسوی، در حدود 350 سال پیش مسألهای را در نظریهي اعداد مطرح كرد كه تا 11 سال پیش كسی موفق به حل آن نشد. در طول این سالها ریاضیدانان بزرگی وقت زیادی را صرف حل این مسأله نمودند ولی هیچیك نتوانستند مسأله را حل كنند.
البته بسیاری از ریاضیدانان مانند: گاوس، اویلر، لژاندر، سوفی ژرمن، هاردی، فالتینگنز، موردل و ... و خیلیهای دیگر، هریك پیشرفتی در حل مسأله بهوجود آوردند و در نهایت در سال 1994 اندرو وایلز آمریكایی با یك راه حل طولانی و با استفاده از مدرنترین تكنیكهای جبری، توپولوژی و هندسهی جبری موفق به كامل كردن این پیشرفتها شد و اثبات این قضیه بهنام وی ثبت گردید. صورت این قضیه این چنین است:
اگر n عددی طبیعی و بزرگتر از 2 باشد ( 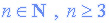 ) آنگاه معادلهی
) آنگاه معادلهی 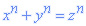 دارای هیچ جوابی در اعداد صحیح نیست.
دارای هیچ جوابی در اعداد صحیح نیست.
و اما سؤال مسابقه:
با استفاده از قضیه آخر فرما ثابت كنید اگر n >2 آنگاه 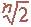 عددی گنگ است.
عددی گنگ است.
پاسخ
از برهان خلف کمک می گیریم:
پس فرض میکنیم 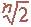 عددی گویاست، لذا a و b صحیح موجودند به قسمی که
عددی گویاست، لذا a و b صحیح موجودند به قسمی که 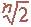 =a/b
=a/b
خواهیم داشت 2=an/bn
یعنی an=2bn
در نتیجه an=bn+bn
که با قضیهی آخر فرما در تناقض میباشد!