مجموعهها و زيرمجموعهها ... سؤال همراه با جواب
 سؤال
سؤال
فرض كنيد S يك زيرمجموعهي 70 عضوي از  باشد. ثابت كنيد
باشد. ثابت كنيد 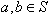 وجود دارند بهگونهاي كه:
وجود دارند بهگونهاي كه:


ابتدا لم ذيل را ثابت ميكنيم:
لم
چنانچه A يك زيرمجموعهي پنج عضوي 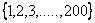 باشد. در اين صورت دو عضو
باشد. در اين صورت دو عضو 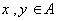 وجود دارند بهگونهاي كه:
وجود دارند بهگونهاي كه:
(رابطهي 1)
اثبات لم
فرض كنيد حكم لم برقرار نباشد. در اين صورت A از هر يك از مجموعههاي سه عضوي ذيل حداكثر يك عضو دارد:
و چون A شامل 5 عضو است پس 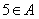 .
.
همچنين A از هر يك مجموعههاي سه عضوي ذيل حداكثر يك عضو دارد:
و در نتيجه 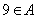 .
.
اما 4 = 5 – 9 و اين با فرض خلف در تناقض است.
همانند اثبات لم ميتوان نتيجه گرفت كه اگر X مجموعهاي شامل 13 عدد متوالي و A يك زيرمجموعهي پنج عضوي X باشد در اين صورت: 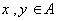 وجود دارند بهطوري كه:
وجود دارند بهطوري كه:
حال فرض كنيد:
در اين صورت مجموعهي 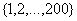 به پانزده زيرمجموعهي 13 عضوي
به پانزده زيرمجموعهي 13 عضوي 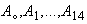 و يك زيرمجموعهي پنج عضوي
و يك زيرمجموعهي پنج عضوي 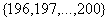 افراز ميشود.
افراز ميشود.
حال از 70 عدد كه در S قرار دارند بنا به «اصل لانهي كبوتري» حداقل پنج عدد در يكي از 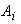 ها قرار دارند و لذا بنا به مطلب قبل، حكم مسأله نتيجه ميشود.
ها قرار دارند و لذا بنا به مطلب قبل، حكم مسأله نتيجه ميشود.