توابع با ويژگيهاي خاص ... سؤال همراه با جواب
 سؤال
سؤال
فرض كنيد كه I مجموعهي «اعداد صحيح نامنفي» و R مجموعهي «اعداد حقيقي» باشد. همهي توابع 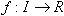 را بيابيد، بهطوري كه براي هر
را بيابيد، بهطوري كه براي هر 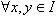 داشته باشيم:
داشته باشيم:


چنانچه 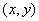 بهترتيب برابر
بهترتيب برابر 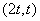 ،
، 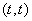 و
و 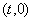 باشد چنين بهدست ميآيد:
باشد چنين بهدست ميآيد:
(رابطهي 1)
(رابطهي 2)
(رابطهي 3)
با جايگذاري 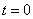 در رابطهي 3 خواهيم داشت:
در رابطهي 3 خواهيم داشت:
(رابطهي 4)
با مقايسهي رابطههاي 2، 4 و 3 داريم:
(رابطهي 5)
بنابراين از رابطهي 5 و 1 نتيجه ميشود:
(رابطهي 6)
لذا از 2 و 4 نتيجه ميشود:
(رابطهي 7)
لذا تنها «تابع ثابت صفر» در شرايط مسأله صدق ميكند.