|
اين مسأله را كليتر حل ميكنيم.
اگرچه خارج از فرض است ولي فرض ميكنيم نقاط 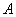 ، ، .gif) ، ، .gif) و و .gif) بر روي يك صفحه قرار دارند. اگر بر روي يك صفحه قرار دارند. اگر .gif) يك چهارضلعي محدب باشد در صورت برابري زاويههاي مقابل، چهارضلعي مذكور «متوازيالاضلاع» بوده و اضلاع مقابل با يكديگر برابر خواهند بود. در نتيجه رابطهي 2 برقرار خواهد بود. يك چهارضلعي محدب باشد در صورت برابري زاويههاي مقابل، چهارضلعي مذكور «متوازيالاضلاع» بوده و اضلاع مقابل با يكديگر برابر خواهند بود. در نتيجه رابطهي 2 برقرار خواهد بود.
اما اگر .gif) چهارضلعي محدب باشد رابطهي چهارضلعي محدب باشد رابطهي .gif) نشان ميدهد نقاط نشان ميدهد نقاط 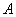 ، ، .gif) ، ، .gif) و و .gif) بر روي يك دايره قرار ميگيرد و بنابراين داريم: بر روي يك دايره قرار ميگيرد و بنابراين داريم:
(رابطهي 3)
در اين حالت مطمئناً رابطههاي ذيل برقرار نخواهد بود:
(رابطهي 4)
اگر از زواياي .gif) كسينوس بگيريم خواهيم داشت: كسينوس بگيريم خواهيم داشت:
(رابطهي 5)
بنابراين خواهيم داشت:
(رابطهي 6)
بهطور مشابه اگر از زواياي .gif) كسينوس بگيريم خواهيم داشت: كسينوس بگيريم خواهيم داشت:
(رابطهي 7)
و بنابراين رابطهي ذيل حاصل ميشود:
(رابطهي 8)
اگر .gif) ، ، .gif) و و .gif) را بهصورت ذيل تعريف كنيم: را بهصورت ذيل تعريف كنيم:
(رابطهي 9)
و رابطهي 9 را در رابطههاي 6، 7 و 8 قرار دهيم خواهيم داشت:
(رابطهي 10)
در رابطههاي 10 اگر هر يك از مقادير .gif) يا يا .gif) برابر «صفر» باشد ديگري نيز «صفر» خواهد بود. برابر «صفر» باشد ديگري نيز «صفر» خواهد بود.
اما اگر .gif) و و .gif) برابر «صفر» باشند و داشته باشيم: برابر «صفر» باشند و داشته باشيم:
(رابطهي 11)
بنابراين خواهيم داشت:
(رابطهي 12)
از سوي ديگر اگر نه .gif) نه نه .gif) برابر «صفر» نباشند نتيجه خواهيم گرفت: برابر «صفر» نباشند نتيجه خواهيم گرفت:
(رابطهي 13)
و در نتيجه خواهيم داشت:
(رابطهي 14)
بنابراين خواهيم داشت:
|
- .gif) |
|
يا |
|
- .gif) |
در هر حالت از قضيهي «پتولمي» (Ptolemy's Theorem) استفاده ميكنيم.
استفاده از اين قضيه نشان ميدهد كه:
اما اگر فرض شود نقاط 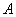 ، ، .gif) ، ، .gif) و و .gif) بر روي يك صفحه قرار نداشته باشند بنابراين لازم است رابطهي 4 برقرار باشد. بر روي يك صفحه قرار نداشته باشند بنابراين لازم است رابطهي 4 برقرار باشد. |