|
با توجه به فرض مسأله داريم:
(رابطهي 5)
بنابراين بنابر اصل «فيثاغورث» داريم:
(رابطهي 6)
لذا ميتوان مساحت مثلث 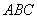 را محاسبه كرد: را محاسبه كرد:
(رابطهي 7)
از طرفي داريم:
(رابطهي 8)
با استفاده از «قضيهي نيمسازها» (Bisector Theorem) خواهيم داشت:
(رابطهي 9)
(رابطهي 10)
بدينترتيب با تعيين مساحت مثلثهاي .gif) ، ، .gif) ، ، .gif) و و .gif) به روابط ذيل دست مييابيم: به روابط ذيل دست مييابيم:
(رابطهي 11)
بنابراين مساحت چهارضلعي .gif) از رابطهي ذيل بهدست خواهد آمد: از رابطهي ذيل بهدست خواهد آمد:
|