|
هدف ما از اين زنگ تفريح افزايش آگاهي مخاطبين در حوزهي شناختي است. بدينمنظور ابتدا تعريفي از يكي از روشهاي استدلال در رياضي با عنوان «استقرا» ارائه مي كنيم.
سپس از دانشمنداني نام ميبريم كه اثبات و استفاده از «استقرا» به آنان نسبت داده ميشود. در قسمت پاياني، مثالهايي از كاربرد «استقراي رياضي» بيان خواهيم كرد.
«استقراي رياضي» روشي براي استدلال رياضي است كه بهخصوص در مواردي بهكار ميرود كه يك عبارت مفروض براي تمام «اعداد طبيعي» صدق ميكند. اين روش ميتواند براي اثبات جملههايي در ساختارهاي عمومي كاملاً منطقي بهكار رود.
چنين تعميمهايي - كه اصطلاحاً «استقراي ساختاريافته» (Structural Induction) ناميده ميشود - در «منطق رياضي» (Mathematical Logic) و علوم كامپيوتر استفاده ميشود.
بهعلاوه مفهوم «استقراي رياضي» از لحاظ منطقي معادل مفهوم «خوشترتيبي» (Well Ordering) است.
نسبت به «استقراي رياضي» نبايد اينگونه تعبير نامناسبي انجام شود كه مثلاً: داراي استحكام لازم نبوده و با رياضي تطبيق ندارد. در واقع «استقرا» در رياضي، شكلي از «استدلال قياسي» (Deductive Reasoning) بوده و بهشدت مستحكم است.
گفته ميشود اولين كاربرد «استقراي رياضي» به دو دانشمند بهنامهاي ذيل برميگردد:
اولين اثبات «استقراي رياضي» نيز در بعضي از منابع به «ابوبكر ابن الحسين» معروف به «الكرجي» حدود 1000 سال بعد از ميلاد نسبت داده شده است؛ زماني كه از «استقرا» براي اثبات «قضيهي چند جملهايها»، «مثلث پاسكال» و «مكعبهاي اعداد صحيح» استفاده كرد. اين دانشمند در اثباتش از دو جزو از يك اثبات استقرايي يعني: «صحت جمله براي 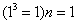 » و «نتيجهگيري درستي » و «نتيجهگيري درستي .gif) از از .gif) » استفاده كرد. » استفاده كرد.
پس از آن، دانشمند شهير ايراني «ابن هيثم» (الهازن) از روش استقرايي و تعميم براي اثبات موارد ذيل بهعنوان نتيجهي مهم از «حساب انتگرال» (Integral Calculus) استفاده كرد:
|
- جمع توانهاي چهارم اعداد صحيح |
|
- جمع همهي توانهاي اعداد صحيح. |
اگرچه وي تنها آن را براي اعداد صحيح بهخصوصي ثابت كرد اما در اثباتش در مورد آن اعداد صحيح، از «استقرا» و تعميمپذيري استفاده كرد.
رياضيدان قرن دوازدهم «السموئل ابن يحيي مغربي» امروزيترين اثبات «استقرا» را انجام داد. وي از بسط اثبات «قضيهي چندجملهايها» و «مثلث پاسكال» - كه قبلاً «الكرجي» بيان كرده بود – استفاده كرد. بحث استقراي «السموئل» تنها مرحلهاي كوتاه از اثبات كامل استقرايي «قضيهي چندجملهايهاي عمومي» محسوب ميشود.
اما به هر حال هيچكدام از دانشمندان قديمي مذكور بهوضوح «فرض استقرا» را توضيح ندادند. اولين اثبات واضح و روشن «استقرا» در سال 954 (1575 ميلادي) توسط رياضيدان و منجم ايتاليايي «فرانسيسكو مائوروليكو» (Francesco Maurolico) انجام شد. اين دانشمند از اين روش براي اثبات اينكه جمع .gif) عدد صحيح و فرد برابر عدد صحيح و فرد برابر .gif) است استفاده كرد. است استفاده كرد.
همچنين شرط استقرا بهطور مستقل توسط دانشمندان ذيل كشف شد:
«استقراي رياضي» براي اثبات اين امر بهكار ميرود كه هر جمله از يك دنبالهي نامحدود از آن تبعيت ميكند. اينكار در دو مرحله انجام ميشود:
|
- اثبات اينكه عبارت اول در دنبالهي نامحدود مذكور از آن تبعيت ميكند. |
|
- اثبات اينكه چنانچه جملهاي در دنبالهي نامحدود نيز از آن پيروي كند جملهي بعدي نيز از آن تبعيت خواهد كرد. |
تعريف ساده و عمومي از «استقراي رياضي» عبارت است از: اثبات اينكه يك جمله براي تمام اعداد طبيعي .gif) صادق بوده و شامل دو مرحله است: صادق بوده و شامل دو مرحله است:
|
- مرحلهي اصلي
نشان دادن اينكه جمله بهازاي .gif) صادق است. صادق است. |
|
- مرحلهي استقرايي
نشان دادن اينكه اگر جمله بهازاي .gif) صادق باشد بهازاي صادق باشد بهازاي .gif) نيز صادق خواهد بود. نيز صادق خواهد بود. |
در استقرا، جملهاي كه بعد از كلمهي «اگر» آمده است (جمله بهازاي .gif) صادق باشد) اصطلاحاً «فرض استقرا» ناميده ميشود. صادق باشد) اصطلاحاً «فرض استقرا» ناميده ميشود.
بدينترتيب ابتدا اثبات ميشود «فرض استقرا» صادق است (جمله بهازاي .gif) صادق است) و سپس از اين فرض براي اثبات صدق جمله براي صادق است) و سپس از اين فرض براي اثبات صدق جمله براي .gif) نيز استفاده ميشود. نيز استفاده ميشود.
در اينجا توجه به پديدهي معروف با عنوان «اثر دومينو» (Domino Effect) براي درك هرچه بيشتر «استقرا» بسيار مفيد است. «دومينو» عبارت است از يك رديف طولاني از قطعههاي مكعبي كه از سطح قاعده بر روي زمين قرار گرفتهاند:
|
- اولين «دومينو» سرنگون ميشود. |
|
- هر زمان كه يك «دومينو» ميافتد «دومينوي» مجاور آن نيز سرنگون ميشود. |
بدينترتيب شما ناظر افتادن همهي «دومينوها» خواهيد بود و اين واقعيت ناگزير و حتمي است.
در نظر بگيريد يك رديف از برگهاي گلهاي برگپهن در بركهاي بر روي سطح آب قرار دارد. اگر قورباغهاي بخواهد از اين بركه عبور كند بايد:
|
- تعيين كند كه آيا برگ اولي تحمل وزن وي را دارد. |
|
|
- ثابت نمايد كه ميتواند از يك برگ بر روي برگ ديگر بپرد. |
در اين صورت است كه شما نتيجه خواهيد گرفت كه وي مي تواند از روي همهي برگها بپرد.
«فرانسيسكو مائوروليكو» (Francesco Maurolico) در 31 تير سال 873 (21 ژولاي 1494 ميلادي) در «مسيناي ايتاليا» بهدنيا آمد. در تمام طول عمرش به فعاليت در حوزههاي: هندسه، فيزيك نور، مكانيك، موسيقي و نجوم پرداخت. پدر و مادر وي يوناني بودند كه پس از سقوط «قسطنطنيه» در سال 832 (1453 ميلادي) در شهر «سيسيل» ايتاليا سكونت داشتند.
«فرانسيسكو مائوروليكو» آموزشي سختي ديد؛ پدرش فيزيكدان بود كه بعداً در شهر «مسينا» بهسمت سرپرست ضرابخانه منصوب شد. خانوادهاش داراي ويلايي در خارج شهر بودند.
در سال 900 (1521 ميلادي) به تحصيل علوم ديني پرداخته و در سال 929 (1550 ميلادي) راهبه شد.
«فرانسيسكو مائوروليكو» (Francesco Maurolico) همانند پدر بهسمت سرپرست ضرابخانهي «مسينا» منصوب شد. بين سالهاي 927 تا 929 (1548 تا 1550 ميلادي) در «قلعهي پولينا» به رصد پرداخت.
در سال 948 (1569 ميلادي) بهسمت پروفسور «دانشگاه مسينا» منصوب شد.
مهمترين فعاليتهاي اين دانشمند را ميتوان در چند زمينه خلاصه كرد:
|
- انعكاس نور
تمركز فعاليتهاي «فرانسيسكو مائوروليكو» (Francesco Maurolico)، «انعكاس نور» بود و بدينترتيب تلاش كرد توضيحي براي پديدهي «رنگين كمان» بيابد.
نتيجهي اين فعاليتها در سال 990 (1611 ميلادي) و پس از مرگش منتشر شد.
وي همچنين «اتاق تاريك» را مطالعه كرده است.
|
|
- اثبات استقراي رياضي
در سال 954 (1575 ميلادي) «استقراي رياضي» را اثبات كرد.
|
|
- مركز ثقل
در همان سال (954 يا 1575 ميلادي) تلاش كرد مركز ثقل اجسام (هرمها، اشكال سهموي و ...) را بيابد.
|
|
- تاريخ شهر «سيسيل»
تاريخ شهر «سيسيل» را همراه با شرح زندگي خود مكتوب كرد. وي با حقوق 100 سكه طلا در سال از طرف مجلس سناي سيسيل مأموريت يافت طي دو سال اين كتاب خود را بههمراه تحقيقهايش در رياضيات كامل كند.
|
|
- انتشار كتاب
كتابي با عنوان «گيتاشناسي» منتشر كرد كه در آن به روششناسي (Methodology) اندازهگيري زمين پرداخت كه بعداً (در سال 1049 يا 1670 ميلادي) توسط محققي بهنام «جين پيكارد» (Jean Picard) براي اندازهگيري نصفالنهار از آن استفاده شد.
«فرانسيسكو مائوروليكو» (Francesco Maurolico) نسخهاي از كتاب «مشكلات مكانيكي ارسطو» را منتشر كرد؛ همچنين در زمينهي موسيقي داراي كتاب است. كتابهاي ديگري نيز از وي منتشر شده است.
وي همچنين نقشهاي از شهر «سيسيل» تهيه و در سال 954 (1575 ميلادي) منتشر كرد.
|
|
- «فرانسيسكو مائوروليكو» (Francesco Maurolico) دستنوشتههاي قديمي دانشمنداني نظير ذيل را ترجمه كرد:
|
اين دانشمند در اول مرداد 954 (1575 ميلادي) در شهر «مسينا» دار فاني را وداع گفت. براي قدرداني از اين دانشمند، حفرههاي ماه بهنام وي «مائوروليكوس» (Maurolycus) ناميده شده است.
از «استقرا» استفاده كرده و رابطههايي نظير ذيل را ثابت ميكنيم:
(رابطهي 1)
(رابطهي 2)
(رابطهي 3)
(رابطهي 4)
(رابطهي 5)
رابطهي 1 را براي .gif) بررسي ميكنيم: بررسي ميكنيم:
(رابطهي 6)
اگر .gif) در اينصورت داريم: در اينصورت داريم:
(رابطهي 7)
اگر .gif) ثابت ميكنيم: ثابت ميكنيم:
(رابطهي 8)
با جايگذاري در رابطهي 1 خواهيم داشت:
(رابطهي 9)
بدينترتيب رابطهي 8 ثابت ميشود.
تابعي نظير .gif) را بهصورت ذيل تعريف ميكنيم: را بهصورت ذيل تعريف ميكنيم:
(رابطهي 10)
ابتدا ثابت ميكنيم رابطهي 2 براي .gif) صادق است يعني داريم: صادق است يعني داريم:
(رابطهي 11)
بديهي است كه داريم:
(رابطهي 12)
از طرفي ميدانيم:
(رابطهي 13)
با مقايسهي رابطههاي 12 و 13 داريم:
(رابطهي 14)
بدينترتيب رابطهي 2 (يا 11) صادق است.
سپس اثبات ميكنيم اگر رابطهي 2 براي .gif) صادق باشد يعني اگر رابطهي 15 را داشته باشيم آنگاه رابطهي 16 نيز صادق است: صادق باشد يعني اگر رابطهي 15 را داشته باشيم آنگاه رابطهي 16 نيز صادق است:
(رابطهي 15)
(رابطهي 16)
براي اين منظور در رابطهي 10، .gif) را برابر را برابر .gif) قرار ميدهيم؛ در اين صورت داريم: قرار ميدهيم؛ در اين صورت داريم:
(رابطهي 17)
با جايگذاري رابطهي 16 در 17 خواهيم داشت:
(رابطهي 18)
بدينترتيب رابطهي 16 ثابت ميشود.
تابع .gif) را بهصورت ذيل تعريف مي كنيم: را بهصورت ذيل تعريف مي كنيم:
(رابطهي 19)
ابتدا ثابت ميكنيم رابطهي 3 براي .gif) صادق است: صادق است:
(رابطهي 20)
براي اين منظور .gif) را بهدست ميآوريم: را بهدست ميآوريم:
(رابطهي 21)
از طرفي .gif) را محاسبه ميكنيم: را محاسبه ميكنيم:
(رابطهي 22)
بدينترتيب رابطهي 19 براي .gif) صادق خواهد بود. صادق خواهد بود.
سپس ثابت ميكنيم اگر رابطهي 3 براي .gif) صادق باشد براي صادق باشد براي .gif) نيز صدق ميكند. نيز صدق ميكند.
اگر رابطهي 3 براي .gif) صادق باشد خواهيم داشت: صادق باشد خواهيم داشت:
(رابطهي 23)
اگر .gif) باشد در اين صورت خواهيم داشت: باشد در اين صورت خواهيم داشت:
(رابطهي 24)
با جايگذاري رابطهي 23 در 24 خواهيم داشت:
(رابطهي 25)
با جايگذاري رابطهي 23 در 25 خواهيم داشت:
(رابطهي 26)
بديهي است كه طرف راست رابطهي 26 برابر است با: .gif) . .
بدينترتيب رابطهي 3 ثابت شد.
بههمين طريق ميتوانيد رابطههاي 4 و 5 را ثابت كنيد. منتظر جوابهاي شما هستيم.
|