|
|
 |
|
شكل 1. |
پف فيلي بخريد! بر روي صندلي سينما بنشينيد! راحت لم بدهيد! حال بياييم افراد و چيزهايي كه نقشهاي اصلي را در فيلم دارند، بررسي كنيد ...
اين جملههايي است كه رياضيداني بهنام «ژوان ليزنبي» (Joan Lasenby) مطلب جالب ذيل را با آن آغاز كرده است كه براي «زنگ تفريح» انتخاب كردهايم. «ژوان ليزنبي» (Joan Lasenby) رياضيات را در «ترينيتي كالج كمبريج» (Trinity College Cambridge) آغاز كرد. سپس دورهي «دكتري» (PhD) را در دپارتمان فيزيك - گروه «نجوم راديويي» (Radio Astronomy) ادامه داد.
پس از دورهي كوتاهي كه براي يك شركت فعاليت صنعتي انجام ميداد به فعاليتهاي دانشگاهي بازگشت و هماكنون يك مدرس دانشگاهي در «گروه فرايندهاي سيگنالي» (Signal Processsing Group) از «دپارتمان مهندسي كمبريج» (Cambridge University Engineering)، يك عضو و مدير پژوهشي در «كالج ترينيتي» (Trinity College) است.
علايق پژوهشي وي در حوزهي «تصاوير كامپيوتري» (Computer Vision)، «گرافيك كامپيوتري» (Computer Graphics)، «فرايندسازي تصاوير» (Image Processing)، «ضبط تصوير» (Image Processing)، «ضبط حركت» (Motion Capture) و «جبر هندسي» (Geometric Algebra) است.
|

|
|
شكل 2 - «ژوان ليزنبي» (Joan Lasenby). |
|
رياضيات با افتخار تقديم ميكند ... | همهي ما از تصاوير كامپيوتري – كه بهطور باورنكردني شبيه به دنياي واقعي هستند – متعجب ميشويم. آنچه اغلب ما نميفهميم آن است كه دايناسورهاي «پارك ژوراسيك» و موارد اعجابانگيز فيلم «ارباب حلقهها» [بهخصوص تغيير شكلهاي «غلام» (Golum)] بدون «رياضيات» ميسر نميشود.
اما چگونه تصاوير اعجابانگيز ساخته ميشوند؟ گرافيك و تصاوير مجازي كامپيوتري، موضوعهاي مهمي تلقي ميشوند. قصد داريم نگاه سادهاي به رياضياتي بياندازيم زيرا كه ما را به ايجاد محصول نهايي رهنمون ميكند. ابتدا دنيايي را خلق ميكنيم كه در فيلمها ديده ميشود؛ سپس آن را با زندگي تطبيق ميدهيم.
|
|
|
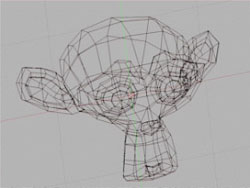
شكل 3 – ابتدا اشيا با اسكلتهاي سيمي
مدل ميشوند كه از چندضلعيهاي ساده
نظير: «مثلث» تشكيل شدهاند. |
اولين مرحله در خلق يك فيلم توليدي كامپيوتري، ايجاد شخصيتهاي داستاني و دنيايي است كه آنها در آن زندگي ميكنند. هركدام از اين اشيا بهصورت صفحههايي طراحي ميشوند كه از «چندضلعيهاي» بههم متصل (بهخصوص «مثلثها») تشكيل شدهاند.
رؤوس هر مثلث در حافظهي كامپيوتر ذخيره ميشوند. چيزي كه اهميت دارد آن است كه بدانيم كدام وجه مثلث، بيرون شيء يا شخصيت مورد نظر است.
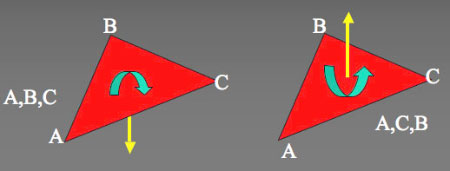
اين اطلاعات بهصورت رمز آورده ميشوند (Encode) تا رؤوس را بر «قانون دست راست» ذخيره كنند. انگشتان دست خود را در اطراف مثلث خم كنيد تا به رؤوس آن برسيد. تنها يك راه براي اينكار وجود دارد و انگشتانتان به يك ضلع مثلث منتهي ميشود كه اين ضلع وجه خارجي آن است.
اگر سعي كنيد بهطور مثال اين امر را عملي كنيد ميفهميد كه جهت خارجي [بهنام «عمود خارجي» (Outward Normal)] مربوط به مثلث 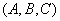 در خلاف جهت مثلث در خلاف جهت مثلث .gif) است. است.
|
|
|
شكل 4 – خط عمود خارجي 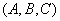 در جهت خلاف جهت مثلث در جهت خلاف جهت مثلث .gif)
مطابق با «قانون دست راست» است. |
اكنون سطح شيء مورد نظر را مجموعهاي از شبكههاي فلزي از مثلثها باشد ميتوانيم هر جزو آن را رنگ كنيم.
در اينجا مهم است كه بهطور واقعي از نورپردازي صحنههايي عكسبرداري كنيم كه ميخواهيم مدل كنيم. اين كار با استفاده از فرايندي بهنام «رديابي پرتوي» (Ray Tracing) انجام ميشود.
با شروع از نقطهي ديد ما، پرتوهايي را رديابي ميكنيم كه بهسمت شيء مورد نظر تابانده ميشود:
|
- اگر پرتوها از چشم ما بهسمت رويهها (يكي از مثلثهاي شبكهي فلزي) منعكس شود و با منبع نوراني برخورد كرده آن رويه را با يك رنگ روشن، سايه ميدهيم بهگونهاي كه نشاندهندهي پرتوافكني منبع نوراني باشد. |
|
- اگر پرتو منعكس شده، به منبع نوراني برخورد نكند رويه را با رنگي تيرهتر، رنگ ميكنيم. |
|
|
|
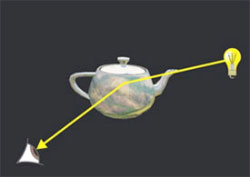
شكل 5 – يك پرتو از ديد ما به يك رويه
را رديابي كنيد. آيا پرتو مذكور
منعكس نشده و به يك منبع نوراني
برخورد ميكند؟ |
براي رديابي پرتوي كه به رويهاي بهخصوص بازميگردد نياز به توضيح رياضي «سطح» داريم و معادلههاي هندسي را در آن پرتو و «سطح» – كه توسط آن رويه توصيف ميشود – حل ميكنيم. اين عمليات توسط «بردارها» (Vectors) انجام ميشود.
يك دستگاه مختصات سهبعدي در مبدأ مختصات [نقطهي .gif) ] در صحنهي مورد نظرمان در نقطهي ديد ما قرار ميگيرد. اكنون يك بردار ] در صحنهي مورد نظرمان در نقطهي ديد ما قرار ميگيرد. اكنون يك بردار .gif) جهت شروع از مبدأ را مشخص كرده و به نقطهاي با مختصات جهت شروع از مبدأ را مشخص كرده و به نقطهاي با مختصات .gif) ، ، .gif) و و .gif) منتهي ميكنيم. منتهي ميكنيم.
ميتوانيم را در يك عدد مثل 2 بدينترتيب ضرب كنيم:
بنابراين .gif) پيكاني است همجهت با بردار پيكاني است همجهت با بردار .gif) اما داراي طولي دو برابر آن. اما داراي طولي دو برابر آن.
اكنون به عبارت .gif) توجه كنيد كه در آن توجه كنيد كه در آن .gif) يك متغير است؛ بهعبارت ديگر عددي «حقيقي» است؛ بيانگر پيكاني با طول معين است بنابراين نهتنها «طول» بلكه «جهت» هم متغير محسوب ميشود؛ بهعبارت ديگر، عبارت مذكور بيانگر خطي است كه شامل بردار يك متغير است؛ بهعبارت ديگر عددي «حقيقي» است؛ بيانگر پيكاني با طول معين است بنابراين نهتنها «طول» بلكه «جهت» هم متغير محسوب ميشود؛ بهعبارت ديگر، عبارت مذكور بيانگر خطي است كه شامل بردار .gif) است يعني بيانگر خطي مستقيم (يعني «پرتوي») است كه از مبدأ («نقطهي ديد ما») آغاز شده و همجهت با بردار است يعني بيانگر خطي مستقيم (يعني «پرتوي») است كه از مبدأ («نقطهي ديد ما») آغاز شده و همجهت با بردار .gif) است. است.
صفحهي تعريف شده توسط «رويهي مثلثي شكل» ميتواند با سه نوع داده بيان شود:
رابطههاي ذيل بيانگر روابط مربوط به يك پرتو است كه از چشم ما آغاز و به صفحهي نشان داده شده با يك رويه ختم ميشود. براي درك چگونگي و محل تلاقي پرتو مذكور با رويه و محاسبهي روابط پرتو منعكس شده، نياز به حل معادلههاي مربوط به آن هستيم.
معادلهي يك پرتو كه در آن .gif) عددي «حقيقي» و عددي «حقيقي» و .gif) يك «بردار» است بهصورت ذيل نوشته ميشود: يك «بردار» است بهصورت ذيل نوشته ميشود:
(رابطهي 1)
معادلهي صفحهي نشان داده شده با يك «رويه» همراه با رؤوس .gif) ، ، .gif) و و .gif) عبارت است از [1]: عبارت است از [1]:
(رابطهي 2)
رديابي پرتوها ميتواند صحنههايي واقعي اما خيلي كُند بيافريند. اين امر براي فيلمهاي ساخته شده توسط كامپيوتر پذيرفتني است اما زماني كه به تكنيكهاي نورپردازي در صحنههاي واقعي نياز باشد (مانند: بازيهاي كامپيوتري) امري مشكل محسوب ميشود.
مدل كردن ديناميك مفاهيم پيچيده نظير: سايهها، جلوههاي ويژه و انعكاسهاي چندگانه سخت بوده و در اين موارد، روشهاي رياضي پيچيدهتري نيازمند است؛ روشهايي نظير: «انتقال پرتوهاي پيش محاسبه شده» (Recomputed Radiance Transfer) و «راديوسيتي» [2].
|

|
|
الف. |
|
|

|
|
ب. |
|
شكل 6 – بازيهاي كامپيوتري مانند:
«دوم 3» (Doom 3) و «شبهايي كه
هرگز زمستاني نيست» (Neverwinter Nights)
نياز به نورپردازي ديناميك دارد. |
|
آنچه پنداشته ميشود كمي تخيل است | اولين بار كه صحنهي مورد نظر تنظيم ميشود ما منتظر كارگردان ميمانيم تا فرياد براورد: «حركت!» (!Action)؛ بدينترتيب شخصيتهاي فيلم شروع به حركت ميكنند. اكنون ما رياضياتي را مورد آزمايش قرار ميدهيم كه ميتوانند تصاوير را به زندگي ما بياوردند.
يكي از اولين حركتهاي اساسياي كه يك شيء ميتواند اجرا كند چرخش دور يك محور و زاويهي داده شده است. «هندسهي مختصاتي» (Coordinate Geometry) ابزاري براي محاسبهي موقعيت هر نقطه در شيء زماني است كه دوران ميكند. اما در عين حال ابزاري مؤثر و سريع محسوب نميشود.
براي يافتن چنين ابزاري اجازه دهيد يك مرحله به قبل بازگرديم يعني به كلاس رياضي. ميدانيم براي 25 دو ريشهي درجهي دوم وجود دارد:
|
- .gif) |
|
- .gif) |
بهگونهاي كه داشته باشيم:
اما ريشهي دوم عدد .gif) چيست؟ چيست؟
براي يافتن ريشهي دوم اعداد منفي، رياضيدانان مجبورند عددي جديد بهنام خلق كنند بهگونهاي كه داشته باشيم:
سپس از آنجايي كه داريم:
رابطهي ذيل را درمييابيم:
با مقدمهاي كه در مورد .gif) گفته شد در مييابيم كه معادلههايي شبيه به گفته شد در مييابيم كه معادلههايي شبيه به .gif) اكنون حلشدني هستند. همچنين اعدادي بهشكل اكنون حلشدني هستند. همچنين اعدادي بهشكل .gif) - كه عدد «مختلط» (Complex) ناميده ميشوند – ابزاري مهم در رياضيات محسوب ميشوند. اما بسياري از مردم با عدد جديد، عجيب و موهومي - كه عدد «مختلط» (Complex) ناميده ميشوند – ابزاري مهم در رياضيات محسوب ميشوند. اما بسياري از مردم با عدد جديد، عجيب و موهومي .gif) ارتباط برقرار نميكنند. ارتباط برقرار نميكنند.
نهايتاً در سال 1184 (1806 ميلادي)، رياضيداني آماتور بهنام «جين رابرت آرگاند» (Jean Robrt Argand) تفسيري هندسي از اعداد «مختلط» و عدد «موهومي» (Imaginary) .gif) ارائه داد. «آرگاند» (Argand) اعداد «مختلط» را با نقاطي در صفحه نشان داد بهگونهاي كه: ارائه داد. «آرگاند» (Argand) اعداد «مختلط» را با نقاطي در صفحه نشان داد بهگونهاي كه:
|
- عدد «حقيقي» 1 بر روي يك محور |
|
- و عدد «موهومي» .gif) بر روي محور ديگر بر روي محور ديگر |
قرار گرفته است.
بهعنوان مثال:
عدد .gif) به نقطهي به نقطهي .gif) نسبت داده ميشود. نسبت داده ميشود.
معمولاً يك عدد «مختلط» .gif) به نقطهي به نقطهي .gif) منتسب ميشود. منتسب ميشود.
|
|
|
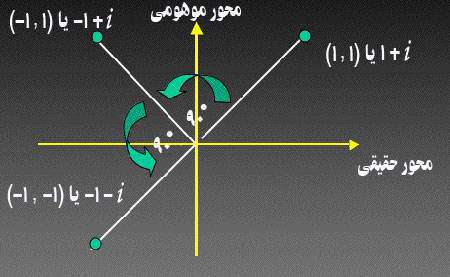
شكل 7 – ضرب اعداد «مختلط»
داراي توصيفي هندسي است: «دوران» (Rotation). |
«آرگاند» (Argand) فهميد كه ضرب اعداد «مختلط» داراي توصيفي هندسي است كه آن عبارت است از: «دوران» (Rotation). اجازه دهيد به آنچه در اثر ضرب عدد .gif) - كه با نقطهي - كه با نقطهي .gif) نشان داده ميشود – در عدد نشان داده ميشود – در عدد .gif) اتفاق ميافتد نگاهي داشته باشيم: اتفاق ميافتد نگاهي داشته باشيم:
(رابطهي 3)
عدد بهدست آمده با نقطهي .gif) نشان داده شده كه در واقع دوراني 90 درجهاي نسبت به نقطهي نشان داده شده كه در واقع دوراني 90 درجهاي نسبت به نقطهي .gif) محسوب ميشود. محسوب ميشود.
اگر نتيجهي حاصل را در .gif) مجدداً ضرب كنيم خواهيم داشت: مجدداً ضرب كنيم خواهيم داشت:
(رابطهي 4)
عدد .gif) نشاندهندهي نقطهي نشاندهندهي نقطهي .gif) است كه دوران 90 درجهاي دوبارهي نقطهي است كه دوران 90 درجهاي دوبارهي نقطهي .gif) محسوب ميشود. محسوب ميشود.
بنابراين ضرب كردن در عدد .gif) بهمعني «دوران 90 درجهاي» است. در واقع، هر دوراني نهتنها دوران 90 درجهاي ميتواند با استفاده از ضرب در يك عدد «مختلط» بهدست آيد. بهمعني «دوران 90 درجهاي» است. در واقع، هر دوراني نهتنها دوران 90 درجهاي ميتواند با استفاده از ضرب در يك عدد «مختلط» بهدست آيد.
|

|
|
شكل 8 – «سر ويليام روان هاميلتون»
(Sir William Rowan Hamilton). |
رياضيداني بهنام «سر ويليام روان هاميلتون» (Sir William Rowan Hamilton) شايد مشهورترين فرد در دانشگاه «ترينيتي» شهر «دوبلين» (Trinity College Dublin) باشد. وي دههي آخر زندگياش را در جستجوي راهي براي بيان دورانهاي سهبعدي در وضعيتي مشابه با اعداد «مختلطي» صرف كرد كه ميتواند «دورانهاي دوبعدي» را بيان ميكند.
«هاميلتون» (Hamilton) در انتهاي عمرش جوابي را كشف كرد كه در آن اعداد بهشكل ذيل هستند كه بهنام «چهارگان» (Quaternions) خوانده ميشوند:
(رابطهي 5)
كه در آن داريم:
(رابطهي 6)
همچنين اعداد .gif) «حقيقي» محسوب ميشوند. «حقيقي» محسوب ميشوند.
اعداد «چهارگان» (Quaternions) - همانند آنچه در مورد اعداد «مختلط» گفته شد – بهصورت هندسي قابل توصيف بوده و براي بيان آن از «دوران» (Rotation) استفاده ميشود. اما در آن بهجاي دوبعد، دوران در فضاي سهبعدي انجام ميشود.
براي اين منظور .gif) ، ، .gif) و و .gif) بيانگر صفحههاي «اصلي» (Elemental) در فضاي سهبعدي هستند؛ به اين معنا كه بيانگر صفحههاي «اصلي» (Elemental) در فضاي سهبعدي هستند؛ به اين معنا كه .gif) ، ، .gif) و و .gif) بهترتيب بيانگر صفحههاي بهترتيب بيانگر صفحههاي .gif) ، ، .gif) و و .gif) با خط عمود خارجي بهترتيب در جهتهاي با خط عمود خارجي بهترتيب در جهتهاي .gif) ، ، .gif) و و .gif) ميباشند. ميباشند.
فرض كنيد ميخواهيم نقطهاي نظير: .gif) را با زاويهي را با زاويهي .gif) حول يك محور – كه با بردار حول يك محور – كه با بردار .gif) نشان داده ميشود – دوران دهيم. نشان داده ميشود – دوران دهيم.
دو عدد «چهارگان» (Quaternions) و را با استفاده از بردار .gif) و و .gif) زاويهي دوران زاويهي دوران .gif) با رابطههاي ذيل ايجاد ميكنيم: با رابطههاي ذيل ايجاد ميكنيم:
(رابطهي 7)
و
(رابطهي 8)
سپس ميتوانيم دو طرف رابطههاي 7 و 8 را در .gif) - كه بهعنوان تركيبي از بردار «واحد» (Unit Vector) در جهتهاي - كه بهعنوان تركيبي از بردار «واحد» (Unit Vector) در جهتهاي .gif) ، ، .gif) و و .gif) بيان ميشود - البته با پيروي از قواعد ويژهاي براي ضرب صفحههاي بيان ميشود - البته با پيروي از قواعد ويژهاي براي ضرب صفحههاي .gif) ، ، .gif) و و .gif) و بردارهاي «واحد»، ضرب كنيم. بدينترتيب رابطهي ذيل بهدست ميآيد: و بردارهاي «واحد»، ضرب كنيم. بدينترتيب رابطهي ذيل بهدست ميآيد:
(رابطهي 9)
نقطهاي كه با اين ضرب بهدست ميآيد درست همانند آن است كه محور داده شده را تحت «زاويهي داده شده» بچرخانيم.
بنابراين همانگونه كه اعداد «مختلط» ميتوانند براي توصيف «دورانها» در يك صفحه بهكار روند اعداد «چهارگان» (Quaternions) نيز ميتوانند براي توصيف «دورانها در فضاي سهبعدي» بهكار روند.
اين فكر زماني در ذهن «سر ويليام روان هاميلتون» (Sir William Rowan Hamilton) خطور كرد آنهم زماني كه زير پل «دوبلين» (Dublin) قدم ميزد؛ وي به اين نتيجه دست يافت كه مؤثرترين روش، دوران اشيا در سه بعد است. اما همه از روش ضرب جديدش خوشحال نشدند.
|

|
|
شكل 10 – «لرد كلوين» (Lord Kelvin). |
فيزيكدان مشهور «لرد كلوين» (Lord Kelvin) دربارهي اعداد «چهارگان» (Quaternions) ميگويد: «... با وجود ابتكار زيبايي كه انجام شده است براي افرادي كه با اين مسأله در تماس قرار بگيرند شديداً نامطلوب بهنظر ميرسد»!
بهخصوص با وجود برخي نگرانيها، اين واقعيتي است كه وقتي دو عدد «چهارگان» (Quaternions) را در هم ضرب ميكنيد جواب به «شيوهاي» بستگي دارد كه آنها را در هم ضرب ميكنيد ويژگياي كه «ناجابهجايي» (Non Commutativity) ناميده ميشود.
بهعنوان مثال:
از قواعد ضرب «هاميلتوني» (Hamilton's Multiplication) ميتوان روابط ذيل را نشان داد:
(رابطهي 10)
(رابطهي 11)
اما بههر حال ميتوان نشان داد وقتي فرد بر روي .gif) ، ، .gif) و و .gif) بهعنوان صفحههاي «اصلي» (Elemental) عمل ميكند ويژگيهايي كه اينچنين از نظر «كلوين» (Kelvin) و دانشمندان همعصر وي نگرانكننده بودند بهطور مستقيم از رياضيات آن زمان نشأت ميگرفت. بهعنوان صفحههاي «اصلي» (Elemental) عمل ميكند ويژگيهايي كه اينچنين از نظر «كلوين» (Kelvin) و دانشمندان همعصر وي نگرانكننده بودند بهطور مستقيم از رياضيات آن زمان نشأت ميگرفت.
|
|
|
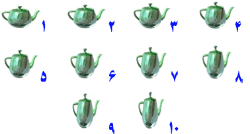
شكل 11 – شكل قوري چايخوري
بهتدريج در طي يك مجموعه فريم تغيير ميكند. |
ابتكار «هاميلتون» (Hamilton) امروزه در بسياري از كاربردهاي گرافيكي براي حركت اشيا يا ايجاد حركت بهكار ميرود. دو نوع از ابزارهاي مهم در كاربردهاي گرافيك كامپيوتري عبارتاند از:
|
- «تغيير شكلها» (Deformations) |
|
- «درونيابي» (Interpolation). |
«درونيابي» (Interpolation) و روش «تعيين چهارچوب كليدي» (Key Framing) شروع طراحي يك شيء را تعيين كرده شكل و موقعيت آن را به پايان ميبرد. مراحل مياني فعاليت طراحي توسط كامپيوتر مشخص ميشود (شكل 11).
انيميشني از يك مار با عنوان «مار اوليه» (Rudimentary Snake) توسط «ريچارد وارهام» (Richard Wareham) طراحي شده است كه در آن، تمام مار با كامپيوتر با استفاده از «درونيابي» (Interpolation) از حركت چند نقطهي مشخص شده توليد ميشود.
ياداوري - براي مشاهدهي انيميشن مذكور نياز به نرمافزار Divx داريد.
تغيير شكلها روشي براي طراحي اشياي پيچيده از انواع سادهتر آن است. پوششي كه از روي يك كرهي تغيير شكليافته برداشته ميشود ميتواند با دستكاري رياضي همان صحنه شامل يك كرهي معمولي بهدست آيد. هم دستكاريها و هم درونيابيها نياز به روشهاي رياضي پايدار و سريع و روشهاي وابسته به اعداد «چهارگان» (Quaternion) دارد كه فقط همانها را فراهم ميكند.
|

|
|
شكل 12 – فيلم «ارباب حلقهها». |
|
|

|
|
شكل 13 - «غلام» در فيلم
«ارباب حلقهها» (The Lord of the Rings). |
|
ايجاد شخصيت «غلام» (Gollum) بهصورت باوركردني (Making Gollum Believable) |
| در فيلم «ارباب حلقهها» (The Lord of the Rings) | روشهاي توصيف شدهي مذكور، ابزارهاي اساسياي براي ساخت انيميشنهاي كلاسيك بوده و اعتقاد ما ناشي از شخصيتهاي كارتوني است كه از اين طريق بهدست آمده و ما را كاملاً خوشحال ميكند. اما زماني كه اين ابزار براي انسانهاي انيميشني استفاده ميشود ميتوانيم فوراً آن را «نادرست» تلقي كنيم زيرا براي ايجاد حركت واقعبينانه، معمولاً ضبط حركت مورد نياز است.
شخصيتهاي زيادي نظير: «غلام» (Gollum) در فيلم «ارباب حلقهها» (The Lord of Rings) با استفاده از «ضبط حركت» ساخته ميشوند. اين كار با چسباندن انعكاسها به افراد واقعي در نقطههاي محوري بدن، سر، شانهها، آرنجها، زانوها و ... مربوط به آن شخصيتها انجام ميشود.
با چند دوربين از شخصيتها فيلمبرداري ميشود؛ همچنين در محل انعكاسهايي كه بر روي يك كامپيوتر ذخيره ميشود تغيير ايجاد خواهد شد. سپس با دادههاي سهبعدي تنظيم ميگردد. نهايتاً همهي روشهاي توصيف شده مذكور منتهي به گذاشتن «گوشت» بر روي استخوانها و خلق يك شخصيت در حال حركت، در حال «تنفس» و «زنده» ميشود.
|

|
|
شكل 14 - چسباندن انعكاسها به افراد واقعي
در نقطههاي محوري بدن، سر، شانهها،
آرنجها، زانوها و ... مربوط به آن شخصيتها. |
|
|

|
|
شكل 15 – دادهها از حركتهاي انعكاسهاي
چسبيده به بخشهاي مختلف بدن
ضبط ميشود. |
|
|
|
|
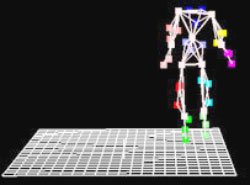
شكل 16 - يك اسكلت بهطور رياضي
با دادهها تنظيم ميشود. |
اگر تاكنون از فهرست تمام افرادي كه در تهيهي يك فيلم نقش دارند مطلع باشيم با گسترهاي متنوع از افراد با استعدادهاي خدادادي نظير موارد ذيل مواجه ميشويم:
|
- نويسندگان |
|
- كارگردانان |
|
- هنرمندان |
|
- طراحان لباس |
|
- تهيهكنندگان |
|
- و ... |
اين فهرست همينطور ادامه دارد. اما يك نام از اين فهرست خارج شده است: «رياضيات».
بسياري از فيلمهاي امروزي بدون هندسهي رديابي پرتوها يا اشياي دورانكنندهي «چهارگان» در فضا ممكن نيست. بنابراين دفعهي بعدي كه بر روي صندلي سينما براي لذت بردن از صحنههاي گرافيكي رفتيد پف فيلهايتان را بهسمت «رياضيات» به هوا بريزيد؛ «رياضياتي» كه ستارهي فيلم است!
[1] Whitted's Groundbreaking Paper, "An Improved Illumination Model for Shaded Display", in Communications of the ACM, Volume 23, Issue 6.
[2] منظور از «راديوسيتي» (Radiosity) يك «الگوريتم نور دادن سرتاسري» (Global Illumination Algorithm) است كه براي «آمادهسازي» (رندر كردن) گرافيك سهبعدي كامپيوتري بهكار ميرود. «راديوسيتي» يك نرمافزار «روش المان محدود» (Finite Element Method) است كه براي حل معادلهي «آمادهسازي (رندر كردن)» (Rendering Equation) براي صحنههايي كاملاً «گسترده» (Diffused) است.
بدون شباهت به الگوريتمهاي «مونت كارلو» (Monte Carlo) نظير: «رديابي مسير» (Path Tracing) – كه همه نوع مسيرهاي نوري را دربرميگيرد – بهخصوص روشهاي «راديوسيتي» (Radiosity)، مسيرهايي بهشكل «لگاريتم در پايهي e» را شامل ميشود.
بهعنوان مثال:
ميتوان از مسيرهايي نام برد كه يك منبع نوري را ترك كرده و چند بار (ممكن است «صفر دفعه») قبل از برخورد به چشم بهطور گسترده منعكس ميشود.
روشهاي «راديوسيتي» (Radiosity) اولين بار حدود سال 1329 (1950 ميلادي) در حوزهي مهندسي «انتقال حرارت» (Heat Transfer) توسعه يافت. بعدها در سال 1363 (1984 ميلادي) بهطور ويژه براي كاربرد مسألهي «آمادهسازي» (رندر كردن) تصاوير گرافيكي كامپيوتري بهوسيلهي محققان دانشگاه «كورنل» (Cornell) اصلاح شد. |