|
مطلبي كه با عنوان زنگ تفريح تقديم ميشود توسط اين محقق جوان آماده شده است. |
|
|
 |
|
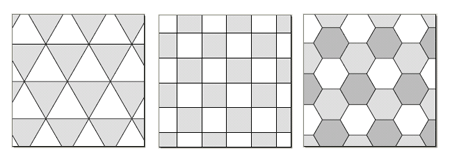
شكل 2 - سه طرح كاشيكاري منظم. |
همهي ما با روشهاي سادهي كاشيكاري صفحه با مثلثهاي متساويالاضلاع، مربعها يا ششضلعيها آشنا هستيم. اينها سه روش قاعدهمند براي كاشيكاري هستند و هريك از آنها از تكرار يكسان يك «چندضلعي منتظم» تشكيل شدهاند.
چندضلعي منتظم» شكلي است كه همهي اضلاعش طول يكسان دارند و زاويههاي بين آنها و كاشيهاي مجاور كاملاً در مرزهايشان مشتركاند. يعني هرگز قسمتي از مرز يك كاشي با بخشي از مرز كاشي ديگر همپوشاني ندارد.
|

|
|
شكل 3 – سه «پنجضلعي» (Pentagon) كه حول يك نقطه
كنار هم قرار بگيرند يك جاي خالي
بهجاي ميگذارند و چهار «پنجضلعي» (Pentagon)
با يكديگر همپوشاني ميكنند. |
در اين مجموعه از كاشيكاريها با چندضلعيهاي منتظم بهوضوح عدد 5 ديده نميشود. بهراستي چرا در يك كاشيكاري منظم، با «پنجضلعي» (Pentagon) مواجه نميشويم؟ به اين نتيجه ميرسيم كه چنين كاشيكارياي وجود ندارد و البته دليل آن هم چندان پيچيده نيست:
يك «پنجضلعي منتظم» (Regular Pentagon) پنج زاويهي داخلي 108 درجهاي دارد. اگر ما تلاش كنيم پنجضلعيها را حول يك نقطه بچينيم خواهيم ديد كه وقتي سه تا از آنها را كنار هم قرار ميدهيم يك «جاي خالي» برجاي ميماند زيرا 324=108×3 كه كمتر از 360 درجه مربوط به يك دايرهي كامل است و هنگاميكه 4 تا از اين «پنجضلعيها» (Pentagons) را كنار هم ميچينيم با يكديگر همپوشاني دارند زيرا 432=108×3 كه از 360 درجهي مربوط به يك دايرهي كامل بيشتر است (شكل 3).
بياييد سعي كنيم اين معما را حل كنيم و تلاش نماييم فارغ از برخي محدوديتها، كاشيكاريهاي جالب ديگري شامل عدد پنج براي صفحه بيابيم. بياييد اين قيد را كه همهي كاشيها تكرار يكسان يك چندضلعي باشند كنار بگذاريم.
اكنون قيد مسأله فقط اين است كه هر كاشي منفرد يك «تقارن پنجگانه» (Five- Fold Symmetry) داشته باشد يعني هر كاشي يك مركز چرخش p داشته باشد بهطوري كه چرخشها حول p بهاندازهي يكپنجم، دوپنجم، سهپنجم و چهارپنجم يك دايره باشد. بهعبارت ديگر چرخش بهاندازهي ضرايب 72 درجه حول p طرح كاشيكاري را تغيير ندهد.
آيا اكنون يافتن مجموعهاي از شكلها با «تقارن پنجگانه» (Five- Fold Symmetry) - كه در كنار هم بتوانند يك صفحه را بپوشانند - ممكن است؟
با فرض در دسترس بودن تعداد زيادي شكل با «تقارن پنجگانه» (Five- Fold Symmetry)، كاشيكاري صفحه بهكمك اين شكلها ممكن بهنظر ميرسد. اگرچه مسأله ظاهراً ساده جلوه ميكند ولي بهطور شگفتاوري دقيق و ظريف است تا جاييكه ذهن برخي از بزرگترين متفكران تاريخ رياضي را سالها به خود مشغول كرده بود. با اين وجود تاكنون جواب كاملي به اين معما داده نشده است.
|
|
|
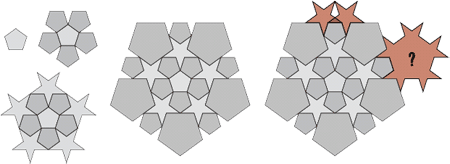
شكل 4 - قطعه قطعه تا ساخت يك طرح. |
بياييد هرگونه استدلال دقيق رياضي در مورد وجود يا عدم وجود اين نوع كاشيكاري را كنار بگذاريم و قدم به قدم تلاش كنيم آن را بسازيم. در شكل 4 با يك «پنج ضلعي منتظم» (Regular Pentagon) شروع ميكنيم: يك شكل خيلي ساده شامل «تقارن پنجگانه» (Five- Fold Symmetry).
ميدانيم به هر ضلع يك «پنج ضلعي منتظم» (Regular Pentagon) ميتوانيم يك «پنجضلعي» (Pentagon) ديگر بچسبانيم. البته با اينكار، پنج شكاف 36 درجهاي در بين آنها بهوجود ميآيد. ميتوانيم اين شكافها را بهكمك ستارههاي «پنجپَر» (Pentacle) بپوشانيم. شكافهايي كه در ميان اين ستاره ايجاد ميشود را ميتوانيم با پنجضلعيهايي (Pentagons) با طول دو برابر پُر كنيم.
اما از اينجا به بعد، راه سادهاي براي اضافه كردن لايهي ديگري به شكلها نداريم. ستارههاي «پنجپَر» (Pentacle) - كه در شكل با رنگ قرمز در گوشهي سمت راست بالا نمايش داده شده - با يكديگر همپوشاني خواهند داشت.
بهعنوان يك راهحل ميتوانيم از شكل ديگري كمك بگيريم. مثلاً: شكلي كه با علامت سؤال نشان داده شده است. ولي معلوم نيست اين شكل جديد بهاندازهي ستارههاي «پنجپَر» (Pentacle) بيضرر باشند. بهعلاوه هيچ دليلي نداريم كه نشان دهد اين شكل جديد به ما اجازه خواهد داد بقيهي صفحه را كاشيكاري كنيم.
|

|
|
شكل 5 - حتي با شروع از يك ستارهي «پنجپَر» (Pentacle)
باز هم به مشكل برميخوريم. |
اين شكل احتمالاً تنها گيرافتادن دوبارهي ما را به تعويق مياندازد. اگر برگرديم و شكل خود را دوباره ولي اينبار با مركز قرار دادن ستارهي «پنجپَر» (Pentacle) - همانطور كه در شكل 5 نشان داده شده - بازسازي كنيم ميتوانيم الگوي بزرگي از كاشيكاري شامل «دهضلعي منتظم» (Regular Decagon) بسازيم. اما نه ... اينبار هم بهدام افتاديم ...
|
|
|
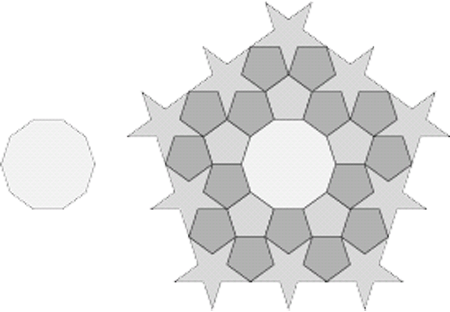
شكل 6 – با يك دهضلعي مركزي نيز نتيجهي لازم را
بهدست نخواهيم آورد. |
شكل 6 نشان ميدهد الگويي با مركز بودن «دهضلعي منتظم» (Regular Decagon) نيز از براوردن خواستهي ما ناتوان است. اگر كمي سمج باشيم ميتوانيم نشان دهيم چهار شكلي كه تاكنون استفاده كردهايم يعني «پنجضلعي» (Pentagon) كوچك، «پنجضلعي» (Pentagon) بزرگ، ستارهي «پنجپَر» (Pentacle) و «دهضلعي» «دهضلعي منتظم» (Decagon) به هيچترتيبي نميتوانند صفحه را كاشي كنند.
|
|
|
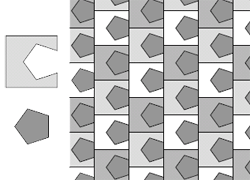
شكل 7 - يك «پنجضلعي» (Pentagon)
از يك مربع بيرون بكشيد. حالا شما
يك طرح كاشيكاري
با «پنجضلعي» (Pentagon) داريد.
بههمين سادگي!! |
|
«لوزي» (Rhombus) شكلي بدون پنج ضلع ولي مناسب! |
اكنون به دو روش ميتوانيم كار خود را ادامه دهيم:
- يك راه اين است كه خانوادهاي از اشكال مختلف طراحي كنيم و بعد ببينيم كار كاشيكاري را تا كجا ميتوانيم ادامه دهيم.
- روش ديگر اين است كه شرط داشتن «تقارن پنجگانه» (Five- Fold Symmetry) را از روي شكلها برداشته از شكلهايي استفاده كنيم كه لزوماً اين تقارن را نداشته باشند.
بهكمك روش دوم ميتوانيم كاشيكاريهايي طراحي كنيم كه بهسادگي تمام صفحه را ميپوشانند. البته بايد راهي بيابيم كه كاشيكاريهايمان مشكلي نداشته باشد. در اين روش، مجاز شمردن استفاده از شكلهاي ديگر، كار را خيلي ساده ميكند.
از هر چندضلعياي كه براي كاشيكاري بهكار رود ميتوان يك «پنجضلعي» (Pentagon) جدا كرد و اين شكل جديد در كنار «پنجضلعي» (Pentagon) جدا شده، سطح صفحه را كاشي خواهند كرد (شكل 7).
|
|
|
شكل 8 - شكلي مانند
«هشتضلعي» (Octagon)
كه با يك «لوزي» (Rhombus) و
دو «پنجضلعي منتظم» (Regular Pentagon)
ساخته شده است. |
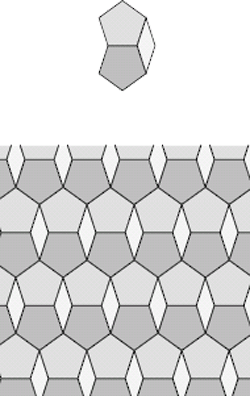
ما رويكرد اصوليتري را پيش خواهيم گرفت. بهسادگي ميتوان ديد دو «پنجضلعي منتظم» (Regular Pentagon) و يك «لوزي» (Rhombus) سي و شش درجهاي، محدودهاي بهشكل «هشتضلعي» (Octagon) تشكيل ميدهند كه ميتواند تمام صفحه را كاشيكاري كند:
بهسادگي ميتوانيد با شروع از يك كاشي و انتقال آن در جهتهاي مختلف، عمودي، افقي و مورب، تمام صفحه را با اين كاشيها بپوشانيد (شكل 8).
در واقع روشهاي متعددي براي كاشيكاري صفحه بهوسيلهي اين شكل وجود دارد. شايد مشهورترين روش كاشيكاري صفحه بهكمك اين شكل، «چينش شعاعي» (Radial Arrangemnet) باشد (شكل 9). اين چينش را هنرمند و رياضيدان آلماني «آلبرت دورر» (Albrecht Dürer) در قرن شانزده ميلادي طراحي كرده است. با افزودن تنها يك «دهضلعي» (Decagon) در مركز اين چينش ميتوانيم طرحي مارپيچ و زيبا ايجاد كنيم (شكل 9).
حدس ميزنيم خوانندگان ما آنقدر باهوش هستند كه با ديدن الگوي كاشيكاري، شيوهي ادامه دادن كاشيكاري را تا جاييكه تمام صفحه پوشيده شود تجسم كنند.
|
پيكربنديهاي اعجابانگيز به روش «جانشينسازي» (Substitution) |
آيا ميتوانيم شكلهايمان را به شكلهاي كوچكتر مناسبي تقسيم كنيم (همانطور كه پيش از اين از «لوزي» (Rhombus) استفاده كرديم)؟
اين پرسش ما را به قانون «جانشينسازي» (Substitution) در نظريهي «كاشيكاري» و شناخت يكي از نوابغ اين رشته يعني «يوهان كپلر» (Johannes Kepler) هدايت ميكند.
وقتي قطعهاي از يك كاشيكاري را داريم بهكمك قانون «جانشينسازي» (Substitution) بهجاي اين قطعه، مجموعهاي از كاشيهاي كوچكتر را مينشانيم (شكل 11).
|
|
|
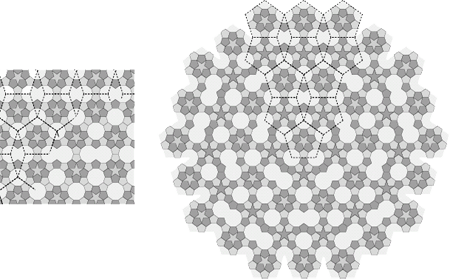
شكل 13 - با بهكارگيري قانون «جانشينسازي» (Substitution) شكل 11
بر روي كاشيكاريهاي شكل 8 و شكل 9 چنين نتيجهاي بهدست ميآيد. |
در شكل 13 نتيجهي كاشيكاري دورهاي با «الگوي شعاعي» (Radial Tilings) نمايش داده شده است. وقتي در قطعهي اصلي هيچ دو «لوزي» (Rhombus) مجاوري وجود نداشته باشند كاشيكاري جديدي با شكلهاي «پنجضلعي» (Pentagon)، ستارهي «پنجپَر» (Pentacle)، «دهضلعي» (Decagon) و شكلي خواهيم داشت كه از بههم پيوستن دو «دهضلعي» (Decagon) بهدست ميآيد.
اعمال قانون «جانشينسازي» (Substitution) در «چينش شعاعي» (Radial Arrangement) «آلبرت دورر» (Albrecht Dürer) به كاشيكاري فوقالعادهاي منجر ميشود. اين موضوع در مقالهاي بهاسم «هارمونيس ماندي» (Harmonice Mundi) نوشتهي «يوهان كپلر» (Johannes Kepler) دربارهي ستارهشناسي و هندسه در قرن هفدهم مطرح شد.
از «يوهان كپلر» (Johannes Kepler) چندين طرح براي «شكلهاي پنجگانه» (Five- Fold Shapes) بهجاي مانده است. احتمالاً اين طرحها در تلاش براي پاسخگويي به مسألهي «كاشيكاري پنجگانه» (Five- Fold Tiling) طراحي شدهاند. قطعهاي كه در شكل 14 ميبينيد بزرگترين طرح اوست. او اين طرح را Aa ناميده است. اين طرح با «دهضلعيهايي» (Decagons) آميخته شده است كه وي آنها را «اعجابانگيز» (Monstre) ناميد.
متني كه ضميممهي اين طرح است نشان ميدهد او چه روشي براي ادامهي ساختار اين طرح در نظر داشته است. در قرن بيستم ميلادي، چند رياضيدان بهطور اصولي نشان دادند كه اين طرح چگونه بايد ادامه يابد. با دقت در طرحهاي ارائه شده توسط «آلبرت دورر» (Albrecht Dürer) و «يوهان كپلر» (Johannes Kepler) به ارتباط نزديك ذهني اين دو انديشمند بزرگ بهرغم حدود دويست سال فاصلهي زماني بيشتر پي ميبريم.
|
|
|
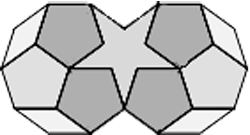
شكل 15 - تقسيم يك شكل نامتداول به
«پنجضلعي» (Pentagon)، ستارهي «پنجپَر»
(Pentacle) و «لوزي» (Rhombus). |
|
تقسيمبندي هميشگي اشكال اعجابانگيز |
قطعاً قانون «جانشينسازي» (Substitution) مشكل «كاشيكاري پنجگانه» (Five- Fold Tiling) را حل نميكند. با اين روش، «لوزي» (Rhombus) از كاشيكاري حذف ميشود ولي بهجاي آن، اشكالي جايگزين ميشوند كه تنها «تقارن دوگانه» (Two-Fold Symmetry) دارند.
وقتي شكلهاي بزرگ را به شكلهاي كوچكتر تقسيم ميكنيم نبايد شكل عجيب ديگري به «پنجضلعي» (Pentagon)، ستارهي «پنجپَر» (Pentacle) و «لوزي» (Rhombus) اضافه كنيم:
|
 |
|
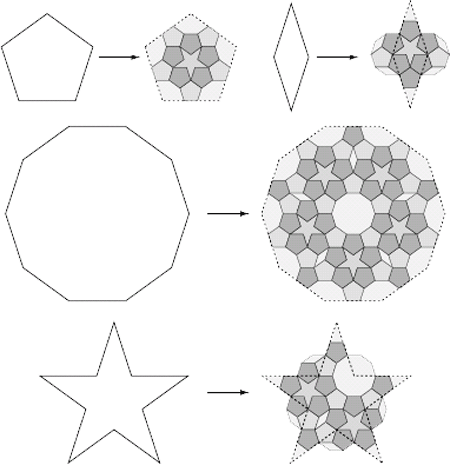
شكل 16 مجموعهي كاملي از اعمال قانون «جانشينسازي» (Substitution)
براي «پنجضلعي» (Pentagon)، ستارهي «پنجپَر» (Pentacle)،
«دهضلعي» (Decagon) و «لوزي» (Rhombus). اگرچه
«جانشينسازي» (Substitution)
دو شكل «لوزي» (Rhombus) و ستارهي «پنجپَر» (Pentacle)
از آنها بيرون ميزند اما كاملاً درست است. |
از آنجا كه قانون «جانشينسازي» (Substitution) براي «لوزيها» (Rhombi) به شكلي نامتداول ميانجامد ميتوانيم زيرتقسيمهاي «لوزي» (Rhombus) و آن شكل نامتداول را با هم تركيب كنيم (شكل 16). اكنون اين قانون را ميتوانيم در مورد زيرتقسيمهاي ستارهي «پنجپَر» (Pentacle) و «دهضلعي» (Decagon) بهكار ببريم.
|
 |
|
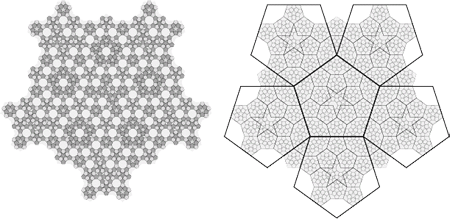
شكل 17 - بخش كوچكي از كاشيكاري كه توسط «لوزي» (Rhombus)
و «پنجضلعي» (Pentagon) با بهكارگيري قانون «جانشينسازي» (Substitution)
در شكل 16 انجام شده است. شكل سمت راست
رابطهي بين كاشيها در تمام سطوح «جانشينسازي» (Substitution)
را نمايش ميدهد. براي مشاهدهي نسخهي بزرگتر عكس
اينجا را كليك فرماييد. |
اما اين زيرتقسيمها به ما اجازه ميدهند نوع ديگري كاشيكاري طراحي كنيم:
|
|
|
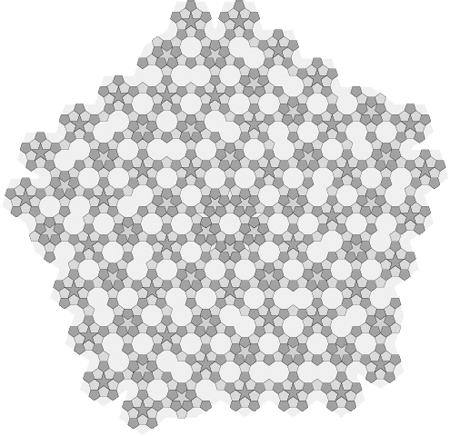
شكل 18 - «چينش مارپيچ» (Spiral Arrangement) شكل 9 كه در آن
«لوزي» (Rhombus) مشابه آنچه در شكل 11 نشان داده شده است
و ساير شكلها مشابه شكل 16 به زيرتقسيمهاي خود
تفكيك شدهاند. ميتوانيم شكلهاي نامتداول را مانند شكل 15
با زيرتقسيمهايشان جايگزين كنيم. |
در واقع در اينجا، ديگر شكل جديدي معرفي نميكنيم و تنها با ايجاد دنبالهاي نامتناهي از زيرتقسيمها، كاشيكاري را با «جانشينسازي» (Substitution) ادامه ميدهيم.
توجه كنيد كه هر طرح جديد شامل «لوزي» (Rhombus) است. بدون انجام عمل زيرتقسيم بهتعداد كافي نميتوانيم به مسألهي كاشيكاري پنجگانه پاسخ دهيم. شكل 18 اعمال قانون «جانشينسازي» (Substitution) را در «چينش مارپيچ» (Spiral Arrangement) شكل 9 نشان ميدهد.
|
كاشيكاري «پِنْرُز» (Penrose) |
سيستم ديگري براي «جانشينسازي» (Substitution) برمبناي «پنجضلعيهاي منتظم» (Regular Pentagon) در قرن بيستم توسط «سر راجر پنرز» (Sir Roger Penrose) ابداع شد و به يك كشف شگفتانگيز انجاميد.
«سر راجر پنرز» (Sir Roger Penrose) مشاهده كرد كه در يك «پنجضلعي» (Pentagon)، آرايشي از شش «پنجضلعي» (Pentagon) كوچك ديگر (مانند تصوير اول در شكل 4) را ميتوان جاي داد. البته اين «جانشينسازي» (Substitution) تمام سطح «پنجضلعي» (Pentagon) اصلي را نميپوشاند بلكه مقداري جاي خالي هم برجا ميماند. اين جاهاي خالي پنج مثلث «متساويالساقين» (Isosceles) با زاويهي رأس 36 درجه هستند.
|
|
|
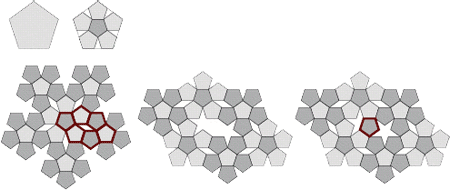
شكل 20 - نخستين گامها براي ايجاد سيستم
«جانشينسازي» (Substitution) «پِنْرُز» (Penrose). |
همانطور كه در شكل 20 ديده ميشود تقسيم ششتايي (تقسيم يك «پنجضلعي» (Pentagon) به شش «پنجضلعي» (Pentagon) كوچك) يك كاشي «لوزي» (Rhombus) شكل را در ميان 6 «پنجضلعي» (Pentagon) محاصره ميكند. در الگويي ديگر، «لوزيها» (Rhombi) در قالب «شكلهايي ميخمانند» (Spiky Shapes) قرار ميگيرند.
|

|
|
شكل 21 - «سر راجر پنرز»
(Sir Roger Penrose). |
«سر راجر پنرز» (Sir Roger Penrose) فهميد «لوزيهاي ميخيشكل» (Spiky Rhombi) ميتوانند با جاسازي «پنجضلعيها» (Pentagon) يعني با تقسيم هريك به «پنجضلعي» (Pentagon)، ستارهي «پنجپَر» (Pentacle) و يك ستارهي «پنجپَر» (Pentacle) نصفه يا يك «قايق كاغذي»!! (Paper Boat) ساده شوند.
|
 |
|
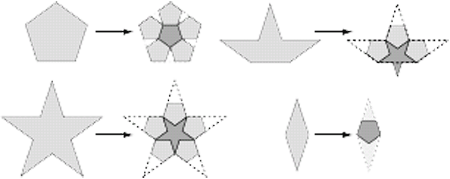
شكل 22 – اعمال قانون «جانشينسازي» (Substitution)
براي چند شكل خاص. |
قرار دادن اين «پنجضلعيهاي» (Pentagon) جديد، قانونهاي «جانشينسازي» (Substitution) مفيدي براي ستارههاي «پنجپَر» (Pentacle) و نيز ستارههاي «پنجپَر» (Pentacle) نصفه پيشنهاد ميكند. در نهايت به خانوادهاي از چهار شكل ميرسيم كه بههمراه قانون «جانشينسازي» (Substitution) طرحها را براي كاشيكاري تمام صفحه گسترش ميدهند (شكل 22).
|

|
|
شكل 23 - قطعهاي از كاشيكاري كه بهكمك
قانون «جانشينسازي پنرز» (Penrose's Substitution Rule) ايجاد شده است. |
در شكل 23 نمونهاي از كاشيكاري بهكمك قانونهاي «جانشينسازي» (Substitution) آمده است.
|

|
|
شكل 24 - «سر راجر پنرز»
(Sir Roger Penrose). |
كشف جديدي كه پيشتر از آن نام برديم با اندكي تغيير در اين سيستم كاشيكاري توليد ميشود. با اعمال تغييرهاي ساده در شش شكل مذكور، «سر راجر پنرز» (Sir Roger Penrose) موفق به طراحي يك «كاشيكاري غيرتناوبي» (Aperiodic Tilings) شد.
|
 |
|
شكل 25 - نوعي «كاشيكاري غيرتناوبي» (Aperiodic Tilings)
كه تنها از دو شكل پايه ساخته شده است. |
برخلاف طرحهايي كه تاكنون ديدهايم اين كاشيكاريها با حركت در امتداد هيچ خط مستقيمي در هيچ جهتي تكرار نميشوند. سالها اين اعتقاد وجود داشت كه هيچ «كاشيكاري غيرتناوبي» (Aperiodic Tilings) - كه از تعدادي شكل محدود تشكيل شده باشد - وجود ندارد. بعدها خود «سر راجر پنرز» (Sir Roger Penrose) بهكمك تنها دو شكل، طرحي شگفتانگيز براي «كاشيكاري غيرتناوبي» (Aperiodic Tilings) خلق كرد (شكل 25).
از نقطهنظر مسألهي «كاشيكاري پنجگانه» (Five- Fold Tiling)، سيستم «پنرز» (Penrose) از آنجايي كه بر دو شكل بنا نهاده شده است بهنظر ميرسد رضايت كمتري را در حل اولين مسألهاي كه ذكر شد [شامل: «لوزي» (Rhombus) و ستارههاي «پنجپَر» (Pentacle)] فراهم كند زيرا باعث ميشود با يك شكل «لوزي» (Rhombus) داراي نقص مواجه شويم.
|
بهدست آوردن شكلهاي عجيب |
آيا كاشيكاريهايي كه تا اينجا ديدهايم در حل مسألهي «كاشيكاري پنجگانه» (Five- Fold Tiling) به ما كمكي ميكند؟! حتماً تا اينجا متوجه شدهايد بهآساني نميتوانيم «لوزيها» (Rhombi) را از طرحهايمان حذف كنيم. حتي ممكن است بتوانيم اين موضوع را ثابت كنيم كه با حذف «لوزي» (Rhombus) در شكلهاي باقيمانده نميتوان تمام صفحه را كاشي كرد.
بهنظر ميرسد «لوزيها» (Rhombi) «نقايصي» (Defects) ايجاد كرده اجازه نميدهند اين «اشكال پنجگانه» (Five- Fold Shapes) عجيب و غريب بدون جاي خالي در كنار هم قرار بگيرند.
اگر دقت كرده باشيد «لوزيها» (Rhombi) باعث ميشوند كه «شكلهاي پنجگانه» (Five- Fold Shapes) بهخوبي در كنار يكديگر بنشينند. اما در عين حال ممكن است راهي براي خنثي كردن يا احتمالاً جايگزين نمودن آنها با اشكال مختلف ديگر وجود داشته باشد تا «تقارن پنجگانه» (Five- Fold Symmetry) حفظ شود.
يك راه براي حذف نواقص كاشيكاري ميتواند «محدود كردن آنها به نواحي بسته» يا «چيدن بسيار نامتراكم» آنها بين كاشيهاي «پنجگانه» باشد. چنين ساختاري ميتواند به فرايندي محدودكننده تبديل شود:
اگر «نواقص» (Defects) را به نواحي كوچك و كوچكتري محدود كنيم يا هرچه بيشتر بهصورت نامتراكم دراوريم در نهايت ميتوانيم به ساختارهايي با نواقص «صفر» برسيم.
در اين زمينه قضيهاي بهنام «قضيهي بسط» (Extension Theorem) وجود دارد كه برطبق آن اگر بتوانيم هر ناحيهاي با هر اندازهاي را بهكمك تعداد متناهي شكل، كاشي كنيم ميتوانيم تمام صفحه را بهكمك آنها كاشيكاري نماييم.
همينطور كه «نواقص» (Defects) نامتراكمتر ميشوند ميتوانيم نواحي بزرگتري را با شكلهاي «پنجگانه» (Five- Fold) كاشي كنيم. سپس با بهكارگيري «قضيهي بسط» (Extension Theorem) ميتوانيم استدلال كنيم كه شكلهاي «پنجگانه» (Five- Fold) براي كاشيكردن تمام صفحه كفايت ميكنند.
اما بههر حال هنوز مشكل حل نشده است زيرا يافتن راهي براي هرچه نامتراكمتر كردن «نواقص» (Defects) مانند همهي روشهاي ديگري كه تاكنون براي حل اين مسأله بهكار بردهايم كاري سخت و پيچيده است.
|
فرو بردن «نواقص» (Defects)!! |
نظرتان راجع به افزودن شكلها چيست؟! يك راهحل طبيعي براي اين مسأله، تركيب «نواقص» (Defects) با كاشيهاي همسايه بهوسيلهي فرو بردن آنها در كاشيهاي جديد با «تقارن پنجگانه» (Five- Fold Symmetry) است.
|
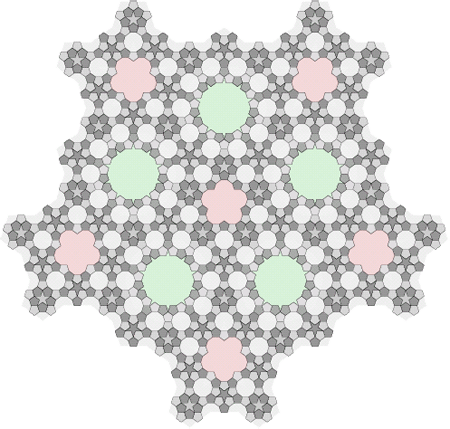
|
|
شكل 26 – فرو بردن كاشيهاي شكل 17. |
در مورد اولين سيستم «جانشينسازي» (Substitution) ميتوانيم بهدنبال كوچكترين مجموعه از كاشيهاي موجود در همسايگي هر «لوزي» (Rhombus) بگرديم كه بتواند با اين روش با آن تركيب شود.
ميتوان بهيقين رسيد كه ميتوانيم بيشتر «لوزيها» (Rhombi) را با ايجاد دو كاشي بزرگتر از شكلهاي بزرگتر متناظر با «دهضلعي» (Decagon) و ستارهي «پنج پر» (Pentacle) حذف كنيم.
شكل 26 نتيجهي تبديلهاي اعمال شده روي قطعهاي از شكل 17 را نمايش ميدهد.
اگرچه همهي «نواقص» (Defects) برطرف ميشوند اما مشكل همچنان باقي ميماند. چون بهزودي به اين نتيجه ميرسيم كه از اين قطعهي جديد نميتوان بدون اينكه «نواقص» (Defects) جديدي بهوجود بيايد صفحه را كاشيكاري كرد. براي فرو بردن اين «نواقص» (Defects) به دنبالهاي نامتناهي از شكلهاي جديد نياز داريم كه بهطور افزاينده بزرگ و بزرگتر ميشوند.
بهلحاظ نظري احتمالاً در اين دنباله بهجايي خواهيم رسيد كه كاشيهاي بزرگ بهوجود آمده ميتوانند با انواع كوچكتري از آنها پُر شوند اگرچه اين احتمال در دوردست محقق خواهد شد.
|
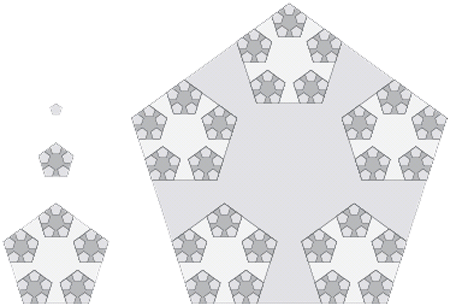 |
|
شكل 27 - يك طرح بسيار ساده از كاشيكاري صفحه
با كاشيهاي پنجگانه؛ در اين طرح از لحاظ «اندازهي كاشيها»
محدوديتي نداريم. هر مرحله ناحيهاي «پنجضلعي» (Pentagon)
ايجاد كرده است. پنج تا از اين كاشيهاي پنجگانه
با اندازهاي سهبرابر بزرگتر در گوشههاي
يك «پنجضلعي» (Pentagon) قرار گرفتهاند.
نتيجه عبارت است از كاشيكارياي با
«پنجضلعيهاي» (Pentagon) كوچك و «چرخهايي» (Wheels)
كه از لحاظ هندسي داراي اندازهاي با افزايش دايمي هستند. |
با اين وجود، اين هم يك روش براي حل اين مسأله تلقي ميشود؛ اينكه بهطور نامحدود فرو بردن «نواقص» (Defects) را ادامه دهيم تا در نهايت كاشيكارياي بهدست آوريم كه هر كاشي آن داراي «تقارن پنجگانه» (Five- Fold Symmetry) باشد.
در واقع اگر مايل باشيم اجازه دهيم كه كاشيهايمان بهطور نامحدودي بزرگ شوند بهسرعت به پاسخهاي سادهتري دست خواهيم يافت (شكل 27).
بهعنوان مثال:
همانگونه كه در شكل 27 نمايش داده شده است اين كاشيكاري نهتنها با كنار هم قرار دادن كاشيها بهصورت پهلو به پهلو بهدست آمده بلكه با فرو بردن آنها در يكديگر با چسباندن پنج «پنجضلعي» (Pentagon) در گوشههاي يك «پنجضلعي» (Pentagon) با اندازهاي سهبرابر بزرگتر انجام شده است.
با تكرار نامتناهي اين فرايند به يك طرح كاشيكاري براي پوشاندن تمام صفحه ميرسيم كه البته «تقارن پنجگانه» (Five- Fold Symmetry) هم دارد.
ولي در هر دو مورد اين خواسته كه كاشيها بهطور دلخواه بزرگ باشند ناكام ميماند.
براي اطمينان از اينكه كاشيها در دامنهاي محدود قرار گيرند رياضيدانان شرايط محدودكنندهاي به اين مسأله افزودهاند. آنان رسماً خواستند كاشيكاري بهطور هماهنگي «محدود» باشد. بايد اعداد مثبت و حقيقياي نظير r و R وجود داشته باشند بهگونهاي كه هر كاشي شامل «ديسكي» با شعاع r بوده و خودش شامل «ديسكي» بهشعاع R باشد.
اما مسألهي «كاشيكاري پنجگانه» (Five- Fold Tiling) در مورد شكلهاي محدود هنوز بدون پاسخ مانده است.
|

|
|
شكل 28 - با دوازده «پنجضلعي» (Pentagon)
ژميتوان سطح يك كره را كاشيكاري كرد. |
پاسخهاي جالب ديگري نيز براي معماي ما [«كاشيكاري پنجگانه» (Five- Fold Tihing)] وجود دارد. اگر از «صفحهي مسطح اقليدسي» (Flat Euclidean Plane) به سطح يك «كره» (Sphere) برويم ميبينيم كه 3 «پنجضلعي كروي» (Spherical Pentagon) ميتوانند پيرامون يك نقطه قرار بگيرند بدون آنكه جاي خالياي بين آنها وجود داشته باشد و در حقيقت ميتوانيم سطح يك كره را بهكمك 12 «پنجضلعي» (Pentagon) كاشيكنيم. اين كاشيكاري مانند يك «دوازدهوجهي متورم» (شبيه بالن) (Dodecahedron) بهنظر ميرسد.
در هندسهي هذلولوي - كه نوع ديگري از «هندسهي غيرمسطح» (Non- Flat Geometry) است - بينهايت روش براي كاشيكاري سطح بهكمك «پنجضلعيهاي منتظم» (Regular Pentagons) وجود دارد.
در واقع بهنظر ميرسد اين مسطح بودن فضاي اقليدسي است كه مانع كاشيكاري سطح به كمك شكلهاي «پنجگانه» (Five- Fold) ميشود. بهزباني ديگر، «پنجگانگي» (Fiveness) و «مسطح بودن» (Flatness) در طول يكديگر زمانهاي سختي را با هم سپري كردهاند!
معماي كاشيكاري «پنجگانه» (Five- Fold Tiling) مانند اغلب مسألههاي نظريهي كاشيكاري توضيحي ساده و پاسخي پيچيده دارند. اين در حالي است كه جواب مثبت به چنين معمايي احتمالاً بايد بهاصطلاح آسان و سر راست باشد اما كشف آن، نياز به كار عميق همراه با خلاقيت دارد.
اثبات اينكه چنين كاشيكاري اي وجود ندارد كاري دشوارتر است. پاسخ منفي تحتتأثير عبارتي دربارهي «همهي كاشيكارهاي ممكن» است كه كاملاً شامل اشكال «پنجگانه» (Five- Fold) باشند. نشان دادن اينكه به چه استدلالهايي از اين دست نياز داريم مشكل است.
پس شما را با مسألهاي اذيتكننده در رياضي مواجه كرديم كه طراحيهاي هندسي جالبي را شامل ميشود و البته سؤالهاي مرتبط بسياري براي مطالعه در اين زمينه وجود دارد.
محققاني نظير: «برانكو گرونبائوم» (Branko Grünbaum)، «جفري كولين شپهارد» (Geoffrey Colin Shephard) و «لودويگ دنزر» (Ludwig Danzer) اولين افرادي بودند كه مسألهي «كاشيكاريهاي پنجگانه» (Five- Fold Tiling) را با «فرو بردن» (Gluing) اشكال «پنجگانه» (Fiive- Fold Shapes) در يكديگر مطرح كردهاند و البته ما ميتوانيم مسألهي «كاشيكاري nگانه» را براي !n>6 پيشنهاد كنيم.
همهي اين مسائل بدون حل باقي ماندهاند. سؤالي كه ميتوان مطرح كرد آن است كه آيا حل مسألهي كاشيكاري «117گانه» سادهتر است يا «كاشيكاري پنجگانه» يا اينكه بههمان اثبات اصلي نياز دارد؟ جواب هرچه باشد ما بهدنبال مشاهدهي اختلاط زيباي طرح رياضيات و هندسه هستيم كه در اين تحقيقها به آن دست مييابيم.