n×nيك مربع لاتين عبارت است از يك ماتريس  با درایه‌های ۱٬۲,۳,...,n به طوری که در هر سطر و ستون درایه‌ها تکراری نباشند. مربع لاتین با مربع‌های وفقی نیز ارتباط دارند ٍ یکی از کاربرد‌های مربه‌های لاتین در مبحث رمزنگاری است.

قضیه: اگر L یک مستطیل لاتین p×q با درایه هایی از مجموعه {3,2,1...n} باشد، آنگاه L را می توان به یک مربع لاتین n×n گسترش داد اگر و تنها اگر مقدار (L(i (تعداد تکرار های i در L) برای هر n>i>1 در شرط زیر صدق کند:

L(i) ≥ p + q – n

اثبات: فرض می کنیم که L قابل گسترش به مربع لاتین n× n باشد:

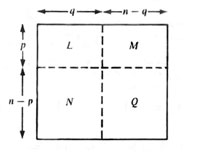
چون i به تعداد (L(i مرتبه در L ظاهر شده و P مرتبه در دو بخش M و L با هم ظاهر می شود.پس (p - L(i در M تکرار شده است. اما از طرفی i به تعداد n - q مرتبه در دو بخش Q و M با هم تکرار می شود. پس داریم:

p - L(i) ≤ n – q → L(i) ≥ p + q – n

برعکس فرض کنیم رابطه L(i) ≥ p + q – n به ازای هر i بر قرار باشد و q<n . روشی ارائه می دهیم که بوسیله آن بتوان L را به مستطیل (p×(q+1 گسترش داد و این روش برای مستطیل بدست آمده در مرحله قبل قابل تکرار باشد و بتواند تا ساختن مستطیل لاتین p×n ادامه پیدا کند. از طرفی بنا بر قضیه ی قبل مطمئن هستیم که این مستطیل p×n قابل گسترش به مربع لاتین n×n است.پس حکم قضیه ثابت می شود.

برای هر p>i>1 مجموعه Ai را به صورت زیر تعریف می کنیم :

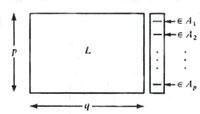
حال نشان می دهیم که خانواده {S={A1 , A2 , A3 ,..., An دارای یک مجموعه نماینده های متمایز شامل مجموعه ی P می باشد. (که این مجموعه را به عنوان ستون اضافی برای گسترش L به مستطیل لاتین (p×(q+1 در نظر می گیریم.)

برای اثبات وجود مجموعه نماینده های متمایز خانواده S باید به دو نکته توجه کنیم.

1)

A1| = |A2| = |A3| = ... = |Ap| = n – q|

2) چون هر i در(p-L(i سطر ظاهر نشده و از طرفی p -L(i) ≤ n – q پس هر i در حد اکثر n-q تا از مجموعه های A1 , A2 , ... , Ap ظاهر شده است. بنا بر این مانند اثبات قضیه قبل اجتماع هر r تا از این مجموعه ها شامل حد اقل r عضو متمایز می باشد.در نتیجه طبق قضیه هال یک مجموعه نماینده های متمایز از خانواده ی مذکور وجود دارد.

حال برای آن که اثبات کنیم مجموعه نماینده های متمایز مورد نظر شامل مجموعه P است، باید نشان دهیم:

| p – (U Ai) | ≤ p - |I|      ,         IC { 1 , 2 , … , p }

و سپس از قضیه کمکی 2 استفاده می کنیم. برای پرهیز از پیچیده شدن مساله این حکم را تنها برای {I={1,2,3,...,r اثبات می کنیم. (در حقیقت ما یک مجموعه r عضوی شامل{A1 , A2 , A3 ,...,Ar} را بررسی می کنیم و بقیه مجموعه ها نیز شبیه همین مورد هستند). بنا بر تعریف داریم :

می دانیم هر عضو p مانند k دقیقاً p+q-n مرتبه در L ظاهر می شود. حال اگر p + q - n < r آنگاه k حد اقل در یکی از Ai ها ظاهر شده. بنا بر این جمع بالا صفر شده و نا مساوی بر قرار می شود.

اما اگر p + q - n ≥ r از لم گفته شده استفاده می کنیم و با در نظر گرفتن m = p + q – n نتیجه می گیریم که :

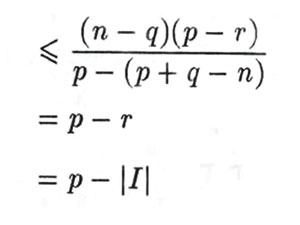
بنا بر نامساوی فوق طبق قضیه هال خانواده S یک مجموعه نماینده های متمایز شامل P دارد.می توانیم این مجموعه نماینده های متمایز را به عنوان ستون اضافی برای گسترش L به مستطیل لاتین (p×(q+1 استفاده کنیم. اگر(L’(i) تعداد مرتبه های حضور عدد i در مستطیل لاتین جدید یعنی ’L باشد، در نتیجه خواهیم داشت: اگر i عضو p نباشد :

اگر i عضو p باشد :

که در هر صورت نتیجه می دهد:

L’(i) ≥ p + q – n + 1

یعنی مستطیل لاتین ’L نیز شرط لازم وکافی برای گسترش دادن را دارد و از این رویه می تواند ادامه پیدا کند تا مستطیل لاتین p×n ساخته شود و از طرفی بنا بر قضیه قبل مطمئن هستیم که این مستطیل می تواند به مربع لاتین n×n گسترش یابد.