زنگتفریح شماره 121
در زنگتفریح شمارهی ۱۱۶ با مربعهای جادویی آشنا شدیم و همچنین با در دست داشتن دو مربع جادویی mدرm و nدرn توانستیم مربعهای جادویی mnدرmn بسازیم. اما از آنجایی که نمیتوانیم مریع جادویی ۲در۲ بسازیم روش فوق کمکی به ساخت مربعهای جادویی که تعداد زوج سطر و ستون دارند نمیکند. البته در همان زنگتفریح ۱۱۶ توانستیم با دوز و کلک یک مربع جادویی ۶در۶ بسازیم. حال در این زنگتفریح میخواهیم با در دست داشتن یک مربع جادویی mدرm که m عددی فرد است، مریعی بسازیم که ۲m سطر و ستون دارد.اگر m=2k+1 باشد، در زنگتفریح ۱۱۶ برای حالت k=1 این کار را انجام دادهایم. حال میخواهیم برای همهی kهای دلخواه این کار را انجام دهیم. این روش به روش LUX کانوی مشهور است.
برای این کار ابتدا یک جدول mدرm میسازیم و خانههای آن را بهشکل زیر پر میکنیم، یعنی k+1 سطر اول را L مینویسیم، سطر بعدی را U و سطرهای آخر را با X پر میکنیم، در نهایت U وسطی را با L بالای آن جابجا میکنیم. در زیر برای k=4 این کار را انجام دادهایم:

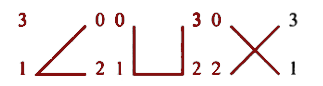
حال هر یک از خانههای جدول فوق را به چهار خانه تقسیم میکنیم و با توجه به الگوی زیر این چهار خانه را با رقمهای ۰، ۱، ۲ و ۳ پر میکنیم. اکنون یک جدول 2mدر2m داریم که آمادهی جادویی شدن است! برای این کار از مربع جادویی mدرmای که از ابتدا در دست داشتهایم استفاده میکنیم. کافیست رقمهای ۰، ۱، ۲ و ۳ هر یک از خانههای بالا را در عدد متناظرش در مربع جادویی ضرب کنیم. مربع جادویی شما آماده است! (البته در این مربع عددها از صفر شروع شدهاند، اگر اصرار دارید که اولین عدد شما ۱ باشد همهی عددها را با ۱ جمع کنید).