زنگتفریح شماره 133
کافی نیست که ذهن قوی داشته باشیم،
مسئله اساسی این است که از آن به خوبی استفاده کنیم.
(رنه دکارت)
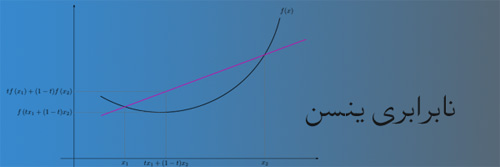
مقدمه
اغلب، مسالههای مختلفی را از ماکزیمم و مینیمم، دربارهی مجموعها، حاصلضرب تابعهای مثلثاتی و برای زاویههای مثلث، در مجلات ریاضی (که در آشنا کردن مردم با ریاضیات نقش اساسی دارند) مطرح میشوند. نابرابری یِنسن، نمونهی خوبی از یگانگی ریاضیات است و نشان میدهد که «چگونه میتوان بسیاری از مسایل مختلف را با یک روش کلی حل کرد».
ینسن
جان ینسن (J. L. W. V. Jensen) (1925-1854)، که بحث ما در این مقاله، بر گِرد نام او دور میزند، مهندس و عضو هیاتمدیره تلفن دانمارک بود. ینسن (که عضو فرهنگستان علوم نیز بود)، قهرمان مطالعه و پژوهش در مورد تابعهای محدب است.
نابرابریهای مثلثاتی زیر را داریم که براساس نتایج ساده از توابع مثلثاتی بهدست میآیند:
(*) α و β دو زاویه با شرط 0≤α≤180° و 0≤β≤180° هستند. داریم:
(1) 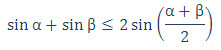
تساوی زمانی است که: α=β است.
(**) میدانیم: α1,α2,…,αn زاویههای مثلثی هستند با شرط 0≤αj ≤180° که j = 1, 2, …, n است. داریم:
(2) 
برابر تنها زمانی برقرار است که α1=α2=...=αn .
اثبات آسان است و به خواننده واگذار میشود.
نتیجههای مشابهی برای سایر تابعهای مثلثاتی مانند کسینوس و ... برقرار است اما نیازی به بحث نیست. نابرابری ینسن این مساله را حل خواهد کرد.
فرض کنید تابع (f(x، برای هر دو مقدار α و β از دامنهی تعریف تابع، با این نابربر ناسازگار باشد:
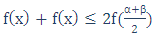
(دامنهی تعریف تابع بازهای از محور اعداد حقیقی است). در ضمن فرض کنید تساوی تنها برای β=α برقرار باشد. در این صورت برای مجموعهی اعداد حقیقی α1,α2,…,αn از دامنهی تعریف تابع داریم:
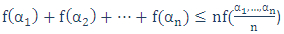
که تساوی تنها برای حالت برابر هم αi ها رخ میدهد. علاوه بر این میتوان نتیجهی مشابهی را، برای حالتی که نابرابریهای (1) و (2) در جهت عکس باشند، بهدست آورد.
اثباتها آسان هستند برای پرهیز از طولانی شدن از ارایه آنها صرف نظر شده است.
تابع f را محدب میگوییم، هرگاه برای هردو مقدار x و y از دامنهی تعریف تابع داشته باشیم:
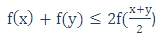
با توجه به این تعریف، نتیجهی (*) را نابرابری ینسن دربارهی توابع محدب میگویند. اکنون بهآسانی میتوان نتیجههای مربوط به حاصلضرب تابعها را تنظیم کرد:
فرض کنید تابع (f(x برای هر دو مقدار α و β از دامنهی تعریف تابع، با این نابرابری سازگار باشد:
(3) 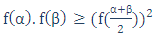
و تساوی تنها برای α=β برقرار باشد. همچنین دامنهی تعریف تابع را، بازهای از عددهای مثبت روی محور اعداد حقیقی فرض کنید. در این صورت خواهیم داشت:
(4) 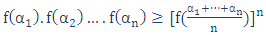
که تساوی تنها برای α1 = α2 = …= αn برقرار است.
مشابه این نتیجه را، برای حالتی که جهت نابرابرها در (3) و (4) عوض شوند، میتوان بهدست آورد.
همانطور که اشاره شد، هدف از نگارش این مقاله این است که دانشآموزان با روش سودمند و کلی برای حل بسیاری از مسالههای ماکزیمم و مینیمم دست پیدا کنند و آن را در زندگی روزمره نیز بهکار گیرند.
غلامرضا پورقلی
دانشجوی دکتری ریاضی
دانشگاه تهران