زنگتفریح شماره 138

در حقیقت تخم توپولوژی از تجزیه و تحلیل کلاسیک معمای هفت پل، توسط لئوناردو اویلر (ریاضیدان سوئیسی)، در سال 1736 بارور گشت. معما به این صورت بود که هفت پل بر روی رودخانهی شهر کنیگسبرگ بسته شده است، چگونه میتوانیم از روی همهی پلها عبور کنیم و به نقطه آغاز حرکت برسیم، بدون اینکه پلی را بیش از یک بار طی کنیم. اویلر نشان داد که معمای هفت پل از نظر ریاضی همانند این است که که بخواهیم شبکهی بستهای را با مسیری متوالی بپیماییم، بدون اینکه از جایی دو بار عبور کنیم. طرح گرافها و پایهی توپولوژی نیز در همین جا ریخته شد.
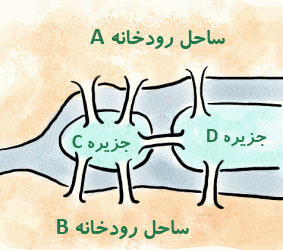
از این گونه معماها که در آن پیمودن مسیری مورد نظر است، در کتاب معما و سرگرمی، زیاد به چشم میخورد. چون همهی این معماها با قضیه گراف و قانون اویلری ارتباط پیدا میکند، پیش از این که به طرح معمایی دیگر بپردازیم، یادآوری چند اصطلاح و قانون را لازم میدانیم.
شبکهی بستهای از خطهای متقاطع را گراف مینامند (شکل 1 یک گراف را نشان میدهد). پارهخطها را یال و انتهای یالها را گره گویند. اگر تعداد یالهایی که به هر گره منتهی میشوند، زوج باشند آن را گره زوج، و در غیر این صورت گره را فرد مینامند. در یک گراف باید به تعداد گرههای زوج و یا فرد توجه کرد. ثابت میشود، تعداد گرههای فرد همیشه زوج است.
حال اگر همهی گرههای یک گراف زوج باشند، میتوانیم شبکه را با یک مسیر متوالی بپیماییم بهطوری که همهی یالها را یک بار و تنها یک بار پیموده و دوباره به هر نقطه دلخواهی که آغاز به حرکت کرده بودیم، برگشت کنیم. اگر گراف دارای دو گره فرد باشد، در صورتی که از یکی از گرههای فرد آغاز به حرکت کنیم، میتوانیم همهی مسیرها را (تنها یک بار) بهطور متوالی بپیماییم، ولی دیگر نمیتوانیم پایان مسیر را به نقطهی آغاز حرکت برسانیم، ناچار مسیر حرکت در گرهی فرد دوم به پایان میرسد.
حال اگر در گرافی بیش از دو گره فرد وجود داشته باشد، پیمایش همهی یالهای آن و تنها یک بار، شدنی نیست، چون روشن است که این گرههای فرد باید یکی از دو سر خط مسیر باشند و میدانیم که هر خط مسیر متوالی، یا دارای دو سر راست است و یا هیچ.
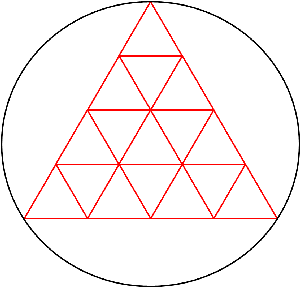
شکل 1: معمای پیمودن شبکه
با بهخاطر سپردن این قانونهای اویلری، معماهایی از این دست بهسادگی حل میشوند. در این گونه معماها ممکن است مسئلهی دیگری نیز مطرح شود که در هر حال با رعایت دستورات اویلر به نتیجه میرسیم. مثلا شبکهی شکل 1 یکی از این گونه معماهاست.
میخواهیم این شبکه را با یک مسیر متوالی ولی با کمترین پیچ و خم بپیماییم. در این جا دیده میشود که تمام گرههای آن زوج هستند. بنابراین امکان پیمودن یک مسیر متوالی در آن هست. با وجود این اجازه داریم، هر چند یک بار که نیاز شدید باشد، مسیری را چه موافق و چه مخالف جهت پیشین، تکرار کنیم و یا از نقطهای برگردیم که در این صورت نقطه برگشت هم یک پیچ و خم بهحساب میآید.
حل معما ساده است ولی دقت میخواهد، در هر صورت اگر به راهحلی که بهدست میآورید مشکوک بودید، به حل زیر توجه کنید.
روی قاعدهی مثلث بزرگ، از دومین گرهی سمت چپ، حرکت را آغاز کنید و به سمت بالا و متمایل به راست تا آن جا که ممکن است پیش بروید، سپس به چپ، بعد پایین و متمایل به راست تا قاعدهی مثلث حرکت کنید. بالا و راست، چپ تا جایی که راه باز است، پایین و راست، راست تا انتهای قاعدهی مثلث بزرگ، بالا تا راس مثلث، پایین تا گوشهی چپ مثلث، دور تا دور دایره را، راست تا گرهی سوم روی قاعدهی مثلث، بالا و چپ تا جایی که میتوانید، راست تا جایی که میتوانید، و سرانجام پایین و چپ تا قاعدهی مثلث. به این ترتیب در یک مسیر متوالی با 13 پیچ و خم که کمترین پیچ و خم ممکن است، شبکه را طی کردهاید.
معماهای مکانیکی، بهویژه آنهایی که با حلقه و نخ سر و کار دارند، رابطهی نزدیکی با نظریه گرهها در توپولوژی دارند. ما در این جا یکی از بهترین آنها را در شکل 2 نمایش دادهایم برای نمونه انتخاب کردهایم. این معما با یک تکه مقوای کلفت یا تخته و مقداری نخ و حلقهای بزرگتر از سوراخ میانی مقوا باشد، ساخته میشود. هر چه تخته یا مقوا بزرگتر و نخ کلفتتر باشد، ساختن آن راحتتر است. معما از ما میخواهد که حلقه روی نخ را از خمیدگی A به خمیدگی B منتقل کنیم، بدون اینکه نخ را پاره کنیم و یا گرهای را باز کنیم.
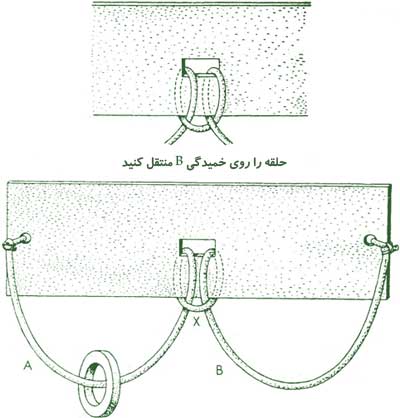
شکل 2
این معما در بسیاری از کتابهای قدیمی معما، شرح داده شده است، که معمولا در بیشتر آنها بهصورت نامطلوبی طرح شده است. به جای اینکه دو سر نخ مانند شکل 2 به تخته گره خورده باشد، هر سر نخ از سوراخی عبور کرده و به مهرهای بسته شده تا از در رفتن نخ جلوگیری شود. چنین طرحی راهحل سادهای دارد که زیبایی چندانی هم در آن بهچشم نمیخورد. کافی است که خمیدگی X را از سوراخهای دو طرف تخته گذرانده و از روی مهرهها عبور دهیم و سپس آنها را بیرون کشیم. این عمل دو خمیدگی A و B را از درگیری با خمیدگی X آزاد میکند. با کشیدن A یا B و یا هر دو، خمیدگی X از سوراخ میانی بیرون میآید، حال حلقه را به سمت راست میرانیم و سپس عکسالعملهای پیشین را انجام میدهیم.

ولی اگر دو سر نخ مانند شکل 2 به دو سر گره خورده باشند، راهحل مذکور به روی ما بسته میشود. ولی به هر صورت این معما دارای راهحل زیبایی است که دو سر نخ، هیچ نقشی را در آن بازی نمیکنند. نکته جالب در این معما این است که اگر نخ طوری بسته شود که مانند تصویر بالا شکل 2، خمیدگی X از زیر و روی نخهای A و B عبور داده شود، راهحلی برای معما پیدا نخواهد شد.
خمیدگی X را با کشیدن به طرف خود، آنقدر شل کنید تا بتوانید حلقه را از میان آن به طرف بالا بکشید. حلقه را روی تخته نگه دارید و خمیدگیهای A و Bرا در جایی که از سوراخ میانه تخته بیرون آمدهاند، با هم بگیرید و آنها را به طرف خود بکشید. این کار دو خمیدگی را از سوراخ میانه بیرون میکشد، حلقه را از میان این دو خمیدگی عبور دهید، دست خود را به پشت تخته ببرید و نخهای پشت سوراخ میانی را از پشت بیرون بکشید تا دو خمیدگی به جای اولش برگردد و خمیدگی X دوباره پیدا شود. حلقه را از میان خمیدگی X به پایین بلغزانید. آن چه را میخواستید بهدست آوردهاید.
غلامرضا پورقلی
دانشجوی دکتری ریاضی
دانشگاه تهران