زنگتفریح شماره ۱۵۷
برنده شدن هميشه به اين معني نيست كه اولين باشي،
بلكه بدين معني است كه بهتر از قبل عمل كرده باشي!
بوني بلير
|
مساله این است که:
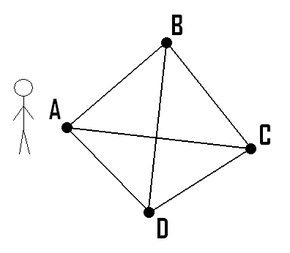
اگر فروشنده دورهگرد از نقطه A شروع به حرکت کند و فواصل بین نقاط مشخص باشد، کوتاهترین مسیر که از تمام نقاط یکبار عبور کند و مجددا به A باز گردد کدام است؟
|
مقدمه
مسئله فروشنده دورهگرد (Travelling salesman problem)، مسئلهای معروف است که ابتدا مسائل مربوط به آن توسط ویلیام همیلتون و توماس کرکمن در سده ۱۸ مطرح شد و سپس در دهه ۱۹۳۰ شکل عمومی آن به وسیله ریاضیدانانی مثل کارل منگر از دانشگاه هاروارد و هاسلر ویتنی از دانشگاه پرینستون مورد توجه قرار گرفت.
و اما شرح مساله:
تعدادی شهر وجود دارد و هزینه رفتن مستقیم از یکی به دیگری را میدانیم. مطلوب است انتخاب کمهزینهترین مسیر که از یک شهر شروع شود و از همه ی شهرها دقیقاٌ یکبار عبور کند و مجدد به شهر شروع بازگردد.
تعداد کل راهحلها برابر است با ½(n-1)! برای ، n>2 که n تعداد شهرها است. در واقع این عدد برابر است با تعداد دورهای همیلتونی در یک گراف کامل با n رأس.
William Rowan Hamilton
مسأله فروشنده دوره گرد یا Traveling Salesman Problem، یکی از مسائل بسیار مهم و کاربردی در علوم کامپیوتر و تحقیق در عملیات است. سه روش کلی برای کد کردن راه حل های مسأله TSP ارائه شده است که در الگوریتمهای مختلفی قابل استفاده هستند. راهحل های سهگاه عبارتند از:
الف) نمایش جواب بهصورت رشته گسسته جایگشتی که در الگوریتمهای زیر قابل استفاده است: الگوریتمهای ژنتیک، شبیه سازی تبرید، جستجوی ممنوعه، جستجوی همسایگی متغیر، بهینهسازی کلونی مورچگان، جستجوی هارمونی و سایر الگوریتمهای بهینهسازی گسسته
ب) نمایش جواب بهصورت کلیدهای تصادفی که در الگوریتمهای زیر قابل استفاده است: الگوریتمهای ژنتیک، بهینه سازی ازدحام ذرات، الگوریتم رقابت استعماری، تکامل تفاضلی، بهینهسازی مبتنی بر جغرافیای زیستی، استراتژیهای تکاملی، برنامهریزی تکاملی و سایر الگوریتمهای بهینه سازی پیوسته
پ) نمایش جواب بهشکل ماتریسهای شبیه فرومون که توسط تمامی الگوریتم های اشاره شده در مورد (ب) قابل استفاده می باشد.
مسئله معادل در نظریه گراف به اینصورت است که یک گراف وزندار کامل داریم که میخواهیم کموزنترین دور همیلتونی را پیدا کنیم.
مسئله تنگراه فروشنده دورهگرد (Bottleneck traveling salesman problem): مسئلهای بسیار کاربردی است که در یک گراف وزندار کموزنترین دور همیلتونی را میخواهد که شامل سنگینترین یال باشد (تعاریف را میتوان از منابع استاندارد مطالعه کرد).
تعمیمیافته مسئله فروشنده دورهگرد دارای ایالتهایی است که هر کدام حداقل یک شهر دارند و فروشنده باید در هر ایالت دقیقاٌ از یک شهر عبور کند. این مسئله به « مسئله سیاستمدار مسافر» نیز شهرت دارد
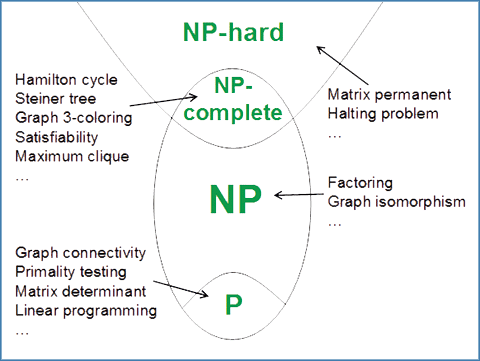
مسئله فروشنده دورهگرد جزء مسائل انپی سخت (NP-hard problem) است (مسایلی که حل دقیق ندارند).
راههای معمول مقابله با چنین مسائلی عبارتند از:
طراحی الگوریتمهایی برای پیدا کردن جوابهای دقیق که استفاده از آنها فقط برای مسائل با اندازه کوچک صورت میگیرد.
استفاده از الگوریتمهای مکاشفهای که جوابهایی بهدست میدهد که احتمالاٌ درست هستند.
پیدا کردن زیرمسئلههایی از مسئله یعنی تقسیم مسئله به مسئلههای کوچکتر تا بشود از الگوریتمهای مکاشفهای بهتر و دقیقتری ارائه کرد.