نخستین بار ریاضیدانی به نام یوهانس مولر معروف به رگیومونتانوس در سال ۱۴۷۱ میلادی مساله‌‌ای را مطرح کرد، که در این‌جا آورده‌ایم. راه‌حلی که در این‌جا می‌آید منسوب به لورش (A. Lorsch) است.

تصور کنید مجسمه‌ای به ارتفاع h فوت روی پایه‌ای به ارتفاع p فوت قرار دارد. شخصی که تراز چشمانش e فوت بالاتر از سطح زمین است، در حالی که به مجسمه چشم دوخته است قدم زنان به آن نزدیک می‌شود. شخص در چه فاصله‌ای از پایه‌ی مجسمه توقف کند تا مجسمه را تا بیشترین حد ممکن بزرگ ببیند؟! یعنی خطوط دید شخص به بالاترین و پایین‌ترین نقطه‌ی مجسمه بزرگترین زاویه را با هم بسازند.

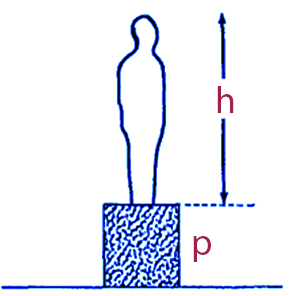
شکل ۱

این مساله فقط زمانی جالب است که تراز چشمان ناظر پایین‌تر از بالای پایه یا بالاتر از مجسمه باشد. از حالا به بعد فرض کنیم e < p.

شکل ۲ نموداری از وضعیت مورد نظر ماست. خطی از بالاترین نقطه‌ی مجسمه، C بر زمین عمود کرده‌ایم، پایین مجسمه را با  B، مکان چشمان ناظر را وقتی روی زمین قدم می‌زند با L، موضع دلخواهی از ناظر را با M، و زاویه‌ی BMC را که وقتی M در امتداد L حرکت می‌کند باید ماکسیمم شود با α نشان می‌دهیم. به علاوه، دایره‌ی K را از نقاط B و C  می‌گذرانیم به طوری که بر خط L مماس باشد.

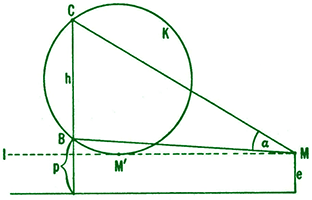
شکل ۲

ادعا: از میان همه‌ی نقاط M روی L، نقطه‌ای که در آن α=∢BMC بزرگ‌ترین مقدار را دارد نقطه‌ی 'M تماس دایره‌ی K با خط L است.

اثبات: برای این‌که نشان دهیم به ازای همه‌ی نقاط 'M≠M روی خط L (در سمت راست مجسمه) داریم BM'C >∢BMC∢ ، از واقعیت‌های زیر استفاده می‌کنیم:

فرض کنید β نشان‌دهنده‌ی زاویه‌ی ‌ BM'C باشد. در این صورت به ازای هر نقطه‌ی P روی قوس BM'C داریم  ∢BPC=β

شکل ۳ را ببینید. که به آسانی ثابت می‌شود که:

الف) اگر R نقطه‌ی دلخواهی در درون دایره باشد، آن‌گاه ∢BPC=β

ب) اگر Q نقطه‌ی دلخواهی در خارج از دایره و در همان طرف وتر BC باشد که قوس بزرگتر قرار دارد، آن‌گاه ∢BPC=β

چون خط L  فقط یک نقطه مشترک با دایره‌ی K دارد که 'M است و چون همه‌ی نقاط دیگر L در سمت راست مجسمه، در خارج K  قرار دارند، از حکم (ب) در بالا نتیجه می‌شود که زاویه‌ی BMC واقعا به ازای M'=M ماکسیمم می‌شود.

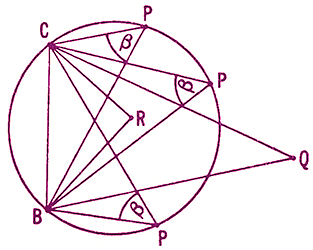
شکل ۳