زنگتفریح شمارهٔ ۱۶۳

مساله چند وزیر یک معمای شطرنجی و ریاضیاتی است که براساس آن باید n وزیر شطرنج در یک صفحه n×n شطرنج طوری قرار بگیرند که هیچکدام زیر ضرب دیگری نباشند. از آنجایی که وزیر بهصورت افقی، عمودی و اُریب حرکت میکند، بنابراین باید هر وزیر را در طول، عرض و قطر متفاوتی قرار دهیم. اولین شکل این مسئله معمای هشت وزیر است. ساده ترین روش برای حل آن به این صورت است که ۸ وزیر را در یک صفحهً معمولی (۸×۸) شطرنج قرار دهیم. این مسئله ۹۲ جواب خواهد داشت که ۱۲ جواب آن متفاوت است و بقیه جوابها از تقارن جوابهای اصلی بهدست میآیند.
نکته جالب این که: مسئله n وزیر در صورتی جواب دارد که n مساوی ۱ یا بیشتر از ۳ باشد. بنابراین مسئله دو وزیر و سه وزیر قابل حل نیستند.
مسئله چند وزیر اولین بار در سال ۱۸۴۸ میلادی توسط Max Bezzel شطرنج باز آلمانی مطرح شد و بعد از آن ریاضیدانان دیگری بر روی این مسئله کار کردند. اولین راه حل توسط Franz Nauck در سال ۱۸۵۰ ارائه شد که به همان مسئله n وزیر تعمیم داده شد. پس از آن Gunther راه حلی به کمک دترمینان بیان کرد که J.W.L. Glaisher آنرا کامل نمود. در سال ۱۹۷۹، Edsger Dijkstra Nauck این مسئله را با استفاده از الگوریتم عقبگرد حل کرد.
هدف از مسئله n وزیر، چیدن n مهره وزیر در یک صفحه شطرنج (n*n) است، به نحوی که هیچ دو مهرهای نباید در یک سطر، ستون یا قطر یکسان باشند. وزیر در خانههای شطرنج به صورت عرضی، طولی و قطری میتواند حرکت کند. مسئله n وزیر از جمله مسائل NP در هوش مصنوعی است که روشهای جستجوی معمولی قادر به حل آنها نخواهد بود.
الگوریتم عقبگرد
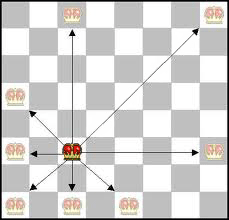
از تکنیک عقبگرد Backtracking برای حل مسائلی استفاده میشود که در آنها دنبالهای از اشیاء از یک مجموعه مشخص انتخاب میشود، به طوری که این دنباله، ملاکی را در بر میگیرد. عقبگرد حالت اصلاح شدهی جست و جوی عمقی یک درخت است. این الگوریتم همانند جست و جوی عمقی است، با این تفاوت که فرزندان یک گره فقط هنگامی ملاقات میشوند که گره امید بخش باشد و در آن گره حلی وجود نداشته باشد. با توجه به اینکه هیچ ۲ وزیری نباید همدیگر را گارد کنند و در یک سطر نمیتوانند باشند، تعداد کل حالتها برای 4n = برابر ۴*۴*۴*۴=۲۵۶ است. در شطرنج یک وزیر میتواند به مهرههایی که در خانههای عمود یا مورب به وی قرار دارند حمله کند. یا به عبارت ریاضی، اگر ردیفها و ستون-های شطرنج را از یک تا هشت شماره گذاری کنیم و وزیر در خانه (i، j) قرار داشته باشد، مهرههایی که در خانههای (i، m) یا (m، j) یا (i ± m، j ± m) قرار دارند توسط وزیر تهدید میشوند.
برای سادگی تشریح این مسئله با استفاده از روش بازگشت به عقب، فرض میکنیم که خانههای شطرنج ۴x۴ و تعداد وزیرها نیز ۴ باشد. سپس بعد از یافتن راه حل برای این مسئله ساده شده، اقدام به نوشتن الگوریتم برای مسئله اصلی میکنیم.
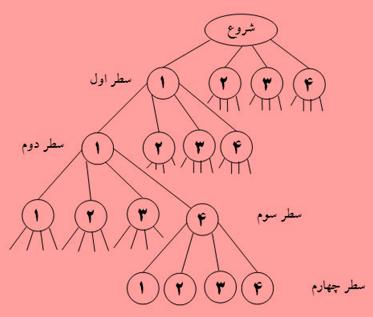
مراحل جستجو برای یافتن جواب را به این صورت دنبال میکنیم که: وزیر اول را در ردیف اول و ستون اول قرار میدهیم.
در ردیف دوم از اولین ستون به جلو رفته و به دنبال خانهای میگردیم که مورد تهدید وزیر اول نباشد و وزیر دوم را در این خانه قرار میدهیم.
همانند قبل، در ردیف سوم از اولین ستون به جلو رفته و به دنبال خانهای میگردیم که مورد تهدید وزیران اول و دوم نباشد. میبینیم که چنین خانهای موجود نیست. پس به عقب یعنی ردیف دوم برگشته و وزیر دوم را به خانهای دیگر از ردیف دوم منتقل میکنیم که مورد تهدید وزیر اول نباشد.
دوباره در ردیف سوم اولین خانهای را مییابیم که مورد تهدید دو وزیر قبلی نباشد. این بار خانه را مییابیم و وزیر سوم را در آن قرار میدهیم.
همانند قبل، در ردیف چهارم به دنبال اولین خانهای میگردیم که مورد تهدید وزیران پیشین نباشد. چنین خانهای موجود نیست. به ردیف قبل یعنی ردیف سوم باز میگردیم تا خانهای دیگر برای وزیر سوم بیابیم. خانه دیگری وجود ندارد. به ردیف قبل یعنی ردیف دوم بر میگردیم تا خانه دیگری برای وزیر دوم پیدا کنیم. به آخرین ستون رسیدهایم و خانه دیگری نیست. به ردیف قبل یعنی ردیف اول بر میگردیم و وزیر اول را یک ستون به جلو میبریم.
در ردیف دوم اولین خانهای را مییابیم که مورد تهدید وزیر اول نباشد و وزیر دوم را در آن خانه قرار میدهیم.
در ردیف سوم اولین خانهای را مییابیم که مورد تهدید وزیران اول و دوم نباشد و وزیر سوم را در آن خانه میگذاریم.
در ردیف چهارم اولین خانهای را مییابیم که مورد تهدید وزیران پیشین نباشد. این بار خانه را مییابیم و وزیر چهارم را در آن خانه قرار میدهیم.
به یک جواب میرسیم. حال اگر فرض کنیم که این خانه جواب نیست و به مسیر خود ادامه دهیم، احتمالا" میتوانیم جوابهای دیگری نیز بیابیم.

الگوریتم مونت کارلو
از الگوریتم مونت کارلو برای برآورد کردن کارایی یک الگوریتم عقب گرد استفاده میشود. الگوریتمهای مونت کارلو، احتمالی هستند، یعنی دستور اجرایی بعدی گاه به طور تصادفی تعیین میشوند. در الگوریتم قطعی چنین چیزی رخ نمیدهد. الگوریتم مونت کارلو مقدار مورد انتظار یک متغیر تصادفی را که روی یک فضای ساده تعریف میشود، با استفاده از مقدار میانگین آن روی نمونه تصادفی از فضای ساده بر آورد میکند. تضمینی وجود ندارد که این برآورد به مقدار مورد انتظار واقعی نزدیک باشد، ولی احتمال نزدیک شدن آن، با افزایش زمان در دسترس برای الگوریتم، افزایش مییابد.

روش مکاشفهای
برای حل این مسئله که دارای ۹۲ جواب است، باید تکنیکهایی جهت کاهش حالات، روش Brute Force یا امتحان تک تک جوابها انجام شود. تعداد همه حالاتی که میتواند در روش Brute Force چک شود برابر 216، 777، 16 یا هشت به توان هشت است! یکی از روشهای حل این مسئله برای n>=4 یا n=1 استفاده از روش مکاشفهای (heuristic method) است:
1- عدد n را بر عدد ۱۲ تقسیم کن و باقی مانده را یادداشت کن.
۲- به ترتیب اعداد زوج ۲ تا n را در لیستی بنویس.
۳- اگر باقی مانده ۳ یا ۹ بود، عدد ۲ را به انتهای لیست انتقال بده.
۴- به لیست اعداد فرد ۱ تا n را به ترتیب اضافه کن، اما اگر باقی مانده ۸ بود اعداد را دو به دو باهم عوض کند (مثلا ۱ و۳ و ۵ و۷ و۹ تبدیل به ۳ و۱ و ۷ و ۵ و۹ میشه)
۵- اگر باقی مانده ۲ بود جای ۱ و۳ را با هم عوض کن و ۵ را به انتهای لیست ببر.
۶- اگر باقی مانده ۳ یا ۹ بود، اعداد ۱ و ۳ را به انتهای لیست ببر.
۷- حال با استفاده از لیست بدست آمده وزیرها در صفحه شطرنج چیده میشوند، بطوریکه جای وزیر ستون اول، اولین عدد لیست، جای وزیر ستون دوم، دومین عدد لیست و...
این الگوریتم یک راه حل برای حل این مسئلهاست، برای بدست آوردن همه حالات از روشهای دیگری میتوان استفاده کرد. روش حل مسئله ۱۲ راه حل یکتا دارد که با در نظرگیری تقارن و چرخش به ۹۲ حالت قابل تبدیل است.
روشهای جستجوی محلی
میتوان به مسئله ۸ وزیر به عنوان یک مسئله بهینهسازی نیز نگاه کرد که در آن هدف بهینه کردن تعداد گاردهای جفت وزیرها میباشد.به عنوان مثال فرض کنید در صفحه شطرنج معمولی، ۸ وزیر را به دو روش زیر قرار دهیم:


در روش چینش سمت چپ، ۳ وزیر و در روش چینش سمت راست، ۴ وزیر همدیگر را گارد میدهند. بنابراین روش چینش قبلی بهینه تر از روش چینش فعلی است. در واقع میتوان مسئله بهینه سازی را به صورت زیر تعریف کرد. فرض کنید S مجموعه همه جوابهای ممکن برای مسئله باشد. در صورتی S* میتواند جواب مسئله باشد که به ازای همه جوابهای موجود در S، S* بهینه تر از دیگر جوابها باشد. در مسئله ۸ وزیر دیدیم که جوابی بهینه است که تعداد گاردهای جفت وزیر آن کمتر باشد.
روشهای جستجوی محلی همگی حالتهای همسایه حالت فعلی را برای رسیدن به بهینهترین جواب بررسی میکنند. از این رو وجود دو تابع در همه این روشهای جستجو الزامی است. اولین تابع میزان بهینگی جواب مسئله ارزیابی میکند و تابع دوم یکی از حالتهای همسایه حالت فعلی را انتخاب میکند.
نحوه اجرا و طراحی الگوریتم برای انتخاب حالت همسایه در این روشهای جستجو از اهمیت ویژهای برخوردار است. به عنوان مثال برای مسئله ۸ وزیر میتوان به شکلهای زیر حالتهای همسایگی را تولید کرد:
۱) دو وزیر به تصادف انتخاب شوند و جای آن دو باهم عوض شود.
۲) یکی از وزیرها به تصادف انتخاب شوند و شماره سطر آن به تصادف تغییر کند.
۳) یک وزیر به تصادف انتخاب شود و یک خانه به سمت بالا یا پایین حرکت کند.