زنگتفریح شمارهٔ ۱۶۶
قرنها پیش انسان میپنداشت که زمین تخت است. پس از آنکه کروی بودن زمین اثبات شد، دانشمندان به فکر افتادند تا محاسبات خود را که تا پیش از آن روی صفحه تخت انجام شده بود، روی کره انجام دهند. برای مثال اگر شما یک خط کش فلزی داشته باشید، هرگز نمیتوانید آن را به طور کامل روی کره قرار دهید؛ زیرا خطکش تخت و کره دارای انحنا است. این امر نشان میدهد که خط راستی که در هندسه اقلیدسی با آن آشنا شدیم، روی کره کاربردی ندارد. این ایده باعث شد تا ریاضیدانان به فکر یک تعریف جدید برای خط راست روی کره بیافتند. این تلاشها سبب شد تا هندسه کروی بوجود بیاید. هندسه کروی در زمانهای دور برای تعیین جهت در خشکی و آب به کار میرفت و امروزه در بسیاری از مسائل از جمله پرتاب و حرکت موشکها و ماهوارهها کاربرد دارد.
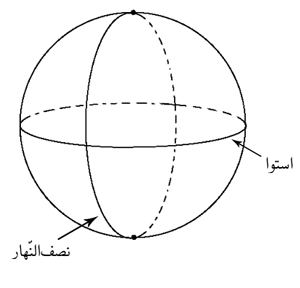 |
از هندسه اقلیدسی سهبعدی میدانیم که از هر سه نقطه در فضا یک صفحه منحصر بفرد میگذرد. اکنون فرض کنید a و b دو نقطه روی کره و O مرکز کره باشد. میخواهیم مفهوم خط راست روی کره بین این دو نقطه را تعریف کنیم. فرض کنید P صفحهای باشد که از سه نقطه a، b و O میگذرد. محل تماس این صفحه با کره دقیقا یک دایره است که شعاعاش با شعاع کره برابرست. این دایره را دایره عظیمه گذرنده از نقاط a و b مینامیم. دایرههای عظیمه و هر کمانی از آنها را ژئودزیک گویند که معادل مفهوم خط راست در صفحه است. در واقع شما قبلا هم دایره عظیمه دیدهاید. خط استوا و نصفالنهارها نمونههایی از دایرههای عظیمه کره زمین هستند.
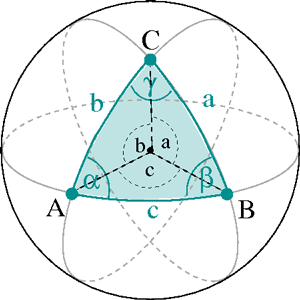
دو نقطه a و b این دایره را به دو کمان تقسیم میکنند. این دایره عظیمه را خط بین نقاط a و b و طول کمان کوچکتر را فاصله بین دو نقطه میگویند. مانند هندسه اقلیدسی، منظور از یک مثلث روی کره، قسمتی از کره است که بین سه دایره عظیمه (خطهای راست کره) محصور شده است. مثلث روی کره با مثلث صفحه تفاوتهای بسیاری دارد. برای مثال مجموع زوایای داخلی مثلث کره میتواند بیش از °۱۸۰ باشد. هدف ما در این مقاله محاسبه مساحت مثلث روی کره به روشی بسیار ساده است. برای انجام شهودی این محاسبه میتوانید از یک پرتقال به عنوان کره و کش مو یا کش پول به جای دایرههای عظیمه استفاده کنید. البته با داشتن یک ماژیک میتوان نقاط و زوایای روی پرتقال را هم مشخص کرد.

|
با ماژیک سه نقطه روی پرتقال مشخص کنید. برای راحتی کار از سر پرتقال (مرکز بالایی آن) به عنوان یکی از نقاط استفاده کنید.
|
 |
|
یک کش را روی پرتقال طوری قرار دهید که از سر پرتقال و یکی دیگر از نقاط بگذرد. این کار پرتقال را به دو نیم تقسیم میکند. سعی کنید این دو نیمه متقارن و با هم برابر باشند. با اینکار میتوانید پرتقال را به عنوان یک کره و سر آن را به عنوان قطب شمال تصور کنید. در این صورت کشی که روی پرتقال گذاشتهاید نقش نصفالنّهار را دارد که از قطب شمال، نقطه مشخص شده با ماژیک و قطب جنوب (تَه پرتقال) میگذرد.
|
 |
|
کش دوم را طوری روی پرتقال قرار دهید که از سر و نقطه سوم روی پرتقال بگذرد و دوباره پرتقال را تا حد امکان به دو نیم متقارن و مساوی تقسیم کند.
|
 |
|
قبل از اینکه کش سوم یا همان ضلع سوم مثلث را اضافه کنیم، به بررسی قسمت محصور شده بین این دو کش میپردازیم. این قسمت را یک قاچ از پرتقال مینامیم. زاویه بالایی بین دو کش را α مینامیم.
|
 |
|
دو کش روی پرتقال یکدیگر را دوباره در قطب جنوب (تَه پرتقال) قطع میکنند و زاویه بین آنها برابر با زاویهشان در قطب شمال خواهد بود. آن را نیز با α نشان میدهیم.
|
 |
|
برای محاسبه مساحت مثلث روی کره به مساحت قاچهای روی کره نیاز خواهیم داشت. به سادگی دیده میشود که مساحت قاچ فقط به زاویه α بستگی دارد و با بزرگتر یا کوچکتر شدن آن تغییر میکند. مساحت کره به شعاع r برابر است با 4πr2. یک قاچ با زاویه π رادیان یا °۱۸۰ یک نیمکره با مساحت 4πr2/2=2πr2 است. برای زاویه π/2، قاچ مورد نظر یکچهارم از کره است که مساحت آن با 4πr2/4=πr2 برابر است. به همین ترتیب برای زاویه دلخواه α، مساحت قاچ آن از نسبت
بدست میآید و برابر است با 2αr2.
|
|
حال به اضافه کردن ضلع سوم مثلث میپردازیم. کش سوم را روی دو نقطهای که قبلا به هم وصل نشدهاند. قرار دهید. دوباره سعی کنید که نیمههای پرتقالی که با کش سوم ایجاد شدهاند تا حد ممکن متقارن و مساوی باشند.
|
 |
|
دو زاویه دیگر را با β و δ نامگذاری میکنیم. دقت کنید که یک مثلث مساوی با این مثلث در طرف دیگر پرتقال به وجود آمده است.
|
 |
اکنون همه اجزایی که برای محاسبه مساحت یک مثلث روی کره لازم داریم آمادهاند. بقیه کار با محاسبه مساحت قاچها انجام میشود. وقتی سه کش روی پرتقال قرار دادیم، ۶ قاچ با زوایای مختلف به وجود آمد. دو قاچ با زاویه α، دو قاچ با زاویه β و دو قاچ با زاویه δ. البته قاچهای دیگری با زوایای π-α، π-β و π-δ نیز روی کره هستند که برای محاسبات ما کاربرد ندارند. هر نقطهای که داخل مثلث δβα قرار دارد، در یک قاچ α، یک قاچ β و یک قاچ δ نیز قرار دارد. همین اتفاق برای نقاط مثلث مساوی با δβα که در طرف دیگر پرتقال قرار دارد نیز میافتد. هر کدام از نقاط روی پرتقال که خارج از این دو مثلث هستند فقط داخل یکی از قاچهای α، β و δ قرار دارند. در نتیجه اگر مساحت این ۶ قاچ را با هم جمع کنیم همه نقاط خارج مثلثها یکبار و هر کدام از نقاط داخل مثلثها ۳بار شمرده(محاسبه) میشوند. یعنی با جمع مساحت ۶ قاچ، مساحت همه نواحی خارج دو مثلث را یکبار و مساحت داخل هر یک از مثلثها را ۳بار حساب کردهایم. بنابراین برای محاسبه مساحت پرتقال از طریق قاچها، مساحت دو مثلث همشکل را دوبار بیشتر از حد نیاز اضافه کردهایم. اکر مساحت مثلث δβα را با T نمایش دهیم آنگاه:
4πr2=2αr2+2βr2+2δr2-4T.
در نتیجه:
T=(α+β+δ-π) r2.