مارپيچ اعداد و اعداد اول
آيا مسابقهي شماره 6 ما را مطالعه كردهايد؟ در اين مسابقه ما اعداد طبيعي را به گونهاي خاص و به صورت يك مارپيچ مرتب كردهايم. شايد در ابتدا اين موضوع به نظرتان مهم نيايد و يا حتي ارزش فكر كردن هم نداشته باشد، ولي پروفسور اولم (Stanislaw M. Ulam (1909–1984 اينگونه نيانديشيد. هنگامي كه او در يك سخنراني خوابآور و كسل كننده بيصبرانه منتظر تمام شدن سخنراني بود، براي سرگرم كردن خود، اعداد را به صورت مارپيج روي يك تكه كاغذ مينوشت، ناگهان او متوجه چيزي شد، او به اعداد اول دقت كرد و متوجه يك نظم مختصر در محل قرارگيري اعداد اول در اين مارپيچ شد. اولم متوجه شد كه اعداد اول علاقه دارند روي خطوط قرار گيرند، البته مثال نقض زياد بود و براحتي ميتوان اعداد اول مهجور و تنهايي را در اين مارپيچ يافت، ولي تعداد اين اولها به اندازهي كافي كم بود كه اولم از خير بررسي يك دنبالهي مارپيچي بزرگ از اعداد طبيعي نگذرد. اگر مارپيچ را براي اعداد زيادي بسازيم و به آن دقت كنيم به يقين حق را به اولم خواهيد داد.

اعداد اول هميشه معماي حلنشدني دنياي رياضيات و نظريهي اعداد بوده و هيچ فرمول جبري براي ساخت آنها كشف نشده است. شايد در اولين نگاه اعداد اول زياد مهم به نظر نيايند : اعدادي كه تنها بر خود و 1 بخشپذيرند. ولي قضيهي بعدي در مورد اعداد اول موضوع را عوض ميكند : هر عدد صحيح به صورت يكتا به حاصلضربي از توانهاي اعداد اول تجزيه ميگردد. با وجود چنين نقش مهمي در نظريهي اعداد، ماهيت اعداد اول هنوز براي رياضيدانان معمايي است كه اميدي به پاسخ به آن وجود ندارد. پس هر نكتهاي كه به شناخت اين موجودات پيچيده كند گامي بزرگ در دنياي اعداد و رياضيات محسوب ميگردد.
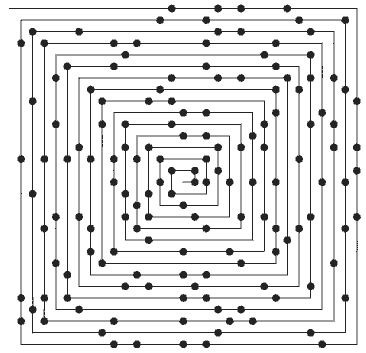
اولم و همكارانش در موسسهي تكنولوژي لوسآلاموس آمريكا براي اطمينان بيشتر با استفاده از كامپيوترهاي آن زمان كه در زمان خود بهترين بودند اين مارپيچ را براي اعداد طبيعي تا 65000 رسم كردند و نتيجه رضايت بخش بود؛ خطهاي مورب، افقي و عمودي از اعداد اول در مارپيچ واضح بودند. اين نتيجه شروعي بود براي تحقيقات بيشتر در اعداد اول با نگاهي نو.

اين خطوط ميتوانند ما را به سمت ساختن بررسي فرمولهاي جبري كه به ساخت اعداد اول منجر ميگردد راهنمايي كند. به عنوان مثال دنبالهي مورب شامل اعداد 5، 19، 41 و 71 مقادير تابع 4x2+10x+5 به ازاي 3 تا 0 = x ميباشند.
همچنين دنبالهي قطري 7، 23، 47 و 79 ، مقادير تابع 4x2+4x-1 به ازاي 4 تا 1 = x است.
براي يافتن نتايج جالبتر مارپيچ را با عددي غير از 1 شروع ميكنيم. بياييد مارپيچمان را با 17 شروع كنيم. در جدول زير اين مارپيچ را تا عدد 137 رسم كردهايم و اعداد اول با رنگ آبي مشخص گرديدهاند.
|
107 |
108 |
109 |
110 |
111 |
112 |
113 |
114 |
115 |
116 |
117 |
|
106 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
81 |
118 |
|
105 |
72 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
82 |
119 |
|
104 |
71 |
46 |
29 |
30 |
31 |
32 |
33 |
54 |
83 |
120 |
|
103 |
70 |
45 |
28 |
19 |
20 |
21 |
34 |
55 |
84 |
121 |
|
102 |
69 |
44 |
27 |
18 |
17 |
22 |
35 |
56 |
85 |
122 |
|
101 |
68 |
43 |
26 |
25 |
24 |
23 |
36 |
57 |
86 |
123 |
|
100 |
67 |
42 |
41 |
40 |
39 |
38 |
37 |
58 |
87 |
124 |
|
99 |
66 |
65 |
64 |
63 |
62 |
61 |
60 |
59 |
88 |
125 |
|
98 |
97 |
96 |
95 |
94 |
93 |
92 |
91 |
90 |
89 |
126 |
|
137 |
136 |
135 |
134 |
133 |
132 |
131 |
130 |
129 |
128 |
127 |
در شكل بالا قطر اصلي، مقادير تابع4x2+2x+17 مي باشند. اين چندجملهاي به احتمال زياد شما را به ياد فرمول معروف اويلر (Euler) كه براي ساخت اعداد اول پيشنهاد داده بود مياندازد : x2+x+17 . شانزده مقدار اوليهي اين تابع همگي اعدادي اولاند. فرمول معروفتر اويلر، x2+4x+41 ميباشد. اگر مارپيچ را با عدد 41 شروع كنيم، قطر اصلي شامل 40 عدد اصلي كنار هم ميباشد.
|
131 |
132 |
133 |
134 |
135 |
136 |
137 |
138 |
139 |
140 |
141 |
|
130 |
97 |
98 |
99 |
100 |
101 |
102 |
103 |
104 |
105 |
142 |
|
129 |
96 |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
106 |
143 |
|
128 |
95 |
70 |
53 |
54 |
55 |
56 |
57 |
78 |
107 |
144 |
|
127 |
94 |
69 |
52 |
43 |
44 |
45 |
58 |
79 |
108 |
145 |
|
126 |
93 |
68 |
51 |
42 |
41 |
46 |
59 |
80 |
109 |
146 |
|
125 |
92 |
67 |
50 |
49 |
48 |
47 |
60 |
81 |
110 |
147 |
|
124 |
91 |
66 |
65 |
64 |
63 |
62 |
61 |
82 |
111 |
148 |
|
123 |
90 |
89 |
88 |
87 |
86 |
85 |
84 |
83 |
112 |
149 |
|
122 |
121 |
120 |
119 |
118 |
117 |
116 |
115 |
114 |
113 |
150 |
|
161 |
160 |
159 |
158 |
157 |
156 |
155 |
154 |
153 |
152 |
151 |
علاوه بر تغيير در عدد آغازين مارپيچ، ميتوان شكل مارپيچ را تغيير داد و باز هم با بررسي اعداد اول نظم مشابهي را در آن مشاهده كرد :
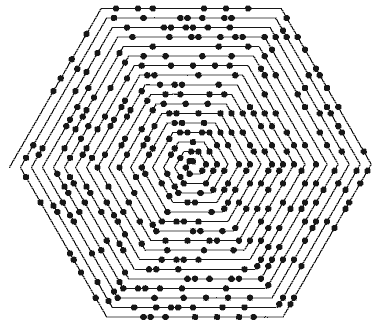

بررسيها كماكان ادامه دارند؛ با تغيير در نوع مارپيچ نتايج جالبي بدست آمده كه نوع چينش اعداد اول به موضوعي جالب براي تحقيق و پژوهش تبديل گشته است .