n مقدمه
حتماً با «مثلث خيام – پاسكال» آشنا هستيد:
حال آيا در مورد «فراكتال»ها (معادل فارسي آن «برخال» است) چيزي شنيدهايد. در اين مورد در كتابهاي درسي رياضياتان مطالبي گفته شده است.
در واقع «برخال»ها موجوداتي هندسياند كه هرچه آن را از نزديك نگاه كنيم شبيه شكل نخستين است مانند: «گل كلم». به اين اشيا اصطلاحاً «خودمتشابه» گويند.

| | 
|
ایدهي «خود متشابه» در اصل توسط «لایبنیتس» بسط داده شد. او حتی بسیاری از جزئیات را حل کرد. در سال ۱۸۷۲ «کارل وایرشتراس» مثالی از تابعی را پیدا کرد با ویژگیهای غیربصری که در همهجا پیوسته بود ولی در هرجا مشتقپذیر نبود. گراف این تابع اکنون «برخال» نامیده میشود.
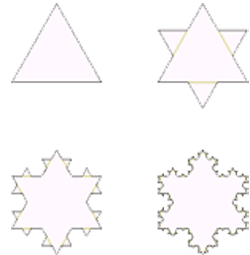
در سال ۱۹۰۴ «هلگه فون کخ» بههمراه خلاصهای از «تعریف تحلیلی وایرشتراس»، تعریف هندسیتری از تابع متشابه ارائه داد که حالا به «برفدانه کخ» معروف است. در سال ۱۹۱۵ «واکلو سرپینسکی» مثلثاش را و سال بعد فرشاش (برخالی) را ساخت.
ایدهي «منحنیهای خودمتشابه» توسط «پاول پیر لوی» مطرح شد او در مقالهاش در سال ۱۹۳۸ با عنوان «سطح یا منحنیهای فضایی» و «سطوحی شامل بخشهای متشابه نسبت به کل» منحنی برخالی جدیدی را توصیف کرد.
منحنی «لوی سي. گئورگ کانتور»مثالی از زیرمجموعههای خط حقیقی با ویژگیهای معمول ارائه داد. این «مجموعههای کانتور» اکنون بهعنوان«برخال» شناخته میشوند.
اواخر قرن نوزدهم و اوایل قرن بیستم «توابع تکرار شونده در سطح پیچیده» توسط «هانری پوانکاره»،«فلیکس کلاین»، «پیر فاتو» و «گاستون جولیا» شناخته شده بودند. با این وجود بدون کمک گرافیک کامپیوتری آنها نسبت به نمایش زیبایی بسیاری از اشیایی که کشف کرده بودند، فاقد معنی بودند.
در سال 1960 «بنوا مندلبرو» تحقیقاتی را در شناخت خودمتشابهای طی مقالهای با عنوان «طول ساحل بریتانیا چقدر است؟ خود متشابهای آماری و بعد کسری» آغاز کرد. این کارها براساس کارهای پیشین «ریچاردسون» استوار بود.
در سال ۱۹۷۵ «مندلبروت» جهت مشخص کردن شيئی که بعد «هاوسدورف بیسکویچ» آن بزرگتر از بعد توپولوژیک است کلمهي «برخال» را ایجاد کرد.
او این تعریف ریاضی را از طریق شبیهسازی خاص کامپیوتری تشریح کرد.
nمثلث خيام - پاسكال
حال با اين توضيح مختصر در مورد برخالها برميگرديم به «مثلث خيام – پاسكال».
در مورد اين مثلث زياد شنيدهايم از جمله در مورد كاربرد فراوانش در نظريهي اعداد و تركيبيات.
حال ميخواهم يك «برخال» ساده را در اين مثلث به شما نشان دهم. موضوعي كه باعث ميشود اين مثلث جايي را نيز در دنياي برخالها – يعني سيستمهاي ديناميكي – پيدا كند.
مسأله خيلي ساده است، تمام اعداد زوج را در «مثلث خيام – پاسكال» پاك كنيد، آنچه باقي ميماند برخالي معروف است با نام «مثلث سرپينسكي»: