پنجشنبه ۶ ارديبهشت ۱۴۰۳   |  كاربر مهمان   |    
 مسابقه‌ی تصادفی

 
 
 بازي با اعداد (مسابقه‌ي شماره‌ي 45)
بازي با اعداد (مسابقه‌ي شماره‌ي 45)مسابقه كامپيوتر
روي تخته تعدادي عدد طبيعي نوشته شده است ... سؤال همراه با جواب

بازي با اعداد





سؤال
روي تخته تعدادي عدد طبيعي نوشته شده است. در هر مرحله، يك عدد روي تخته مانند: 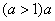 را پاك مي‌كنيم و به‌جاي آن  و  مي‌نويسيم.

اين كار را آن‌قدر ادامه مي‌دهيم تا همه‌ي اعداد روي تخته برابر با 1 شوند.

حال فرض كنيد در ابتدا فقط عدد  روي تخته نوشته شده باشد. تعداد اعداد متفاوتي كه در طول عمليات فوق روي تخته نوشته مي‌شود را بناميد. مثلاً: .


زيرا به‌جاي 7، دو عدد 3 و 4 را مي‌نويسيم. سپس به‌جاي 4، 2 تا 2 و به‌جاي 3، 1 و 2 را مي‌نويسيم.


در پايان نيز به‌جاي هر 2، دو تا 1 مي‌نويسيم. بنابراين 5 عدد مختلف 1، 2، 3، 4 و 7 در طول اين عمليات روي تخته نوشته مي‌شوند.

بزرگ‌ترين مقدار  به‌ازاي  چند است؟

جواب

دو حالت براي عدد  در نظر مي‌گيريم:

الف –  عددي فرد
اگر  عدد «فرد» باشد آن‌گاه دو عدد  و  «زوج» و ديگري «فرد» است.

اگر عدد «فرد» را  و عدد «زوج» را  در نظر بگيريم چون دو عدد  و  متوالي هستند بنابراين در شمردن ، تمام اعداد توليد شده در شمردن  نيز به‌كار رفته‌اند. در اين حالت مي‌توان تشاوي ذيل را نتيجه گرفت:




چون در محاسبه‌ي  دو عدد  و  نسبت به اعداد توليد شده در محاسبه‌ي  بيش‌تر هستند.

ب –  عددي زوج

اگر  عدد «زوج» باشد آن‌گاه دو عدد   و  با هم برابر بوده و آن را  مي‌ناميم. در اين حالت نيز با كمي دقت به‌تساوي ذيل دست مي‌يابيم:





از طرف ديگر معلوم مي‌شود كه اگر عدد  در بازه‌ي  در نظر گرفته شود آن‌گاه عدد  و يا ي تعريف شده در فوق در بازه‌ي  قرار خواهد گرفت؛ به‌اين معنا كه اگر حداكثر مقدار در بازه‌ي  برابر  باشد آن‌گاه حداكثر مقدار در بازه‌ي  برابر  خواهد شد.


حداكثر مقدار در بازه‌ي  برابر 5 است؛ بنابراين حداكثر مقدار در بازه‌‌هاي ذيل به‌ترتيب 7، 9، 11، ...، 21 و 23 خواهد شد:

، ، ، ...، و .


در مورد عدد 3999 مقدار  به‌شكل ذيل برابر 23 مي‌شود:
1386/9/9 لينک مستقيم
فرستنده :
امیرحسین شاپوری HyperLink HyperLink 1386/9/25
مـتـن : من با ++C برنامه را نوشتم و بدست آمد که عدد 1324 اُم اف n که برابر با 8078 عدد مختلف است در محدوده ی 1 تا 4000 بیشترین مقدار است. اگر متن برنامه را میخواهید برایتان میفرستم.
پاسـخ : ايميل فرستنده: amirvoldy@yahoo.com
تاريحخ ارسال: 1386/9/19
اميرحسين جان!
از اين‌كه براي حل اين مسأله با ++C برنامه نوشته‌اي نشان‌دهنده‌ي علاقه‌ي بسيار زيادت به كامپيوتر است.
اما فكر مي‌كنم به سؤال مسابقه با دقت توجه نكرده‌اي. براي راهنمايي مي‌تونم اين توصيه رو بهت بكنم كه منظور اين سؤال اينه كه هر عددي از مجموع دو عدد به‌دست مي‌آيد. اين دو عدد بزرگ‌ترين عددهايي هستند كه جمع اون‌ها مي‌شه عدد مورد نظر.
يعني اين‌كه اگر عدد زوج باشه معلومه كه دو عددي كه جمعشون عدد زوجه، مساوي‌اند و اگر فرد باشه ...
خودت تا آخر جواب سؤال رو ادامه بده!
آفرين بر شما كه از ابزارها (برنامه‌ي ++C) به‌خوبي استفاده مي‌كني.
انشاءالله موفق باشي.
فرستنده :
مسعود دشتی فرد HyperLink HyperLink 1386/9/25
مـتـن : پاسخ مسابقه شماره 45:
17
پاسـخ : ايميل فرستنده: masoud_dcd@yahoo.com
تاريخ ارسال: 1386/9/17
مسعود جان!
خيلي ممنون كه در مسابقه شركت كردي. اما راجع به راه‌حلت توضيح ندادي. منتظر جواب تكميليت هستيم.
انشاءالله موفق باشي!
فرستنده :
مرتضی HyperLink HyperLink 1386/9/25
مـتـن : پاسخ مسابقه شماره 45:
18
پاسـخ : ايميل فرستنده: dayeri63@gmail.com
تاريخ ارسال: 1386/9/17
مرتضي جان!
راجع به روش رسيدن به جوابت توضيح بيش‌تري بده!
منتظر جوابت هستيم.
فرستنده :
arman_o71 HyperLink HyperLink 1386/9/25
مـتـن : برای 3999 = 23

1 2 3 4 7 8 15 16 31 32 62 63 124 125 249 250 499 500 999 1000 1999 2000 3999
پاسـخ : ايميل فرستنده: arman.ordookhani@gmail.com
تاريخ ارسال: 1386/9/11
آرمان جان!
بارك‌الله! جوابت كاملاً صحيح است.
انشاءالله موفق باشي.
فرستنده :
ناشناس HyperLink HyperLink 1386/9/25
مـتـن : عدد3999.در طول عملیات23عددمتفاوت3999و2000و1999و1000و999و500و499و250و249و125و124و63و62و32و31و16و15و8و7و4و3و2و1روی تخته نوشته می شوند
پاسـخ : ايميل فرستنده: s_man_s20@yahoo.com
تاريخ ارسال: 1386/9/10
دوست عزيزم!
جوابت كاملاً صحيح است. اما ازت خواهش مي‌كنم از اين به‌بعد، نام و ايميلت را نيز اعلام كن تا بتوانيم ضمن ارسال هديه‌ي مسابقه، با نامت نيز آشنا شويم.
موفق باشي!
نظر شما پس از تاييد در سايت قرار داده خواهد شد
نام :
پست الکترونيکي :
صفحه شخصي :
نظر:
تایید انصراف
 المپیاد کامپیوتر

 

     

 

  

صفحه‌ي اصلي
     

 

راهنماي سايت
     

 

  

آموزش
     

 

بانك سوال
     

 

  

مسابقه
     

 

  

زنگ تفريح
     

 

  

مصاحبه و گزارش
     

 

  

معرفي كتاب
     

 

  

مشاوره
     

 

  

پرسش‌و‌پاسخ‌علمي
     

 

اخبار

 

فعاليت‌هاي علمي
 بازديدها
خطایی روی داده است.
خطا: بازديدها فعلا" غیر قابل دسترسی می باشد.
 

سرویس‌های رشد:

فهرست:

وزارت آموزش و پرورش > سازمان پژوهش و برنامه‌ريزی آموزشی
شبکه ملی مدارس ایران (رشد)