 واضح است كه وقتي واضح است كه وقتي 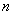 عددي «زوج» باشد راهحلي براي رابطهي عددي «زوج» باشد راهحلي براي رابطهي .gif) وجود ندارد بهخاطر اينكه وجود ندارد بهخاطر اينكه .gif) يا يا .gif) يا «زوج» بوده و بنابراين نسبت به يا «زوج» بوده و بنابراين نسبت به 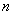 «اول» نيستند. «اول» نيستند.
وقتي 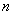 عددي «زوج» باشد هرگز آرايشي از عددي «زوج» باشد هرگز آرايشي از .gif) در مورد كارتها وجود ندارد بهگونهاي كه از هر در مورد كارتها وجود ندارد بهگونهاي كه از هر .gif) از عدد صفر تا از عدد صفر تا .gif) ، تنها عدد ، تنها عدد .gif) (در بين اعداد صفر تا (در بين اعداد صفر تا .gif) ) در رابطهي ) در رابطهي .gif) صدق ميكند. صدق ميكند. شرايطي كه در آن براي هر عدد .gif) ، رابطهي ، رابطهي .gif) تنها با عدد تنها با عدد .gif) برقرار باشد جايگشتهاي برقرار باشد جايگشتهاي .gif) و و .gif) از از .gif) خواهد بود. خواهد بود. اكنون .gif) را بهشكل ذيل تعريف ميكنيم: را بهشكل ذيل تعريف ميكنيم:
(رابطهي 3)
توجه كنيم كه داريم:
(رابطهي 4)
علت آن است كه عبارتهاي داخل «براكتها» جمع اعداد صحيح از صفر تا .gif) هستند. هستند. اما از آنجايي كه لازم است .gif) جايگشتي از اعداد صحيح از صفر تا جايگشتي از اعداد صحيح از صفر تا .gif) باشد بايد باشد بايد .gif) معادل جمع آن اعداد صحيح باشد بهعبارت ديگر: معادل جمع آن اعداد صحيح باشد بهعبارت ديگر:
(رابطهي 5)
از آنجايي كه 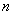 عددي «زوج» است براي بعضي از مقادير عددي «زوج» است براي بعضي از مقادير .gif) داريم: داريم:
(رابطهي 6) از آنجايي كه .gif) داريم: داريم:
(رابطهي 7)
اين با رابطهي 4 - كه در آن .gif) است - در تناقض ميباشد. نتيجه ميگيريم كه تعداد افراد است - در تناقض ميباشد. نتيجه ميگيريم كه تعداد افراد .gif) نميتواند «زوج» باشد. نميتواند «زوج» باشد. |