 راه حل اول
راه حل اول
منظور از اصطلاحهاي شهر «فرد» و «زوج» شهرهايي است تعداد راههاي آسفالتهي خروجي از آن شهرها بهترتيب «فرد» و «زوج» است. براي اين منظور از لمي با عنوان: «لم دوستي» (Handshake) استفاده ميكنيم؛ مطابق اين لم: «مهم نيست چه جادههايي آسفالته هستند مهم آن است كه تعداد شهرهاي زوج، عددي «زوج» (ممكن است «صفر») باشد».
براي بررسي صحت اين لم، فرض كنيد 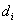 تعداد راههاي آسفالتهي خروجي شهر
تعداد راههاي آسفالتهي خروجي شهر .gif) باشد. مجموع راههاي آسفالتهي خروجي كليهي شهرها يعني:
باشد. مجموع راههاي آسفالتهي خروجي كليهي شهرها يعني: .gif) با دو برابر مجموع تعداد راههاي خروجي كليهي شهرها برابر است.
با دو برابر مجموع تعداد راههاي خروجي كليهي شهرها برابر است.
فرض كنيد تعداد شهرهاي «زوج» عددي «فرد» باشد در اينصورت تعداد شهرهاي «زوج» عددي «فرد» ميشد (چون مجموع آنها عددي «زوج» است). در اين مسأله 500 شهر وجود دارد و 500 نيز عددي «زوج» محسوب ميشود. اما طبق فرض جمع شهرهاي «زوج» بايد عددي «فرد» ميشد و اين يك تناقض است.
با استفاده از «لم دوستي» (Handshake) ميتوانيم الگوريتمي ايجاد كنيم كه سرانجام راهها را بهگونهاي آسفالت كند كه همهي شهرها «فرد» باشند:
 |
 راه حل دوم
راه حل دوم
كشور «كانتري» را يك گراف متصل (شبكهاي از رؤوس كه با يالهايي به هم متصل شدهاند) در نظر ميگيريم كه در آن هر شهر يك «رأس» و هر جادهي خاكي - كه دو شهر را بههم مرتبط ميكند – يك «يال» محسوب ميشود.
تعداد «رؤوس» عبارت است از:
براي هر .gif) هر مسيري از رأس
هر مسيري از رأس .gif) را به رأس
را به رأس .gif) را درنظر ميگيريم (ميدانيم چنين مسيري وجود دارد زيرا گراف متصل است). سپس بر روي هر «يال» علامتي ميگذاريم تا مسير مذكور مشخص شود.
را درنظر ميگيريم (ميدانيم چنين مسيري وجود دارد زيرا گراف متصل است). سپس بر روي هر «يال» علامتي ميگذاريم تا مسير مذكور مشخص شود. همچنين تمام راهها (يالها) را آسفالت ميكنيم تا اينكه تعداد علامتها «زوج» باشد. براي اينكه نشان دهيم اين روش خواستههاي ما را براورده ميكند كافي است ثابت كنيم براي يالهاي وابسته به هر رأس داراي تعداد «زوجي» از كليهي علايم وجود دارد.
بنابراين مجموع تعداد چنين يالهايي با تعداد «فردي» از علايم، عددي «فرد» خواهد بود.
اما همهي رويدادهاي رأس .gif) را در نظر بگيريد؛ يالهاي وابسته به رأس
را در نظر بگيريد؛ يالهاي وابسته به رأس .gif) داراي تعداد «فردي» از علامتها خواهند بود بهخاطر اينكه مجموع تعداد چنين يالهايي با تعداد فردي از علامتها عددي «فرد» خواهد بود.
داراي تعداد «فردي» از علامتها خواهند بود بهخاطر اينكه مجموع تعداد چنين يالهايي با تعداد فردي از علامتها عددي «فرد» خواهد بود.
اما همهي رويدادهاي رأس .gif) در هر يك از 500 مسير را در نظر بگيريد (توجه كنيد كه رأس
در هر يك از 500 مسير را در نظر بگيريد (توجه كنيد كه رأس .gif) پايان يكي از اين مسيرها است). بنابراين يكي از يالهاي وابسته به آن داراي علامت است. هر رويداد ديگر رأس
پايان يكي از اين مسيرها است). بنابراين يكي از يالهاي وابسته به آن داراي علامت است. هر رويداد ديگر رأس .gif) بخش داخلي از يك مسير محسوب ميشود؛ بنابراين داراي دو علامت خواهد بود:
بخش داخلي از يك مسير محسوب ميشود؛ بنابراين داراي دو علامت خواهد بود:
| - يكي در يال ورودي به رأس .gif) |
| - ديگري در يال خروجي از آن. |
اين بدينمعنا است كه كل تعداد علامتهاي وابسته به رأس .gif) عددي «فرد» است. بدينترتيب مسأله ثابت ميشود.
عددي «فرد» است. بدينترتيب مسأله ثابت ميشود.