| موارد كاربردي از گرافهاي ساده و گرافهاي «معادل» و گرافهاي «يكريخت» (Isomorphism) |
موارد ذيل را ميتوان نشان داد: |  اگر گراف اگر گراف  «ساده» (Simple) باشد خواهيم داشت: «ساده» (Simple) باشد خواهيم داشت:
(رابطهي 1) | |  اگر گرافهاي اگر گرافهاي  و و .gif) «يكريخت» (Isomorphism) باشند يعني داشته باشيم: «يكريخت» (Isomorphism) باشند يعني داشته باشيم:
(رابطهي 2) در اين صورت خواهيم داشت:
(رابطهي 3)
(رابطهي 4) ولي عكس اين رابطه برقرار نيست بهعبارت ديگر نميتوان از رابطههاي 3 و 4 رابطهي 2 را بهدست آورد.
| |  دو گراف دو گراف  و و .gif) «سادهي» و «يكريخت» (Isomorphism) هستند اگر و فقط اگر يك تابع «يك به يك» نظير: «سادهي» و «يكريخت» (Isomorphism) هستند اگر و فقط اگر يك تابع «يك به يك» نظير: .gif) وجود داشته باشد بهگونهاي كه وجود داشته باشد بهگونهاي كه .gif) اگر و فقط اگر داشته باشيم: اگر و فقط اگر داشته باشيم:
| |  فرض كنيد فرض كنيد  گرافي «ساده» باشد؛ در اين صورت رابطهي ذيل برقرار است: گرافي «ساده» باشد؛ در اين صورت رابطهي ذيل برقرار است:
(رابطهي 5) اگر و فقط اگر  «كامل» باشد. «كامل» باشد. | |  تعداد يالهاي گراف «دوبخشي كامل» (Complete Bipartite Graph) تعداد يالهاي گراف «دوبخشي كامل» (Complete Bipartite Graph) .gif) از رابطهي ذيل بهدست ميآيد: از رابطهي ذيل بهدست ميآيد:
(رابطهي 6)
| |  اگر اگر  گرافي «ساده» (Simple) و «دوبخشي» (Bipartite) باشد در اين صورت خواهيم داشت: گرافي «ساده» (Simple) و «دوبخشي» (Bipartite) باشد در اين صورت خواهيم داشت:
(رابطهي 7) | |  تعاريف ذيل را بهدقت توجه كنيد: تعاريف ذيل را بهدقت توجه كنيد:
|  يك گراف « يك گراف «.gif) بخشي» (k-Partite) گرافي است كه مجموعه رؤوس آن ميتواند به بخشي» (k-Partite) گرافي است كه مجموعه رؤوس آن ميتواند به .gif) زيرمجموعه بهگونهاي تقسيم شود كه دو انتهاي هيچ يالي در يك زيرمجموعه وجود نداشته باشد. زيرمجموعه بهگونهاي تقسيم شود كه دو انتهاي هيچ يالي در يك زيرمجموعه وجود نداشته باشد.
| |  يك گراف « يك گراف «.gif) بخشي كامل» (Complete k-Partite) گرافي است كه «ساده» بوده و در آن هر رأسي كه رأس ديگر متصل شده است در زيرمجموعهي يكساني نباشد. بخشي كامل» (Complete k-Partite) گرافي است كه «ساده» بوده و در آن هر رأسي كه رأس ديگر متصل شده است در زيرمجموعهي يكساني نباشد. | |  يك گراف « يك گراف «.gif) بخشي كامل» (Complete m-Partite) با بخشي كامل» (Complete m-Partite) با .gif) رأس كه در آن هر بخش داراي رأس كه در آن هر بخش داراي .gif) يا يا .gif) رأس باشد با رأس باشد با .gif) نشان داده ميشود. نشان داده ميشود. |
ميتوان نشان داد رابطهي ذيل دربارهي يك گراف «.gif) بخشي كامل» (Complete k-Partite) همواره برقرار است: بخشي كامل» (Complete k-Partite) همواره برقرار است:
(رابطهي 8) كه در آن داريم:
(رابطهي 9) همچنين ميتوان نشان داد: اگر  يك گراف « يك گراف «.gif) بخشي كامل» (Complete m-Partite) با بخشي كامل» (Complete m-Partite) با .gif) رأس باشد در اين صورت داريم: رأس باشد در اين صورت داريم:
(رابطهي 10)
| | ياداوري – تساوي در رابطهي 10 يعني: .gif) زماني برقرار است كه گرافهاي زماني برقرار است كه گرافهاي  و و .gif) «يكريخت» باشند بهعبارت ديگر داشته باشيم: «يكريخت» باشند بهعبارت ديگر داشته باشيم:
(رابطهي 11)
| |  تعريف ذيل را درنظر بگيريد: تعريف ذيل را درنظر بگيريد:
يك گراف «.gif) مكعب» (k-Cube) گرافي است كه رؤوس آن مكعب» (k-Cube) گرافي است كه رؤوس آن .gif) تايي از «صفر» و «يك» هستند كه دو رأس آن به يكديگر متصل هستند اگر و فقط اگر دو رأسشان دقيقاً در يك مؤلفه با يكديگر تفاوت داشته باشند. تايي از «صفر» و «يك» هستند كه دو رأس آن به يكديگر متصل هستند اگر و فقط اگر دو رأسشان دقيقاً در يك مؤلفه با يكديگر تفاوت داشته باشند. بهعبارت ديگر اگر .gif) عددي طبيعي باشد منظور از « عددي طبيعي باشد منظور از «.gif) مكعب» گرافي است كه رأسهاي آن همهي دنبالههاي مكعب» گرافي است كه رأسهاي آن همهي دنبالههاي .gif) رقمي از «صفر» و «يك» هستند و دو رأس در اين گراف مجاور بوده هرگاه دنبالههاي متناظرشان دقيقاً در يك مؤلفه اختلاف داشته باشند (شكل 1). رقمي از «صفر» و «يك» هستند و دو رأس در اين گراف مجاور بوده هرگاه دنبالههاي متناظرشان دقيقاً در يك مؤلفه اختلاف داشته باشند (شكل 1).
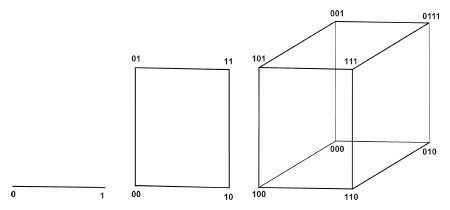
| شكل 1 – گراف «.gif) مكعب» بهترتيب از سمت چپ: مكعب» بهترتيب از سمت چپ:
«يك مكعب»، +«دو مكعب» و «سه مكعب». |
ياداوري - توجه داشته باشيد كه شكل 26 در زنگ تفريح شمارهي 35 تنها يك گراف «3 مكعب» است.
ميتوان نشان داد كه يك گراف «.gif) مكعب» (k-Cube) داراي ويژگيهايي نظير ذيل است: مكعب» (k-Cube) داراي ويژگيهايي نظير ذيل است:
| - تعداد رؤوس = .gif) | | - تعداد يالها = .gif) | | - گرافي «دوبخشي» (Bipartite) است. |
| |  «مكمل» گراف (Complement) «مكمل» گراف (Complement)
«مكمل» (Complement) يك گراف «ساده» – كه معمولاً با .gif) نشان ميدهند - يك گراف «ساده» با مجموعه رؤوس نشان ميدهند - يك گراف «ساده» با مجموعه رؤوس .gif) و دو رأس «مجاور» در و دو رأس «مجاور» در .gif) است اگر و فقط اگر رؤوس در گراف است اگر و فقط اگر رؤوس در گراف  «مجاور» نباشند. «مجاور» نباشند.
| |  گراف «خود مكمل» (Self-Complement) گراف «خود مكمل» (Self-Complement)
يك گراف «ساده» نظير:  «خود مكمل» (Self-Complement) است اگر داشته باشيم: «خود مكمل» (Self-Complement) است اگر داشته باشيم:
(رابطهي 12) ميتوان نشان داد كه اگر گرافي «خود مكمل» (Self-Complement) باشد در اين صورت خواهيم داشت:
(رابطهي 13)
| |  «همريختي» (Automorphism) «همريختي» (Automorphism)
بنابر تعريف «همريختي» (Automorphism) يك گراف عبارت است از: يكريختي آن گراف بر روي خودش (شكل 2).
بهعنوان مثال: قرينههاي آينهاي يك گراف نسبت به محورهاي عمودي و افقي ميتواند بهعنوان «همريختهاي» يك گراف محسوب شوند.
.gif)
| شكل 2 – نمونهاي از گرافهاي
«همريختي» (Automorphism).
| | .gif)
| شكل 3 – گراف «ستاره» (Star)
و گرافهاي «همريخت» آن. |
| | مثالي ديگر: يك گراف «ستاره» (Star) داراي شش گراف «همريخت» است (شكل 3). موارد ذيل را ميتوان دربارهي «همريختي» (Automorphism) اثبات كرد:
|  «همريختي» (Automorphism) «همريختي» (Automorphism)
«همريختي» (Automorphism) يك گراف «سادهي»  ميتواند بهعنوان جايگشتي بر روي ميتواند بهعنوان جايگشتي بر روي .gif) درنظر گرفته شود كه «مجاورت» را حفظ ميكند و اينكه چنين جايگشتهايي، يك گروه درنظر گرفته شود كه «مجاورت» را حفظ ميكند و اينكه چنين جايگشتهايي، يك گروه .gif) (با عنوان: گروه «همريخت» گراف (با عنوان: گروه «همريخت» گراف  ) تحت عمليات غيرمعمول تركيب تشكيل ميدهند. ) تحت عمليات غيرمعمول تركيب تشكيل ميدهند.  براي هر گراف «سادهي» براي هر گراف «سادهي»  رابطهي ذيل برقرار است: رابطهي ذيل برقرار است:
(رابطهي 14) 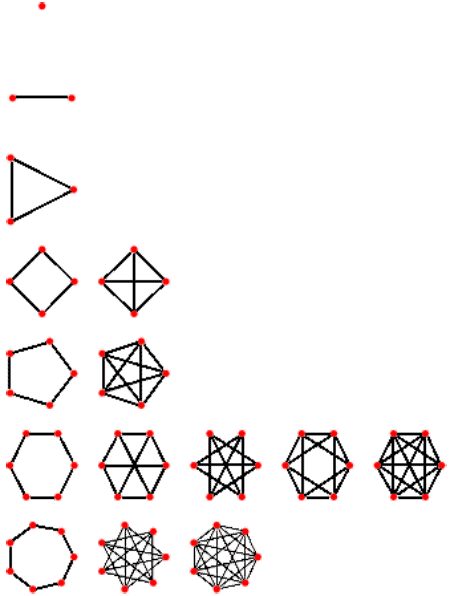
| شكل 4 – نمونههايي از گرافهاي
«رأس متقارن» (Vertex Transitive). | | .gif)
| شكل 5 – سمت چپ و راست بهترتيب
گراف «يگانه»(Singleton) و گراف «دو مسيره» (2-Path Graph). | | 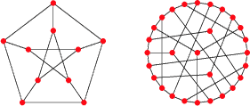
| شكل 6 – سمت چپ و راست بهترتيب
گراف «پيترسون» (Peterson) و گراف «كوگزتر» (Coxeter). | | .gif)
| شكل 7 – سمت چپ و راست بهترتيب گراف «مكعب متقارن»
(Cubic Transitive Graph 66) و گراف «كوگزتر مثلث جايگزين»
(Triangle Replaced Coexeter Graph). |
| |  گراف «رأس متقارن» (Vertex Transitive) گراف «رأس متقارن» (Vertex Transitive)
يك گراف «ساده»، «رأس متقارن» (Vertex Transitive) است اگر براي هر دو رأس .gif) و و .gif) ، يك «عنصر» (Element) نظير: ، يك «عنصر» (Element) نظير: .gif) در در .gif) وجود دارد بهگونهاي كه داشته باشيم: وجود دارد بهگونهاي كه داشته باشيم:
(رابطهي 15) بهعبارت ديگر، يك گراف «رأس متقارن» (Vertex Transitive) است اگر گروه «همريختي» (Automorphism) آن براي رؤؤسش، متقارن عمل كند. به بياني ديگر، شرط لازم و كافي براي آنكه يك گراف «رأس متقارن» (Vertex Transitive) باشد آن است كه با «مكملش» (Complement) همارز باشد.
.gif)
| شكل 8 – نمونههايي از گرافهاي «يال متقارن» (Edge Transitive). | | 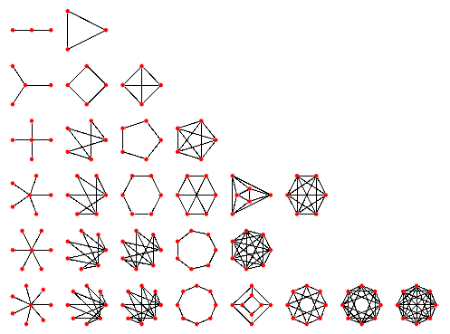
| شكل 9 – نمونههايي از گرافهاي «يال متقارن» (Edge Transitive). |
| |  گراف «يال متقارن» (Edge Transitive) گراف «يال متقارن» (Edge Transitive)
گراف  «يال متقارن» (Edge Transitive) است اگر براي هر دو يال «يال متقارن» (Edge Transitive) است اگر براي هر دو يال .gif) و و .gif) ، يك «عنصر» (Element) نظير: ، يك «عنصر» (Element) نظير: .gif) در در .gif) وجود داشته باشد بهگونهاي كه داشته باشيم: وجود داشته باشد بهگونهاي كه داشته باشيم:
(رابطهي 16) بهعبارت ديگر، يك گراف «يال متقارن» (Edge Transitive) است اگر گروه «همريختي» (Automorphism) آن براي يالهايش، متقارن عمل كند. يك «يال همريختي» (Edge Automorphism) يك گراف عبارت است از جايگشت يالهايي كه رابطهي «يال مجاورتي» (Edge- Adjacency) را حفظ كند.
 گراف «نيمهمتقارن» (Semisymmetric) . «متقارن» (Symmetric) گراف «نيمهمتقارن» (Semisymmetric) . «متقارن» (Symmetric)
يك گراف «منتظم» (Regular) كه «يال متقارن» (Edge Transitive) باشد ولي «رأس متقارن» (Vertex Transitive) نباشد گراف «نيمهمتقارن» (Semisymmetric) ناميده ميشود.
در عوض گرافي كه هم «يال متقارن» (Edge Transitive) و هم «رأس متقارن» (Vertex Transitive) باشد «گراف متقارن» (Symmetric) ناميده ميشود.
.gif)
| شكل 10 – گراف «صفر معمولي»
(صفر - Regular). | | .gif)
| شكل 11 – گراف «يك معمولي»
(1 - Regular). | | .gif)
| شكل 12 – گراف «دو معمولي»
(2 - Regular). | | .gif)
| شكل 13 – گراف «سه معمولي»
(3 - Regular). |
| |  گراف «منتظم» (Regular) گراف «منتظم» (Regular)
ياداوري – يك گراف «منتظم» (Regular) گرافي است كه هر رأس آن داراي تعداد همسايههاي يكساني باشد. بهعنوان مثال:
هر رأس گراف «منتظم» داراي «درجهي» يكساني است. يك گراف «منتظم» كه هر رأس آن داراي درجهي .gif) است گراف « است گراف «.gif) منتظم» (k-Regular) ناميده ميشود. منتظم» (k-Regular) ناميده ميشود. بنابراين گرافهاي «منتظم» با حداكثر درجهي 2 خيلي راحت طبقهبندي ميشوند:
|  گراف «صفر منتظم» (صفر - Regular) گراف «صفر منتظم» (صفر - Regular)
يك گراف «صفر منتظم» داراي رؤوس غيرمتصل (غيرهمبند) است.
| |  گراف «يك منتظم» (1 - Regular) گراف «يك منتظم» (1 - Regular)
يك گراف «يك منتظم» داراي يالهاي غيرمتصل (غيرهمبند) است.
| |  گراف «دو منتظم» (2 - Regular) گراف «دو منتظم» (2 - Regular)
يك گراف «دو منتظم» داراي حلقههاي غيرمتصل (غيرهمبند) است.
| |  يك گراف «سه منتظم» (3 - Regular) به گراف «مكعبي» (Cubic) شهرت دارد. يك گراف «سه منتظم» (3 - Regular) به گراف «مكعبي» (Cubic) شهرت دارد.
| |  يك گراف «اكيداً منتظم» (Strongly Regular) گرافي منتظمي است كه در آن هر زوج رأس مجاور داراي تعداد همسايههاي يكسان بوده و هر زوج رأسهاي غيرمجاور داراي تعداد يك گراف «اكيداً منتظم» (Strongly Regular) گرافي منتظمي است كه در آن هر زوج رأس مجاور داراي تعداد همسايههاي يكسان بوده و هر زوج رأسهاي غيرمجاور داراي تعداد .gif) همسايهي يكسان هستند. همسايهي يكسان هستند.
بهعنوان مثال:
از سادهترين گرافهايي كه «منتظم» (Regular) بوده ولي «اكيداً منتظم» (Strongly Regular) نباشند ميتوان به گرافهاي ذيل اشاره كرد:
براين اساس، يك گراف «كامل» (Complete) .gif) ، گرافي «اكيداً منتظم» (Strongly Regular) براي هر ، گرافي «اكيداً منتظم» (Strongly Regular) براي هر .gif) است. است. |
|
|
| ماتريسهاي «وقوع» (Incidence) و «مجاورت» (Adjacency) |
به هر گراف  يك ماتريس يك ماتريس .gif) نسبت داده ميشود كه ماتريس «وقوع» نسبت داده ميشود كه ماتريس «وقوع»  ناميده ميشود. رؤوس ماتريس ناميده ميشود. رؤوس ماتريس  را با را با .gif) و يالهاي آن را با و يالهاي آن را با .gif) نشان ميدهيم: نشان ميدهيم:
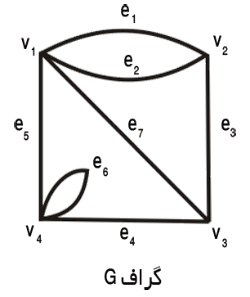 | شكل 14 – گراف  . . | | 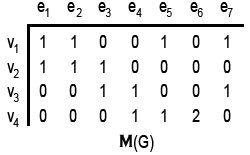
| شكل 15 - ماتريس «وقوع» گراف  . . | | 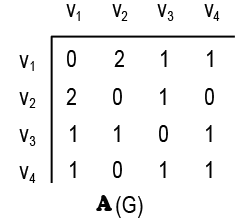
| شكل 16 - ماتريس «مجاورت» گراف  . . |
ماتريس «مجاورت» (Adjacency) يك گراف معمولاً كوچكتر از ماتريسهاي «وقوع» (Incidence) آن گراف بوده و گرافها در اين شكل هستند كه عموماً در كامپيوترها ذخيره ميشوند.
| موارد كاربرد ماتريسهاي «وقوع» (Incidence) و «مجاورت» (Adjacency) |
موارد ذيل را ميتوان نشان داد:
 زيرگراف (Subgraph) زيرگراف (Subgraph)
يك گراف .gif) زيرگراف زيرگراف  ناميده و بهصورت: ناميده و بهصورت: .gif) نوشته ميشود اگر داشته باشيم: نوشته ميشود اگر داشته باشيم:
 زيرگراف ويژه (Proper Subgraph) زيرگراف ويژه (Proper Subgraph)
زماني كه داشته باشيم:
| - .gif) | | - اما .gif) باشد، مينويسيم: باشد، مينويسيم: |
و چنين ميخوانيم:
| «.gif) يك زيرگراف ويژه از يك زيرگراف ويژه از  است». است». |
اگر .gif) يك زيرگراف از يك زيرگراف از  باشد باشد  يك «سوپرگراف» از يك «سوپرگراف» از .gif) يا «مافوق گراف» يا «مافوق گراف» .gif) است. است.
 «زيرگراف» يا «سوپرگراف» پوششي (Spanning Subgraph) (Spanning Supergraph) «زيرگراف» يا «سوپرگراف» پوششي (Spanning Subgraph) (Spanning Supergraph)
زيرگراف يا سوپرگراف پوششي (Spanning Subgraph) (Spanning Supergraph) از  ، يك زيرگراف (يا سوپرگراف يا مافوق گراف) از ، يك زيرگراف (يا سوپرگراف يا مافوق گراف) از .gif) است كه در آن داريم: است كه در آن داريم:
(رابطهي 18)
 گراف سادهي ضمني (Underlying Simple Graph) گراف سادهي ضمني (Underlying Simple Graph)
با حذف همهي حلقههاي گراف  براي هر زوج رؤوس مجاور - بهگونهاي كه يك اتصال بين رؤوس موجود باشد – يك گراف «سادهي ضمني» (Underlying Simple Graph) بهدست خواهد آمد (شكل 4). براي هر زوج رؤوس مجاور - بهگونهاي كه يك اتصال بين رؤوس موجود باشد – يك گراف «سادهي ضمني» (Underlying Simple Graph) بهدست خواهد آمد (شكل 4).
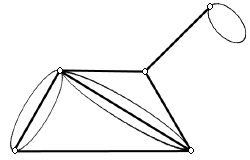
| شكل 17 – يك گراف و گراف
«سادهي ضمني» (Underlying Simple Graph).
| 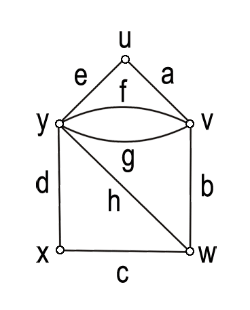
| شكل 18 – گراف  . . | | 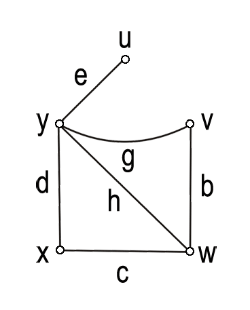
| شكل 19 – يك زيرگراف پوششي از  . . | | 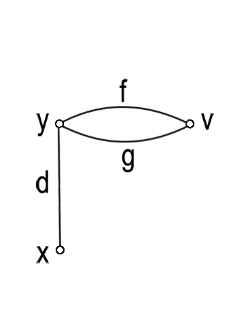
| شكل 20 - .gif) . . | | 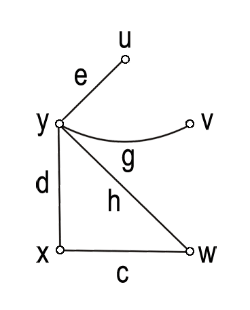
| شكل 21 - .gif) . . | | .gif)
| شكل 22 – يك زيرگراف القايي
(Induced Subgraph). | | .gif) | شكل 23 – زيرگراف القايي لبهدار
(The Edge-Induced Subgraph)
.gif) . . |
 زيرگراف القايي (Induced Subgraph) زيرگراف القايي (Induced Subgraph)
فرض كنيد .gif) يك زيرمجموعهي غيرتهي از يك زيرمجموعهي غيرتهي از .gif) باشد. زيرگراف باشد. زيرگراف  كه مجموعهي رؤوسش كه مجموعهي رؤوسش .gif) بوده و مجموعه يالهايش مجموعهي يالهاي گراف بوده و مجموعه يالهايش مجموعهي يالهاي گراف  باشد بهگونهاي كه يالهايش داراي دو سر در مجموعه رؤوس باشد بهگونهاي كه يالهايش داراي دو سر در مجموعه رؤوس .gif) باشد اصطلاحاً زيرگرافي از باشد اصطلاحاً زيرگرافي از  ناميده ميشود كه با ناميده ميشود كه با .gif) القا شده است و اينگونه نشان داده ميشود: القا شده است و اينگونه نشان داده ميشود:
زيرگراف القايي .gif) بهصورت ذيل نشان داده ميشود: بهصورت ذيل نشان داده ميشود:
زيرگراف القايي .gif) عبارت است از زيرگرافي كه با حذف رؤوس در عبارت است از زيرگرافي كه با حذف رؤوس در .gif) همراه با يالهاي وقوع آن از گراف همراه با يالهاي وقوع آن از گراف  بهدست ميآيد. بهدست ميآيد.
اگر .gif) براي براي .gif) مينويسيم: مينويسيم:
اكنون فرض كنيد .gif) يك زيرمجموعهي ناتهي از يك زيرمجموعهي ناتهي از .gif) باشد. زيرگراف باشد. زيرگراف  كه مجموعهي رؤوس آن مجموعهي انتهاي يالها در كه مجموعهي رؤوس آن مجموعهي انتهاي يالها در .gif) باشد اصطلاحاً زيرگراف باشد اصطلاحاً زيرگراف  ناميده ميشود كه با ناميده ميشود كه با .gif) القا شده و بهصورت ذيل نوشته ميشود: القا شده و بهصورت ذيل نوشته ميشود:
زيرگراف پوششي از گراف  با مجموعه يالهاي با مجموعه يالهاي .gif) بهصورت سادهي ذيل نوشته ميشود: بهصورت سادهي ذيل نوشته ميشود:
زيرگراف پوششي از گراف  زيرگرافي است كه با حذف يالها در زيرگرافي است كه با حذف يالها در .gif) از گراف از گراف  بهدست ميآيد. بهدست ميآيد. بهطور مشابه، گراف بهدست آمده از  با اضافه كردن يك مجموعه يال با اضافه كردن يك مجموعه يال .gif) بهصورت ذيل نوشته ميشود: بهصورت ذيل نوشته ميشود:
اگر داشته باشيم: .gif) ، بهجاي بهترتيب ، بهجاي بهترتيب .gif) و و .gif) مينويسيم: مينويسيم: .gif) و و .gif) . . در شكلهاي 5، 6، 7، 8، 9 و 10 چند نوع زيرگراف نشان داده شده است.
 زيرگراف «منفصل» (Disjoint Subgraph) زيرگراف «منفصل» (Disjoint Subgraph)
فرض كنيد .gif) و و .gif) زيرگرافهاي زيرگرافهاي  باشند. ميگوييم: باشند. ميگوييم:
 اجتماع زيرگرافها (Union) اجتماع زيرگرافها (Union)
اجتماع زيرگرافهاي .gif) و و .gif) - كه بهصورت ذيل نوشته ميشود: - كه بهصورت ذيل نوشته ميشود: .gif) - زيرگرافي است با: - زيرگرافي است با:
| - مجموعه رؤوس: .gif)
| | - و مجموعه يالهاي: .gif) . . |
اگر .gif) و و .gif) «منفصل» باشند گاهي اوقات اجتماع آنها را بهصورت: «منفصل» باشند گاهي اوقات اجتماع آنها را بهصورت: .gif) نشان ميدهند. نشان ميدهند.
 فصل مشترك زيرگرافها (Intersection) فصل مشترك زيرگرافها (Intersection)
فصل مشترك زيرگرافهاي .gif) و و .gif) - كه بهصورت ذيل نوشته ميشود: - كه بهصورت ذيل نوشته ميشود: .gif) - زيرگرافي است با: - زيرگرافي است با:
| - مجموعه رؤوس: .gif)
| | - و مجموعه يالهاي: .gif) . . |
اما در اين حالت زيرگرافهاي .gif) و و .gif) بايد داراي حداقل يك رأس مشترك باشند. بايد داراي حداقل يك رأس مشترك باشند.
| مواردي كاربردي از زيرگرافها (Subgraphs) |
ميتوان موارد ذيل را در مورد زيرگرافها اثبات كرد: | - هر گراف «ساده» (Simple) با .gif) رأس نسبت به زيرگراف رأس نسبت به زيرگراف .gif) «يكريخت» است. «يكريخت» است.
| | - هر زيرگراف «القايي» (Induced) از يك گراف «كامل» (Complete)، گرافي «كامل» است.
| | - هر زيرگرافي از يك گراف «دوبخشي» (Bipartite) خود گرافي «دوبخشي» است.
| | - فرض كنيم گراف  گرافي «ساده» بوده و گرافي «ساده» بوده و .gif) عددي صحيح باشد بهطوري كه داشته باشيم: عددي صحيح باشد بهطوري كه داشته باشيم:
(رابطهي 19) در اين صورت اگر .gif) باشد و همهي زيرگرافهاي القايي گراف باشد و همهي زيرگرافهاي القايي گراف  بر روي بر روي .gif) رأس تعدادي مساوي يال داشته باشند در اين صورت يكي از گزارههاي ذيل صحيح است: رأس تعدادي مساوي يال داشته باشند در اين صورت يكي از گزارههاي ذيل صحيح است:
(رابطهي 20)
(رابطهي 21)
|
درجهي .gif) (يا (يا .gif) ) يك رأس ) يك رأس .gif) در گراف در گراف  برابر تعداد يالهاي «وقوع» برابر تعداد يالهاي «وقوع»  با با .gif) است كه در آن هر «حلقه» شمارشگر دو رأس است. علايم است كه در آن هر «حلقه» شمارشگر دو رأس است. علايم .gif) و و .gif) بهترتيب بيانگر «مينيمم درجه» و «ماكسيمم درجهي» رؤوس گراف بهترتيب بيانگر «مينيمم درجه» و «ماكسيمم درجهي» رؤوس گراف  هستند. هستند. تعداد رؤوس گراف  را با را با .gif) نشان داده و «مرتبهي گراف» نشان داده و «مرتبهي گراف»  ميناميم. ميناميم. بهعنوان مثال: در شكل 10 «مرتبهي» گراف عدد 5 است. تعداد يالهاي گراف  را با را با .gif) نشان داده و «اندازهي گراف» نشان داده و «اندازهي گراف»  ميناميم. ميناميم. بهعنوان مثال: در شكل 10 «اندازهي» گراف عدد 4 است.
| قضيهاي دربارهي درجههاي رؤوس (Degree) |
ميتوان قضيهي ذيل را براي هر گراف نظير:  ثابت كرد: ثابت كرد: | جمع درجههاي همهي رؤوس يك گراف با دو برابر تعداد يالها آن برابر است.
(رابطهي 22) |
از اين قضيه ميتوان عبارت ذيل را نتيجه گرفت:
| در هر گراف، تعداد رؤوس با درجهي «فرد» عددي «زوج» است. |
بر اين اساس ميتوان تعريفهاي ذيل را ارائه داد:
| موارد كاربردي از «درجههاي رؤوس» (Degree) |
ميتوان موارد ذيل را نشان داد:
| مسيرها و همبندي (Paths and Connection) |
يك «گشت» (Walk) در گراف  يك دنبالهي محدود و غيرتهي يك دنبالهي محدود و غيرتهي .gif) است كه عبارتهايش متناوباً يال و رأس باشد بهگونهاي كه داشته باشيم: است كه عبارتهايش متناوباً يال و رأس باشد بهگونهاي كه داشته باشيم:
بدينترتيب گفته ميشود:
| - «گشت» .gif) از از .gif) تا تا .gif) | | - يا «گشت» .gif) . . |
همچنين ميتوان اصطلاحهاي ذيل را در ارتباط با «گشت» بهكار برد:
| - رؤوس .gif) و و .gif) بهطور نسبي با عنوان «ابتدا» و «انتهاي» بهطور نسبي با عنوان «ابتدا» و «انتهاي» .gif) | | - .gif) با عنوان «رؤوس دروني» (Internal Vertices) با عنوان «رؤوس دروني» (Internal Vertices) | | - عدد صحيح .gif) با عنوان «طول گشت». با عنوان «طول گشت». |
اگر .gif) و و .gif) «گشتهايي» باشند «گشت» «گشتهايي» باشند «گشت» .gif) با معكوس كردن با معكوس كردن .gif) بهدست آمده و با بهدست آمده و با .gif) مشخص ميشود. مشخص ميشود.
«گشت» .gif) با الحاق با الحاق .gif) و و .gif) در در .gif) بهدست آمده و با بهدست آمده و با .gif) نشان داده ميشود. نشان داده ميشود.
«بخشي» از «گشت» .gif) عبارت است از «گشتي» كه زيردنبالهاي از عبارت است از «گشتي» كه زيردنبالهاي از .gif) شامل عبارتهاي پيدرپي از «گشت» شامل عبارتهاي پيدرپي از «گشت» .gif) است. اصطلاحاً به آن بخش است. اصطلاحاً به آن بخش .gif) از «گشت» از «گشت» .gif) اطلاق ميشود. اطلاق ميشود. در يك گراف «ساده»، يك «گشت» .gif) با دنبالهي با دنبالهي .gif) از رؤوسش مشخص ميشود. علاوه بر آن حتي در گرافهايي كه «ساده» محسوب نميشوند گاهي اوقات بايد به دنبالهاي از رؤوس استناد كنيم كه عبارتهاي پيدرپي آن بهعنوان يك «گشت» مجاور هستند. در چنين حالتهايي فهميده ميشود كه بحث براي هر «گشتي» با رؤوس پيدرپي صادق است. از رؤوسش مشخص ميشود. علاوه بر آن حتي در گرافهايي كه «ساده» محسوب نميشوند گاهي اوقات بايد به دنبالهاي از رؤوس استناد كنيم كه عبارتهاي پيدرپي آن بهعنوان يك «گشت» مجاور هستند. در چنين حالتهايي فهميده ميشود كه بحث براي هر «گشتي» با رؤوس پيدرپي صادق است.
.gif)
| شكل 31 - «گشت» (uavfyfvgyhwbv)،
«گذر» (wcxdyhwbvgy)
«مسير» (xcwhyeuav). |
اگر علاوه بر آن، رؤوس .gif) «مجزا» باشند «مجزا» باشند .gif) «مسير» (Path) ناميده ميشود (شكل 16). «مسير» (Path) ناميده ميشود (شكل 16). ياداوري – از اصطلاح «مسير» (Path) همچنين براي گراف يا زيرگرافي استفاده ميشود كه يالها و رؤوسش برحسب يك «مسير» هستند.
.gif)
| شكل 32 – يك گراف همبند. | | .gif)
| شكل 33 – يك گراف غيرهمبند با سه جزو. | | .gif)
| شكل 34 - يك گراف غيرهمبند با سه جزو. |
دو رأس .gif) و و .gif) از گراف از گراف  «همبند» (Connected) گفته ميشود اگر يك مسير «همبند» (Connected) گفته ميشود اگر يك مسير .gif) در گراف در گراف  وجود داشته باشد. همبندي رابطهي همارزي در مجموعه رؤوس وجود داشته باشد. همبندي رابطهي همارزي در مجموعه رؤوس .gif) است. است. بنابراين شرط لازم و كافي براي آنكه بخشي از مجموعه رؤوس .gif) به زيرمجموعهي غيرتهي به زيرمجموعهي غيرتهي .gif) وجود داشته باشد آن است كه هر دو رأس وجود داشته باشد آن است كه هر دو رأس.gif) و و .gif) به يك مجموعه تعلق داشته باشد. به يك مجموعه تعلق داشته باشد. زيرگرافهاي .gif) «اجزاي» (Components) گراف ناميده ميشوند. اگر گراف «اجزاي» (Components) گراف ناميده ميشوند. اگر گراف  داراي دقيقاً يك «جزو» (Component) باشد گراف داراي دقيقاً يك «جزو» (Component) باشد گراف  «همبند» (Connected) است. در غير اينصورت، گراف «همبند» (Connected) است. در غير اينصورت، گراف  «غيرهمبند» (Disconnected) خواهد بود. «غيرهمبند» (Disconnected) خواهد بود. تعداد اجزاي گراف  با با .gif) مشخص ميشود (اشكال 31، 32 و 33). مشخص ميشود (اشكال 31، 32 و 33).
| كاربردهايي از مفاهيم مسيرها و همبندي (Paths and Connection) |
موارد ذيل را ميتوان دربارهي مفاهيم مسيرها و همبندي اثبات كرد: |