در نظریه گراف یک سری از گرافها وجود دارند که خاصند و بهدلیل خصوصیاتشان و طرز ساخت یا کاربردی ترکیبیاتی و غیره از اهمیت خاصی برخوردارند مانند گراف پترسون که حتما درمورد آن اطلاعاتی دارید. گراف کنزر یکی از این گرافهاست...
مقدمه
در نظریه گراف یک سری از گرافها وجود دارند که خاصند و به دلیل خصوصیاتشان و طرز ساخت یا کاربردی ترکیبیاتی و غیره از اهمیت خاصی برخوردارند مانند گراف پترسون که حتما درمورد آن اطلاعاتی دارید.
گراف کنزر یکی از این گرافهاست، این گرافها به نام مارتین کنزر نامگذاری شدهاند که
برای اولین بار آنها را در سال ۱۹۵۵ بررسی کرد.
این گراف که با KGn,k نشان داده میشود، گرافی است که رأسهای آن نظیر زیرمجموعههای k-عضوی از یک مجموعهی n-عضوی است.
بین دو رأس این گراف یک یال وجود دارد اگر و تنها اگر زیرمجموعههای نظیر رأسها ناسازگار باشند (اشتراکشان تهی باشد).
با توجه به روش ساخت یک گراف کنزر KGn,k بهسادگی میتوان به خصوصیات زیر اشاره کرد:
1. تعداد راسهای گراف کنزر برابر 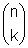 است.
است.
2. هر راس در گراف کنزر با 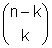 راس دیگر مجاور است.
راس دیگر مجاور است.
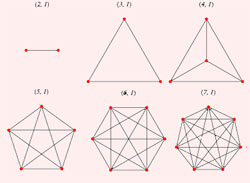
3. گراف کامل n-رأسی، گراف کنزر KGn,1 است و در شکل 1 هم مشاهده میشود.
 |
|
شكل 1 |
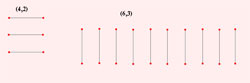
4. در گراف کنزر اگر k=n/2 باشد، و n هم عددی زوج باشد، آنگاه هر راس تنها با یک راس دیگر مجاور است و بنابراین گراف موردنظر شبیه نردبانی است که  پله دارد و در شکل 2 هم دو نمونه از این گرافها نشان داده شدهاند.
پله دارد و در شکل 2 هم دو نمونه از این گرافها نشان داده شدهاند.
 |
|
شكل 2 |
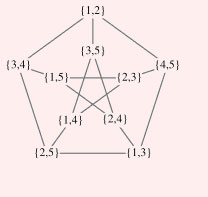
5. گراف کنزر KG5,2 با گراف پترسون ایزومورف است و در شکل 3 دیده میشود.
 |
|
شكل 3 |
6. کنزر حدس زده بود که عدد رنگی گراف KGn,k دقیقاً برابر n-2k+2 است. Lovasz در سال ۱۹۷۸ و Joshua در سال ۲۰۰۲ برای این فرمول اثباتهایی ارائه دادند و در سال ۲۰۰۴ Matoušek اثباتی کاملاً ترکیبیاتی برای آن پیدا کرد.
مطالعهي بيشتر: