در سالهای اخیر، تمرکز پژوهشگران بر روی توصیف ریاضیاتیِ شبکههای مختلف است.

- با چه احتمالی دو نفر که شما آنها را میشناسید ممکن است همدیگر را بشناسند؟
- مردم دنیا بهطور متوسط با چند نفر در ارتباط مستقیم و با چند نفر در ارتباط غیرمستقیم هستند؟
- کوتاهترین فاصلهی ارتباطی میان شما و فردی که هرگز ندیدهاید و نمیشناسید، چند نفر است؟
|
و یا پرسشهایی از این دست که:
- برای رسیدن از یک نقطهی شهر به نقطهی دیگر، کوتاهترین مسیر کدام است؟
- چطور میتوان ارتباط رشتههای بسیار زیاد و پیچیدهی عصبی موجود در بدن را، بررسی کرد؟
- آیا تاکنون چنین پرسشهایی برایتان پیش آمده؟
|
جستجوی پاسخ برای این قبیل پرسشها، شاخهی جدیدی از علم را پیش روی دانشمندان و پژوهشگران قرار داده که پایه و اساس آن در نظریهی گرافها نهفته است. این شاخه که امروزه بهسرعت در حال گسترش است و هر روز کاربردهای بیشتری پیدا میکند «علم شبکهها» یا «Networks science» نام دارد.
شبکه در حقیقت یک گراف جهتدار است که از تعدادی راس و یال تشکیل شده است. خیابانهای یک شهر یک شبکه است که میدانها رئوس و خیابانها و اتوبانها، یالهای آن هستند. رشتههای عصبی، سیستم ارتباطی رشتههای عصبی، مردم جامعه و ارتباطاتشان، شبکههای کامپیوتری و ... مثالهایی از شبکهها هستند.
رئوس (مجموعهی یک بعدی از نقاط)
یالها (مجموعهی دوبعدی از خطوط)
ماتریس همسایگی (ماتریس گراف متناظر با شبکه)
اندازه (تعداد رئوس شبکه)
راسها یا گرههایی که بهطور مستقیم با یک یال بهم متصل هستند را گرههای همسایه میگویند. همانطور که میدانیم درجهی هر راس تعداد یالهای متناظر با آن راس را مشخص میکند و اندازهی شبکه هم تعداد رئوس را. فاصلهی هر دو راس، کمترین تعداد یالهایی است که باید طی شود تا از یکی از راسها به دیگری برسیم. شعاع شبکه بیشترین فاصله میان دورترین دو راس متعلق به شبکه است. میانگین طول مسیر، میانگین فواصل بین هر دو راس متعلق به شبکه برای تمام جفتهای ممکن در شبکه است.
علم شبکه، شاخهای از علم است که بهدنبال اصول کلی، الگوریتمها و ابزارهایی است که رفتار شبکهها را کنترل میکنند. این شاخهی در حال رشد، به بررسی اتصالات میان شبکههای فیزیکی یا مخابراتی، بیولوژیکی و اجتماعی، میپردازد.
مطالعهی شبکهها برای تحلیل و بررسی دادههایی که ارتباطات پیچیدهای با هم داشتند، پدیدار شد. اولین مقالهای که در این زمینه به چاپ رسید، «پلهای هفتگانهی کونیگزبرگ» یا «Seven Bridges of Konigsberg» نام دارد که توسط «لئونارد اویلر» (Leonhard Euler)، در سال 1736 میلادی نوشته شد. توصیف اویلر از راسها و یالها پایهی نظریهی گراف است.
شهر کونیگزبرگ در روسیهی کنونی و در دو طرف رودخانهی پریگل (Pregel) قرار دارد که دو جزیرهی بزرگ را در بر میگیرد. این دو جزیره و قسمتهای دیگر شهر بوسیلهی هفت پل به هم متصل شده اند. مسالهای که در ابتدا مطرح شد این بود: پیدا کردن مسیری که تمام شهر را طی کند و از هر پل تنها و تنها یک بار بگذرد. اویلر ثابت کرد که چنین مسیری وجود ندارد. او ابتدا مساله را به یک گراف تبدیل کرد که چهار قسمت شهر، راسها و هفت پل متصل کنندهی آنها، یالها بودند. سپس اینگونه استدلال کرد: «هنگامی که از یک راس وارد یکی از پلها میشوید، از یک پل دیگر خارج شدهاید. به بیان دیگر، در حین طی شدن هر مسیری در گراف، تعداد دفعاتی که یک نفر وارد یک راس میشود برابر با تعداد دفعاتی است که یک نفر از آن راس خارج میشود. بنابراین تعداد پلهایی که به هر راس میرسند باید زوج باشد، حال آنکه برای همهی راسها، تعداد یالها فرد است.»
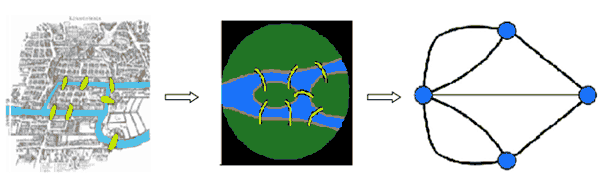
شیوهی حل این مساله، راهنمای بسیاری از مدلسازیها و روشهای تحلیلی بود، اما هنوز کاربردهای وسیع آن بهخوبی شناخته نشده بود.
در سال 1930 «ژاکوب مورنو» (Jacob Moreno) که یک روانشناس بود، نظریهی گرافها را بر روی یک سیستم اجتماعی بهکار برد و آغازگر تحلیل شبکههای اجتماعی شد. در این زمان، علم شبکهها وارد مرحلهای شد که اهمیت و میزان کاربرد آن در زمینههای مختلف بهخوبی برای همه آشکار شد. گام بعدی، ورود نظریهی احتمالات به نظریهی گرافها بود. «پاول اردوش» (Paul Erdos) این گام را برداشت.
در سالهای اخیر، تمرکز پژوهشگران بر روی توصیف ریاضیاتیِ شبکههای مختلف است. در این زمان مطالعات بر روی شبکه از حالت ساده و بدیهی گذشته خارج شده بود و شبکههای مورد بررسی اصطلاحا «شبکههای پیچیده» (complex networks) نامیده شدند. از ویژگیهای این شبکهها اینست که نه کاملا تصادفی هستند و نه کاملا منظم. تلاش برای شبیهسازی این شبکهها منجر به معرفی مدلهایی مانند «شبکهی دنیای کوچک» (small-world networks) توسط «دانکن واتز» (Duncan Watts) و شبکهی بیمقیاس یا (scale-free network) توسط «آلبرت لازلو باراباشی» (Albert-Laszlo Barabasi) شد. شکل زیر سه نمونه شبکه بهترتیب از سمت چپ، منظم، دنیای کوچک و تصادفی را نشان میدهد.
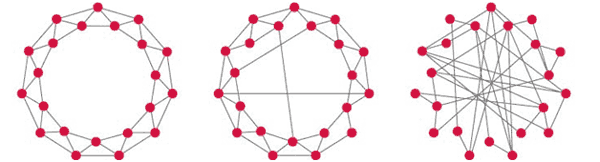
شبکه دنیای کوچک: مدلی از شبکه است که شبکههای واقعی زیادی را در بر میگیرد. ایدهی اولیهی این مدل زمانی بهوجود آمد که عدهای بهدنبال ساختن شبکههایی بودند که از قطع کردن بعضی از اتصالات و ایجاد اتصالات جدید در شبکههای منظم بهوجود آید. از ویژگیهای چنین شبکههایی این است که بیشتر راسها به هم متصل نیستند ولی تنها با چند گام میتوان به بیشتر راسها رسید.
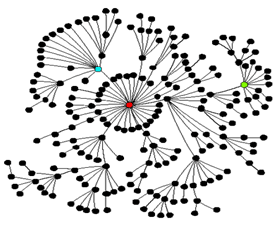
شبکه بیمقیاس: در این شبکهها، توزیع درجات راسها، توانی است. یعنی از رابطهی P(k)~k-γ پیروی میکنند. بههمین دلیل در این شبکهها، بیشتر راسها دارای درجات کمی هستند و تعداد کمی راس وجود دارد که درجاتشان زیاد است. شکل مقابل نمونهای از شبکههای بیمقیاس را نشان میدهد.