زنگتفریح شماره 140

معادلهی دیوفانتی x2-Dy2=1 ، که در آن D عدد صحیح غیرمربعی است، به این علت به معادلهی پل موسوم است که اویلر به اشتباه راهحل آن را به پل، ریاضیدان انگلیسی قرن هفدهم نسبت داده بود (این راه حل باید به براونکر منسوب میشد). معادلهی پل احتمالا معروفترین معادلهی دیوفانتی بعد از معادلهی مربوط به سه-تائیهای فیثاغورسی a2+b2=c2، و حتی از بعضی جهات، مهمتر از آن است. راه حل معادلهی پل مرحلهی اصلی در راه حل معادلهی دیوفانتی درجه دوم دو متغیره است. و نیز وسیلهی کلیدی اثبات قضیهی ماتیاسویچ، در این مورد که آلگوریتمی برای حل جمیع معادلات دیوفانتی موجود نیست، است. نظر به این موضوع، مناسب و ضروری بوده که معادلهی پل اولین ظهور خود را در اساس ریاضیات یونانی داشته باشد، و ملاحظهی این که چگونه یونانیان آن را درک کردند موثر و گیراست.
سادهترین مثال معادلهی پل x2-2y2=1 توسط فیثاغورسیان در رابطه با 2√ مورد مطالعه قرار گرفت. اگر x و yجوابهای بزرگ این معادله باشند، در این صورت x⁄y ≈ √2 و درواقع فیثاغورسیان طریقی برای تولید جوابهای بزرگتر و بزرگتر، به کمک روابط بازگشتی
xn+1=xn+2yn
yn+1=xn+yn
به دست آوردند. محاسبهای مختصر نشان میدهد که:
(xn+12 - 2yn+12= - (xn2-2yn2
در نتیجه، اگر (xn,yn) در x2 - 2y2 = ±1 صدق کند، (xn+1,yn+1) در x2 - 2y2 = ±1 صدق میکند. در این صورت، با آغاز از جواب بدیهی (x0,y0)=(1,0) معادلهی x2 - 2y2 = 1 ، جوابهای متوالیا بزرگتر (x4,y4)، (x2,y2)، ... را بهدست می آوریم.

اما روابط بازگشتی فوق برای اولین بار چگونه کشف شدهاند؟ واندرواردن [1976] و فاولر [1980, 1982]چنین مطرح میکنند که رمز این کار آلگوریتم اقلیدسی به کار رفته در قطعه خطها، عملی که یونانیان آن را تفریق نشانی مینامیدند، است. با مفروض بودن دو طول a و b، شخص میتواند دنبالهی (a2,b2)، (a1,b1)، .... را، با استفاده از تفریق مکرر طول کوچکتر از طول بزرگتر، تعریف کند. اگر a و b مضارب صحیح واحدی باشند، در این صورت جریان مورد بحث مختوم میشود، اما اگر b⁄a گنگ باشد، برای همیشه ادامه مییابد. میتوانیم به راحتی تصور کنیم که فیثاغورسیان به تفریق نشانی به کار رفته در مورد a=1، b=√2 علاقهمند بودهاند. این چیزی است که در این مورد رخ میدهد. a و b را با اضلاع یک مستطیل نمایش میدهیم، و هر تفریق عدد کوچکتر از عدد بزرگتر را با بریدن مربع مربوطه بر ضلع کوچکتر آن مطرح میکنیم (شکل 1). ملاحظه میکنیم که مستطیل باقیماندهی بعد از مرحلهی 2، با اضلاع
1-2√ و (1-2√)2√ = 2√-2،
به همان شکل مستطیل اصلی، با این تفاوت، است که ضلع بزرگتر آن در این حالت به جای این که افقی باشد قائم است. نتیجه میشود که مراحل مشابهی برای همیشه رخ میدهند، که در ضمن، اثبات دیگری در مورد این که 2√ اصم است، نیز هست. اما، توجه فعلی ما به رابطهی بین مستطیلهای مشابه متوالی است.

شکل 1
اگر فرض کنیم که ضلعهای بزرگتر و کوچکتر مستطیلهای مشابه متوالی yn+1، xn+1 و yn، xn باشند، میتوانیم، در مورد xn+1 و yn+1، رابطهی بازگشتی زیر را، با استفاده از شکل 2 استخراج کنیم:
xn+1 = xn + 2yn
yn+1 = xn + yn
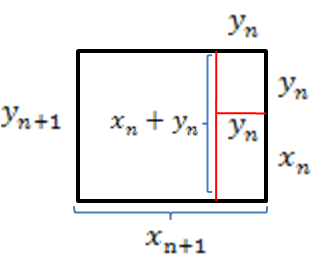
شکل 2
این روابط همان روابط فیثاغورسیانند، و تفاوتشان در این است که xn، yn مان اعداد صحیح نیستند، و در x2-2y2=0 و نه x2-2y2=1 صدق میکنند. با وجود این، شخص حس میکند که شکل 2 طبیعیترین تعبیر این روابط را به دست میدهد. ممکن است این حقیقت که روابط یکسانی جوابهای معادلات x2-2y2 = ±1 را تولید میکنند، به عنوان نتیجهای از این تمایل که آلگوریتم اقلیدسی با x1 = y1 =1 ختم شود، کشف شده باشد. اگر فیثاغورسیان با x1 = y1 = 1 آغاز کرده و رابطهای بازگشتی مورد بحث را به کار برده بودند، در این صورت، میتوانستند دریابند که (xn,yn) در x2-2y2 = (-1)n صدق میکند.
مثالهای بسیار دیگری ازمعادلهی پل x2-Dy2=1 در ریاضیات یونانی رخ میدهد. و آنها را میتوان به روشی مشابه، با استفاده از کاربرد تفریق نشانی در مستطیلی به اضلاع 1، D√ ، بررسی کرد. در قرن هفتم میلادی براهما گوپتا، ریاضیدان هندی، رابطهی بازگشتی برای تولید جوابهای x2-Dy2=1 بهدست داد. هندیها آلگوریتم اقلیدسی بر طولهای 1 و D√ ، را ذره ساز مینامیدند زیرا آلگوریتم مزبور قطعات مورد بحث را به تکههای کوچکتر و کوچکتر تجزیه میکند. برای بهدست آوردن رابطهای بازگشتی شخص باید بداند که نهایتا مستطیلی متناسب با مستطیل اصلی باز میگردد، حقیقتی که تنها در سال 1768 توسط لاگرانژ به دقت اثبات شد. کارهای بعد اروپائیان در مورد معادلات پل، که در قرن هفدهم با براونکر و دیگران آغاز شد، مبتنی بر کسر مسلسل مربوط به D√ بود، گرچه این روش نیز به همان روش تفریق نشانی منجر میشود. در مورد تاریخ متراکم اما مفصل معادلهی پل مورد زیر را ملاحظه کنید:
Dickson [1920], pp. 341-400
جنبهی جالب نظریهی مورد بحث همان رابطهی نامنظم بین D و تعداد مراحل تفریق نشانی قبل از بازگشت مستطیلی متناسب با مستطیل اصلی است. اگر تعداد مراحل مزبور زیاد باشد کوچکترین جواب غیر بدیهی x2-Dy2=1 بسیار بزرگ است. یکی از مثالهای مشهور این مورد مسالهی موسوم به مسالهی رمهی ارشمیدس (287-212 ق. م.) است. این مساله به معادلهی
x2 - 4729494y2 = 1
منجر میشود که کوچکترین جوابش که توسط امثور بهدست آمده دارای 206545 رقم است!
غلامرضا پورقلی
دانشجوی دکتری ریاضی
دانشگاه تهران