الگوریتمی جدید برای درخت پوشا با کم‌ترین هزینه با استفاده از جستجوی ژرفایی در گراف غیرجهت‌دار

این الگوریتم جدید برای مسأله‌ي درخت پوشا با کم‌ترین هزینه در هر گراف غیر جهت‌دار ارائه شده است. در این الگوریتم از هیچ‌گونه الگوریتم Sort یا صف اولویت (Priority Queue) یا پشته‌ی دودویی (Binary Heap) استفاده نشده است.
این الگوریتم بر پایه‌ی جستجوی ژرفایی (DFS) و حذف سنگین‌ترین یال دیده شده دایره در DFS است. این الگوریتم در بدترین حالت، برای گرافی با 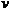راس و 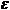 یال زمان  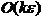را می‌گیرد (در مورد نماد O در زنگ تفریح مر بوط به پیچیدگی الگوریتم‌ها توضیح داده شده است) که در آن:

مشهورترین الگوریتم‌ها برای حل مسأله‌ي «درخت پوشا با کم‌ترین هزینه»، «الگوریتم کروسکال» (Kruskal) و «الگوریتم پریم» (Prim) می‌باشند. این الگوریتم‌ها یک روش ابتکاری برای بهینه‌سازی ارائه دادند که به آن Greedy Strategy  (یا همان حریصانه كه در زنگ تفریح‌های نوروزی در مورد آن توضیح لازم داده شده است) می‌گویند. در هر مرحله از الگوریتم، یکی از چندین انتخاب‌ها باید ساخته شود.

Greedy Strategy از انتخابی که در لحظه، بهترین است دفاع می‌کند. هر الگوریتم به آسانی در زمان 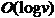 با استفاده از پشته‌ی دودویی معمولی آماده برای اجرا می‌شود.

با استفاده از «پشته‌ي فیبوناچی» (Fibonacci Heap) می‌توان سرعت الگوریتم پریم (Prim) را افزایش داد تا در مدت 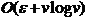 اجرا شود.

این الگوریتم که ارائه شده (DHEA)، استراتژی مشابهی دارد که از DFS پیروی می‌کند و آن این است که گراف را به‌صورت ژرفایی جستجو می‌کند. هنگامی که دایره دیده شد سنگین‌ترین یال در دایره حذف می‌شود. این فرایند تا زمانی ادامه پیدا می‌کند که جستجوی ژرفایی پایان یابد. این الگوریتم زمان 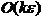   را می‌گیرد جایی که k تعداد یال‌های بازگشت (Back Edges) در DFS است. بر حسب خصوصیات گراف:

در نتيجه این الگوریتم می‌تواند برای گراف‌هایی که اختلاف تعداد رؤوس و یال‌های آن‌ها کوچک است، مناسب باشد.

در پایان باید به این مطلب اشاره داشت که نویسندگان مقاله مزبور سرکار خانم دکتر هایده اهرابیان و هم‌چنین جناب آقای دکتر عباس نوذری دالینی از اساتید دانشکده ریاضی ، آمار و علوم رایانهِ دانشگاه تهران هستند.
این زنگ تفریح در واقع بهانه‌ای است مناسب برای شما تا سعی کنید با فعالیت‌های علمی آنان بیش‌تر آشنا شوید .