زنگتفریح شماره ۱۱۳
در
زنگتفریح شماره ۱۰۲ مختصری با نظریهی گرهها آشنا شدهاید. در واقع نظریهی گرهها به مطالعهی خمهای بسته در فضای سه-بُعدی میپردازد. شاید گرهها با توجه به پیشرفتهای زیادی که در هندسه بهوجود آمده است موجوداتی ساده بهنظر برسند، ولی در واقع اینگونه نیست. هنوز پاسخی کامل برای اینکه آیا دو گره با هم «همارز» هستند یا نه پیدا نشده است. بهطور شهودی دو گره را همارز گویند اگر بدون پاره کردن، بتوان یک گره را به گره دیگر تبدیل کرد.
ریاضیدانان برای مطالعهی گرهها، با ساختن «ناوردا»های (Invariants) مختلف آنها را به شاخهها و شیهای مختلف ریاضیات ربط میدهند. منظور ما از ناوردا یک تناظر بین گرهها با موجودات دیگر ریاضی است به طوری که به هر دو گره همارز، دقیقا یک موجود را نسبت دهیم. از جمله ناورداهایی که تاکنون برای مطالعهی گرهها استفاده شده است میتوان به گرافها، گروهها، رویهها، عددها، چندجملهایها و غیره نام برد. اما چگونه برای یک گره ناوردا بسازیم.
درسال ۱۹۲۶ میلادی، کورت رایدمایستر (Kurt Reidemeister)، ریاضیدان آلمانی، قضیهای را اثبات کرد که اکنون ریاضیدانان آن را بهعنوان قضیهای بنیادی در نظریهی گرهها میشناسند. قبل از اینکه قضیهی رایدمایستر را بیان کنم، ابتدا با حرکتهای رایدمایستر آشنا شوید:
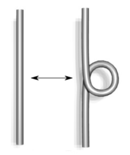 |
 |
| حرکت رایدمایستر نوع اول |
حرکت رایدمایستر نوع دوم |
 |
| حرکت رایدمایستر نوع سوم |
بهصورت شهودی خیلی راحت میتوان حدس زد هیچ یک از سه حرکت زیر تاثیری در یک گره نخواهد داشت. اما آنچه که رایدمایستر اثبات کرد بیشتر از این بود:
| قضیهی رایدمایستر: |
|
هر دو گره همارز با تعدادی از حرکتهای رایدمایستر قابل تبدیل به هم هستند.
|
به عنوان مثال میتوان دید که گره «هشت» با «تصویر آینهای» خود همارز است:
اگر ما بخواهیم یک ناوردا برای گرهها بسازیم کافیست آن را فقط برای این سه حرکت امتحان کنیم. در زنگتفریح بعدی یک ناوردای ساده برای گرهها میسازیم.