اين ساده است كه يك مستطيلي با اضلاع و قطرهايي با اعداد تام پيدا كنيم؟ اين يك مسأله قديمي مستطيل‌هاي فيثاغورث است و اين يك مسأله شناخته شده از زمان قديم است كه چطور همه آن‌ها ‌را پيدا كنيم.

اگر از راه‌حل كلاسيك استفاده كنيم، پيدا كردن يك مكعب مستطيل كامل سخت نيست.اما هنوز كسي نتوانسته است كه يك مكعب كامل پيدا كند كه قطر بزرگ هم كه بين دو زاويه مقابل به هم هستند اعداد تام باشند.

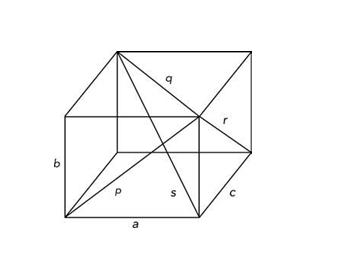
 با علامت‌گزاري روي شكل و با توجه به فيثاغورث، بايد a،b،c را پيدا كنيم و چهارعدد تام در تساوي‌هاي زير باشند:

a²þ b²= p²

a²þ c²= q²

b²þ c² = r²

a²þ b²þ c² = s²

وجود يا عدم وجود همچين اعدادي هنوز ثابت نشده است اما حدس‌هاي نزديكي زده شده است:

a ¼ 240;   b ¼ 117;   c ¼ 44;     p ¼ 267;  q ¼ 244;   r ¼ 125

اما s عدد صحيح نيست.

a ¼ 18; 720;  b ¼ 211;773; 121; c ¼ 7;800;   p ¼ 23; 711;

q ¼ 20;280;              r ¼ 16;511;              s ¼ 24; 961;

اما b يك عدد صحيح نيست.

اگر مكعب كاملي هم وجود داشته باشد، از اعداد بزرگي تشكيل شده است. ثابت شده است كه كوچكترين ضلع آن بايد حداقل 2³²¼ 4;294; 967;296 باشد.