زنگتفریح شماره ۱۶۱

|
مسالهی زیر را ریاضیدان هلندی فرانسیس واناسخوتن (معروف به اسخوتن جوان) (1615-1660) حل کرده است:
اگر مثلث ABC طوری در صفحه حرکت کند که A و B به ترتیب در امتداد خطهای m و n حرکت کنند، مکان C چیست؟
|
راه حل او بسیار هوشمندانه است. ما ابتدا یک قضیهی مقدماتی را ثابت میکنیم:
اگر خط راست l طوری حرکت کند که دو نقطه روی آن A و B به ترتیب در امتداد دو خط راست متعامد ثابت حرکت کنند، مکان هر نقطهی سومی روی l یک بیضی است.
اثبات
دو خط متعامد ثابت را محور x و محور y میگیریم. وقتی l حرکت میکند، نقطهی A همواره روی محور x است و نقطهی B روی محور y. نقطهی سوم روی خط متحرک را با P(x, y) و زاویهی متغیر OAB را با φ نشان میدهیم (شکل ۱). اگر P بین A و B باشد، آنگاه:
(۱) 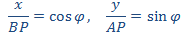
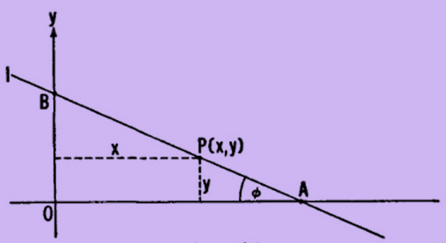
شکل ۱
اگر P بین A و B نباشد، عبارات (۱) باز هم مقادیر صحیح مختصات x و y را به دست میدهند ولی علامتهای آنها ممکن است تغییر کند. در هرصورت، مجذور کردن فرمولهای 1 نتایجی به دست میدهد که به ازای همهی موقعیتهای P برقرار است، یعنی:
(۲) 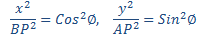
درنتیجه به دست میآوریم:
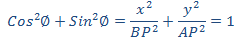
یعنی مکان P بیضیای است که مرکزش در مبدا است و نیم قطرهای آن BP و AP به ترتیب روی محورهای x و y اند.
حال فرض کنیم که راسهای A و B از مثلث ABC مقید به حرکت روی دو خط، به ترتیب، m و n هستند که با یکدیگر زاویهی α میسازند (شکل ۲) میخواهیم مکان راس سوم C را تعیین کنیم.
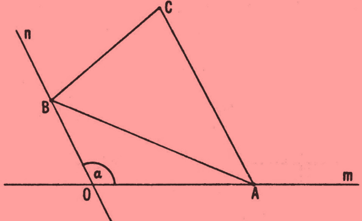
شکل ۲
وقتی B روی n به سمت O حرکت میکند، A از O دور میشود و مثلث AOB دائما تغییر میکند. ولی در این حین، دایرههای محیطی مثلثهای AOB همگی به یک اندازهاند. در هر دو مورد، وتر AB هیچگاه تغییر نمیکند و تنها یک دایره وجود دارد که در آن وتری به طول AB میتواند قطعهای را جدا کند که زاویهی آن برابر α است. البته، مکان این دایره همراه با مکان وتر AB تغییر میکند.
پس فرض کنید مکان خاصی، مثلا آنکه با خط پر در شکل ۳ نشان داده شده، انتخاب کنیم و دایره محیطی مثلث AOB را رسم کنیم. دایره محیطی در هر مکان دیگری، مثلا با خط چین نشان داده شده، به همان اندازهی دایره محیطی قبلی است و چون طول AB تغییر نمیکند، موقعیت دایره و مثلث نسبت به هم نیز در جریان حرکت پیشگفته بیتغییر میماند. مانند این است که دایره به مثلث چسبیده باشد و این دو با هم حرکت کنند. در نتیجه حرکتهای A و B باعث میشوند که مثلث و دایره به هم چسبیده طوری حرکت کنند که نقطه O همواره روی محیط دایره باشد. میتوان تصور کرد شکل طوری حرکت میکند که کمان دایره درخور نقطهی O است و نقاط A و B برخطهای m و n میلغزند.
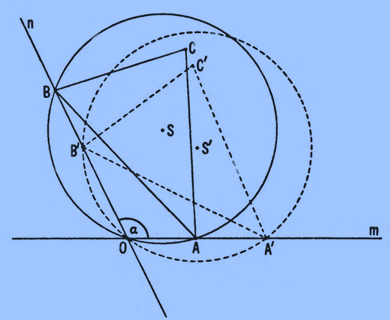
شکل ۳
پس از آنکه B از O میگذرد، وتر AB در مقابل زاویهی مکمل α قرار میگیرد. ولی این همان زاویهی مربوط به قطعهی دیگر دایره چسپیده به مثلث است. پس درست وقتی که B (و بعدا A) در جریان حرکت خود از O میگذرد، دایره از O میگذرد. شکل ۴ را ببینید.
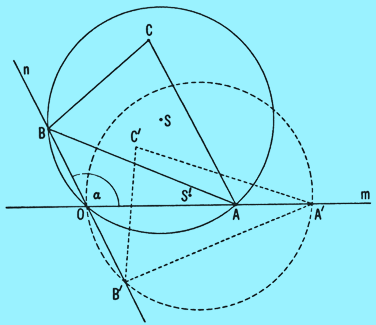
شکل ۴
به دایرهی متحرک و مثلث چسپیده به آن، خط واصل راس C و مرکز دایره، S را اضافه میکنیم و نقاط تلاقی آن را با دایره، U و V مینامیم (شکل ۵). وقتی دایره حرکت میکند، نقاط U ،B ،A و V همراه با آن حرکت میکنند.
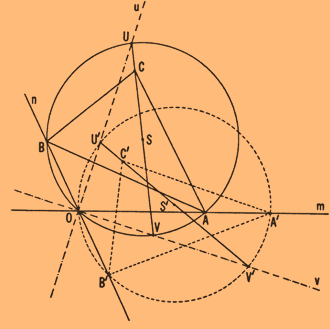
شکل ۵
قوس AU که روبهروی AOU∢ است، بدون تغییر حرکت میکند. بنابراین، AOU∢ در جریان حرکت تغییر نمیکند و چون ضلع OAی آن روی خط m میماند، ضلع دیگرش که نقطهی ثابت O را به نقطه متحرک U وصل میکند باید ثابت بماند. پس نقطهی U در امتداد خطی مانند u به سوی O حرکت میکند.
همینطور، V در امتداد خطی چون v حرکت میکند. همچنانکه B و A در امتداد خطهای خود m و n سیر میکنند، نقاط U و V روی خطهای u و v سیر مینمایند.
چون UV قطری از دایره است، VOU∢ یک زاویهی قائمه است. یعنی، خطهای u و v بر هم عمودند. پس وقتی A و B در امتداد m و n حرکت میکنند، U و V روی جفتی از خطهای عمود بر هم حرکت میکنند. راس C روی خط گذرنده از U و V است و بنابراین طبق حکمی که در آغاز بیان کردیم، C روی بیضی به مرکز O حرکت میکند که اقطارش روی u و v قرار دارند و نصف طولهای آنها به ترتیب CV و CU است.
نتیجه میگیریم که وقتی مثلثی چنان حرکت کند که هر یک از دو راسش روی خط راستی حرکت کند، راس سومش یک بیضی را میپیماید.