ابتدا لازم است از «اصل برتراند» و «قضيهي چبيشف» برايتان بگوييم: «براي هر عدد صحيح .gif) حداقل يك عدد اول بين حداقل يك عدد اول بين 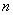 و و .gif) موجود است». موجود است». يا بهقول رياضيداني بهنام «ن. ج. فاين» (N. J. Fine):�«چبيشف» اين مطلب را گفت ولي من آن را دوباره ميگويم؛ هميشه يك عدد اول بين 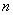 و و .gif) وجود دارد. وجود دارد. براي كسب اطلاعات بيشتر راجع به اين اصل و قضيه ميتوانيد به وبسايتها بهنشاني ذيل و يا متون استاندارد «نظريهي اعداد» مراجعه فرماييد:
ابتدا يك مثال سادهاي بزنيم تا براي بحث در مورد جواب انگيزهي لازم را داشته باشيم:
فرض كنيد ميخواهيم اعداد 1 تا 8 را بهصورت زوجهاي مرتبي دراوريم كه جمع هر دو عدد «اول» باشد. ياداوري ميكنيم كه بين 8 تا 15 دو عدد اول وجود دارد كه عبارتاند از: 11 و 13. عدد 13 را در نظر ميگيريم. جمع زوجهاي .gif) برابر عدد 13 است. بدينترتيب تمام اعداد در زيرمجموعهي 5 تا 8 را بهطور كامل استفاده كردهايم. برابر عدد 13 است. بدينترتيب تمام اعداد در زيرمجموعهي 5 تا 8 را بهطور كامل استفاده كردهايم. بنابراين كافي است زوجهاي باقيمانده از اعداد 1 تا 4 را بيابيم. اين مثالي است از اينكه يك «استدلال استقرايي» چگونه در حل مسائل ميتواند مفيد باشد.
اما براي حل مسألهي اصلي از «استقرا» استفاده ميكنيم: براي شروع اثبات از طريق «استقرا»، ابتدا از حالت .gif) (با اعداد صحيح 1 و 2) آغاز ميكنيم. بهسادگي درمييابيم براي (با اعداد صحيح 1 و 2) آغاز ميكنيم. بهسادگي درمييابيم براي .gif) و و .gif) جمع اعداد 1 و 3 خواهد شد كه عددهايي اول هستند. جمع اعداد 1 و 3 خواهد شد كه عددهايي اول هستند. سپس اثبات ميكنيم كه حكم براي 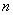 از 1 تا از 1 تا .gif) نيز صادق است. بهعبارت: نيز صادق است. بهعبارت: «فرض كنيد براي هر 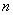 از 1 تا از 1 تا .gif) اعداد صحيح اعداد صحيح .gif) ميتواند به زوجهايي نظير: ميتواند به زوجهايي نظير: .gif) تقسيم شود بهگونهاي كه براي هر تقسيم شود بهگونهاي كه براي هر .gif) جمع دو عدد يعني: جمع دو عدد يعني: .gif) عددي «اول» باشد. عددي «اول» باشد. از فرض براي حالت .gif) استفاده ميكنيم. يعني بايد زوج اعداد از 1 تا استفاده ميكنيم. يعني بايد زوج اعداد از 1 تا .gif) داراي اين ويژگي باشند. با استفاده از «اصل برتراند» مطمئن هستيم بين داراي اين ويژگي باشند. با استفاده از «اصل برتراند» مطمئن هستيم بين .gif) و و .gif) عدد اولي نظير: عدد اولي نظير: .gif) وجود دارد. وجود دارد. لذا داريم:
(رابطهي 1)
از رابطهي 1 رابطهي ذيل را درمييابيم:
(رابطهي 2)
لذا زوجهاي ذيل داراي جمع .gif) هستند: هستند:
(رابطهي 3)
توجه كنيد كه جمع ارقام هر زوج همان عدد .gif) بوده و همهي اعداد صحيح از بوده و همهي اعداد صحيح از .gif) تا تا .gif) استفاده شدهاند. استفاده شدهاند. از آنجايي كه .gif) و نهايتاً و نهايتاً .gif) نيز اعدادي «زوج» هستند فرض استقرا ميتواند براي زوجهاي اعداد از 1 تا نيز اعدادي «زوج» هستند فرض استقرا ميتواند براي زوجهاي اعداد از 1 تا .gif) نيز بهكار رفته و بدينترتيب حكم ثابت ميشود. نيز بهكار رفته و بدينترتيب حكم ثابت ميشود. |