چرا روز نجومي كوتاهتر از روز خورشيدي است؟
چرا روز خورشيدي ثابت نيست؟
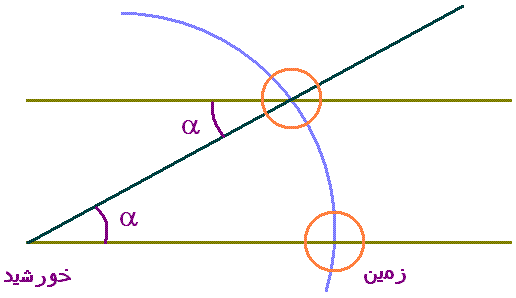
زمين تقريباً در هر 365 روز يكبار به دور خورشيد ميگردد، يعني تقريباً روزي ْ1 . بنابراين، با توجه به شكل، براي آنكه دو بارِ پياپي خورشيد در صفحهي نصفالنهاري P قرار گيرد، زمين بايد تقريباً 1 درجه بيشتر بچرخد.
بنابراين روز خورشيدي كمي بلندتر از روز نجومي است. دقيقتر محاسبه ميكنيم. فرض كنيم «طول روز خورشيدي» t باشد. در يك روز خورشيدي زمين به اندازهيΩt در مدارش حركت كرده. در اينجاΩ «سرعت زاويهاي حركت مداريِ زمين» است. صفحهي نصفالنهاري P، در يك روز خورشيدي بهاندازهي wt چرخيده، كه بايد برابر باشد با 2π + Ωt، بنابراين:
| wt = 2π + Ωt → 2π/t = w - Ω |
داريم:
w = 7.292115 × 10-5 Rad/s , Ω = 1.991 × 10-7 Rad/s → t = 86400 s |
اگر مدار زمين به دور خورشيد دقيقاً «دايره» بود، آنوقت «بردار حامل زمين»، يعني برداري كه مركز خورشيد را به مركز زمين وصل ميكند، در زمانهاي مساوي زاويههاي مساوي ميپيمود، و طول روز خورشيدي ثابت ميبود.
اما مدار زمين «بيضي» است و بنابر «قانون دوم كپلر»، «بردار حامل زمين» در زمانهاي مساوي مساحتهاي مساوي جارو ميكند. وقتي زمين به حضيضاش نزديكتر است، «سزعت زمين» و در نتيجه «سرعت زاويهاي»اش بيشتر است، بنابراين «طول روز خورشيدي» بزرگتر ميشود، زيرا Ω بزرگتر ميشود.
اگر خوب دقت كنيد ميبينيد كه اين استدلال وقتي درست است كه «محور چرخش وضعي زمين» بر «صفحهي مداري زمين» عمود باشد. اما چنين نيست. اين باعث ميشود «طول روز خورشيدي» دقيقاً آنچه در بالا بهدست آورديم نباشد.
براي آنكه قانع شويم اين زاويه تأثير دارد، خوب است وضعيت عجيب ذيل را نگاه كنيم. اگر محور چرخش وضعي زمين در صفحهي مداري زمين بود چه ميشد؟ بايد دقت كنيم كه چون «تكانهي زاويهاي وضعي زمين» ثابت است و چون زمين را «كره» فرض كرديم، «بردار سرعت زاويهاي وضعي زمين» ثابت است، يعني همواره بهسمت يك ستارهي ثابت است. موضع اين ستاره با گذشت زمان تغيير نميكند.
اين براي موقعي كه «بردار سرعت زاويهاي زمين» در صفحهي مداري زمين هم باشد درست است، و در اين صورت در يك لحظهي خاص از سال، قطب شمال درست بر خط واصل مركز زمين به مركز خورشيد قرار ميگيرد. در اين صورت با آنكه زمين در اين روز خاص از سال هم به دو رمحور قطبياش ميچرخد، خورشيد در آسمانِ زمين ثابت ميماند. به اين ترتيب ميبينيم كه در اين موقع خاص از سال روز خورشيدي زياد ميشود.
«محور قطبي زمين» با «صفحهي مداري زمين» زاويهاي دارد كه تقريباً برابر است با ْ45/23 (يادآوري ميكنم كه منظور از زاويهي بردار a با يك صفحهي ∑ زاويهي a است با بردارn كه بر ∑ عمود است). ميتوان اين زاويه را در نظر گرفت، و طول روز خورشيدي را حساب كرد. نتيجه اين ميشود كه مقداري كه بالاتر بهدست آورديم، «ميانگين روز خورشيدي» است.