مسابقه شماره ۲۱۵

روی تختههای کلاسهای اول و دوم ۱۰۰ عدد زیر نوشته شدهاند.
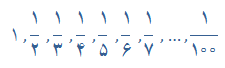
طناز دانشآموز کلاس اول و فرناز دانشآموز کلاس دوم هستند. این دانشآموزان در کلاس خود هر بار دو عدد دلخواه مانند a و b را پاک میکنند و بهجای آن عدد a+b+ab را مینویسند. این کار را آنقدر ادامه میدهند که فقط یک عدد باقی بماند.

طناز و فرناز از کلاس بیرون میآیند و عددی را که بهدست آوردهاند را اعلام میکنند، و با تعجب درمییابند که هر دو به یک عدد رسیدهاند، در حالیکه در انتخاب عددها و پاک کردن آنها از هم بیاطلاع بودهاند.
آیا میتوانید بگویید آن عدد چیست؟
البته پیدا کردن آن عدد ساده است، کافیست یک بار این کار را انجام دهید تا شما هم به این پاسخ یکتا برسید. پرسش اصلی این است که چرا هر بار که این کار را انجام میدهیم به این عدد میرسیم.
