زنگتفریح شماره ۱۵۲

مرد بزرگ دير وعده ميدهد و زود انجام ميدهد.
کنفوسيوس
بازیهایی وجود دارند که در بعضی موارد ریاضیات زیبایی در آنها نهفته است. یکی از این بازیها بازی ویتوف است که در این مقاله به آن خواهیم پرداخت. برای ورود به بحث به نتیجهای از قضیهی زیر از سام بیتی (Samuel Beatty (1881–1970) نیاز داریم:

(Samuel Beatty (1881–1970
قضیه: فرض کنید X عدد گنگ مثبت و Y عکس آن باشد. در این صورت، دو دنبالهی
1+X, 2(1+X), 3(1+X),…
و
1+Y, 2(1+Y), 3(1+Y),…
همراه با هم دقیقا یک عدد از بازههای (n,n+1) بین اعداد صحیح مثبت متوالی n=1,2,3,4,… را در بر دارند.
در سال 1927 اثبات زیبایی از این قضیه توسط اوستروسکی و آیتکن ارایه شده است. اثبات مقدماتی و قابل دستیابی است و برای خونندهی علاقمند فرصتی است تا خود به دنبال آن باشد.
نتیجهی سادهی زیر از این قضیه مورد نیاز است:
نتیجه: دنبالههای [n(1+X)] و [n(1+Y)] که به دنبالههای بیتی متناظر با با عدد گنگ X موسوماند، همراه با هم هر عدد طبیعی را دقیقا یک بار در بر دارند.
جفتهای از دنبالهها را که دارای این ویژگی (هر عدد طبیعی را دقیقا یک بار در بر دارند) هستند، مکمل مینامند.
در سال 1907 ریاضیدانی به نام ویتوف یک بازی ابداع کرد. که در آن دو نفر بازی میکنند و هریک به نوبت کبریتهایی از دو دسته کبریت برمیدارند. در آغاز، هر یک از دو دسته کبریت، تعداد دلخواهی کبریت دارد، مثلا یکی m چوب کبریت و دیگری n چوب کبریت. جریان این بازی را میتوانیم به وسیلهی جفتهای (a,b) تعقیب کنیم که نشاندهندهی تعداد کبریتهای باقیمانده در هر یک از دو دسته، پس از انجام هر حرکت، هستند. به این ترتیب، بازی با جفت (m,n) آغاز میشود.

Willem Abraham Wythoff (1865-1939)
قواعد این بازی ایجاب میکنند که هر حرکت از یکی از سه نوع زیر باشد:
برداشت کبریت از دستهی I
برداشت کبریت از دستهی II
برداشت کبریت از هر دو دسته، به تعداد مساوی از هر دسته.
بیان جبری این قاعدهها به صورت زیر است: جفت (m,n) به یکی از جفتهای زیر تبدیل میشود
(i) (m-t,n), (ii) (m,n-t), (iii) (m-t,n-t)
در همهی حالات، t≥1، زیرا دست کم یک کبریت برداشته میشود. تعداد کبریتهایی که برداشته میشوند به میل بازیکن بستگی دارد. بازیکن اگر بخواهد میتواند تمام دسته کبریت را بردارد. برنده کسی است که آخرین کبریت را بردارد.
به عنوان نمونه، یک بازی میتواند به این ترتیب باشد:
بعد از اینکه A بازی کرد A به (13، 16) میرسد، B بازی میکند و (19، 12) حاصل میشود.
A بازی میکند و (5، 9) حاصل می شود، B بازی میکند و (6، 2) حاصل میشود.
A بازی میکند و (1، 2) حاصل می شود، B بازی میکند و باید به یکی از حالات (1، 1)، (1، 0)، (0، 2) یا (0، 1) دست یابد.
A بازی میکند و به (0، 0) میرسد و برنده میشود.
توجه کنید جفت (1، 2) که A در حرکت ما قبل آخر خود به آن دست یافت، یک موقعیت برنده است زیرا صرفنظر از اینکه B کدام یک از چهار حرکت ممکن را انجام میدهد، A میتواند در حرکت بعدی برنده شود.
به طور کلی ما جفتی چون (a, b) را به عنوان موقعیت برنده برای بازیکن A تعریف میکنیم اگر استراتژی وجود داشته باشد که صرفنظر از هر حرکتی که B بعد از موقعیت (a, b) انجام دهد، A بتواند بازی را (نه لزوما در یک حرکت) ببرد. مثلا (1، 2) در بازی بالا یک موقعیت برنده است. هر چهار حرکت مجاز از (1، 2)، به موقعیتهای بازنده برای B میانجامد. یعنی به موقعیت-هایی که حریف میتواند با حرکت از آنجا بازی را ببرد.
اگر با موقعیت برندهی نهایی (0، 0) آغاز کنیم، میتوانیم فهرستی از تمام موقعیتهای برنده در بازی ویتوف به دست آوریم و به این منظور مثلا تمام جفتهای (x, y) را برای x+y=1,2,… بررسی میکنیم. به این طریق، میتوان نشان داد که همهی جفتهای (x, y) یا موقعیتهای برندهاند یا موقعیتهای بازنده. ولی معلوم شده است که از این فرایند خسته کننده میتوان کاملا صرف نظر کرد. خود ویتوف همهی موقعیتهای برنده را به وسیلهی یک فرمول مشخص کرد. و در بقیهی این نوشتار مشخصات مجموعهی W را از همهی جفتهای برنده را عرضه میکنیم و با نشان دادن اینکه هر حرکت از موقعیتی متعلق به W به موقعیتی میانجامد که در W نیست، ثابت خواهیم کرد که اعضای W واقعا موقعیتهای برنده هستند، و حرکتی وجود دارد که با آن حرکت از موقعیتی که در W نیست به موقعیتی در W میرسیم.
قضیه. موقعیتهای برنده را جفتهای (0, 0) و (an,bn ) که n=1,2,… معین میکنند، که در آن {an} و {bn} دنبالههای بیتی متناظر با عدد گنگ زیرند.
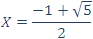
ملاحظه میکنیم که X همان میانگین طلایی معروف است و داریم:
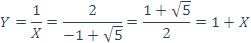
نکته: میانگین طلایی، نسبت عرض مستطیل طلایی به طول آن است. به عبارت دیگر، این نسبت برابر است با جواب مثبت معادلهی 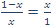 یعنی جواب مثبت معادلهی x2 + x - 1 = 0.
یعنی جواب مثبت معادلهی x2 + x - 1 = 0.
قرار میدهیم:
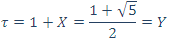
و در مییابیم که:
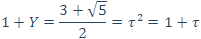
و دنبالههای بیتی متناظر، [n(1+X)] و [n(1+Y)] عبارتند از:
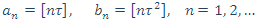
اگر (x,y) جفتی در W باشد (x,y) نیز چنین است، زیرا ترتیبی که برای دو دسته کبریت قائل میشویم، اهمیتی ندارد. مناسبتر این است که عدد کوچکتر جفت را با an نشان دهیم و جفت را به صورت (an,bn) بنویسیم یعنی an را اول بیاوریم.
اثبات این قضیه از حوصلهی بحث خارج است. اما از نتیجهی قضیهی بیتی بایست استفاده کرد. کماکان این کار به خوانندهی کنجکاو واگذار میشود.
این قضیه بیان میکند که همواره حرکتی مجازی وجود دارد که جفت غیر برندهای را به جفت برندهای تبدیل کند.