آگوست فرديناند موبيوس (August Ferdinand Möbius) در روز ۱۷ نوامبر ۱۷۹٠ در شهر زاکسن به دنيا آمد. وي رياضيدان و ستاره شناس مشهور آلماني است. بيشترِ شهرت او به دليل کشف نوار موبيوس است.

نوار موبيوس نواري است که دو لبة آن بر هم قرار گرفته و حلقه‌اي را به وجود مي‌آورد؛ البته بايد يک لبة انتهايي قبل از اتصال به لبة ديگر نيم دور چرخانده شود. اين نوار را دو رياضيدان آلماني به نامهاي آگوست فرديناند موبيوس و جان بنديکت (Johann Benedict) در سال ۱۸۵۸ به طور مستقل و جداگانه کشف کردند و به ثبت رساندند.
 

◄ روش ساخت نوار موبيوس:

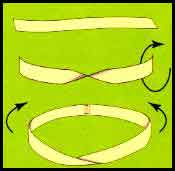
ابتدايي‌ترين راه براي ايجاد اين نوار، انتخاب يک نوار مستطيل شکل، دراز و نرمي است که آن را يک بار مي‌پيچانيم و سپس دو انتهاي آن را به هم متصل مي‌کنيم. سطحي که به اين ترتيب به دست مي‌آيد «نوار موبيوس» ناميده مي‌شود.
 

اين سطح تنها يک رو دارد. به بيان ديگر، يک صفحة کاغذي را مي‌توان با دو رنگ گوناگون در دو طرف آن رنگ کرد اما نوار موبيوس را با اين روش نمي‌توان با دو رنگ مختلف رنگ کرد. در صورت اقدام به چنين کاري به همان جايي که رنگ کردن را در ابتدا آغاز کرده‌ بوديم، مي‌رسيم؛ در حالي که در طرف ديگر نوار هستيم! پس نوار موبيوس، سطحي است که يک رو دارد و حرکت ما روي آن تا بينهاِت بار تکرار مي شود.
 

◄ تعريف خاص رياضي:

دليل «يک رويه بودن» اين نوار آن است که در هر نقطة مانند a از نوار موبيوس مي‌توان دو بردار با جهت‌هاي مختلف رسم کرد که بر نوار موبيوس در اين نقطه عمود باشد.

اين بردارها را قائم‌هاي نوار موبيوس در نقطة a مي‌ناميم. يکي از اين بردارها را انتخاب و نقطة a را به تدريج روي نوار موبيوس جابجا مي‌کنيم. در اين صورت بردار ما هم همراه با نقطه a جابجا مي‌شود. بنابراين، روي نوار موبيوس چنان مسير بسته‌اي وجود دارد که اگر قائمي اين مسير را روي سطح بپيمايد، به جاي اين که به وضع نخستين خود برسد، روي برداري که در جهت مخالف وضع نخستين آن است قرار مي‌گيرد.

 ◄ تعريف مرز يک ناحيه در فضا:
مرزِ يک ناحيه، خط جدا کنندة آن ناحيه از ناحية ديگر است. در رياضيات براي يک سطح سه مفهوم تعريف مي شود:
۱- نقطة داخلي: نقطه اي که بتوان آن را داخل يک دايره روي سطح محصور کرد.
۲- نقطة خارجي: نقطه اي است که بتوانيم دايره اي حول آن رسم کنيم که متعلق به آن سطح نباشد.
۳- نقطة مرزي: نقطه اي است که هر دايره اي حول آن رسم شود، قسمتي از آن متعلق به سطح و قسمت ديگر آن متعلق به خارج آن سطح باشد.
با اين تعريف نوار موبيوس فقط يک مرز دارد. يعني با يک بار حرکت در کرانه هاي انتهاي نوار تمام مرز آن را مي توانيم طي کنيم.
◄ نکات جالب درباره نوار موبيوساگر با يک خودکار بر روي نوار موبيوس خطي در طول نوار بکشيم و ادامه دهيم اين خط دوباره به نقطة شروع باز مي‌گردد و هر دو طرف نوار خط کشيده مي‌شود! در واقع، نوار موبيوس مثالي از يک روية بدون جهت (جهت ناپذير) است. يعني نوار موبيوس سطحي است که يک رو دارد. از خواص حيرت آور اين نوار آن است که اين نوار فقط يک مرز دارد.
 

نوار موبيوس خواص غيرمنتظرة ديگري نيز دارد؛ براي نمونه، هرگاه بخواهيم اين نوار را در امتداد طولش بِـبُريم به جاي اين که دو نوار به دست بياوريم، يک نوار بلندتر و با دو چرخش به دست مي آوريم! همچنين با تکرار دوبارة اين کار دو نوار موبيوس در هم پيچ خورده به دست مي‌آيد. با ادامة اين کار يعني بريدن پياپي نوار، در انتهاي کار تصاوير غيرمنتظره‌اي ايجاد مي‌شود که به حلقه‌هاي پارادروميک (paradromic rings) موسومند. همچنين اگر اين نوار را از يک سوم عرض نوار ببريم، دو نوارِ موبيوس در هم گره شده با طولهاي متفاوت به دست خواهيم آورد. تمامي اين کارها به آساني قابل اجراء هستند.
  

کاربرد خواص نوار موبـيوس در معماري

خاصيت موبيوسي: خاصيتي است که رابطة بين «درون» و «بيرون» را وارونه مي‌کند. يعني هر نقطه از يک سطح موبيوسي در عين حال که درون است، بيرون نيز مي‌باشد! بنابراين در يک تغيير پيوسته، نوعي دگرگوني در ماهيت يک فضا صورت مي‌گيرد. در واقع در اين حالت فضا خاصيت دو گانه اما پيوسته پيدا مي‌کند.
 

خاصيت موبيوس که گذر از درون به برون و از برون به درون را ممکن مي‌کند، کمابيش توانسته است بر فراز شکاف حاصل از دوگانگي (ثنويت) پلي بزند (شايگان،۱۳۸٠). بنابراين، فضاي ِميان «برون و درون»، «پيوستگي» و «تکرار» با يک تعريف رياضي به يک سطح هندسي تبديل مي‌شود. سطحي که بر آن در هر لحظه اي هم داخل و هم خارج فضا هستيم. اين ويژگي در طراحي معماري مورد توجه قرار گرفته است.

ساختار هندسي نوار موبيوس، «درون و بيرون» با «داخل و خارج» را تلفيق مي‌کند و فضاي سومي با کيفيتي جديد به وجود مي‌آورد. اين فضاي سوم، فضايي است که «همزماني»، «تبديل» و «تکرار» در ميان پديده ها در آن رخ مي‌دهد.