اگر بخواهیم بر اساس تعریف کتاب درسی (هندسه ۱) ده-ضلعی منتظمی رسم کنیم تنها به یک جواب خواهیم رسید. چرا بر اساس این تعریف هر چندضلعی باید یک خم «سادهٔ» بسته باشد.

اما اگر به تعریفی که در ویکی‌پدیای فارسی  آمده مراجعه کنیم، با دنیای بزرگ‌تری از چندضلعی‌ها روبه‌رو خواهیم شد. زیرا شرط «ساده» بودن در این تعریف لحاظ نشده است. پس با توجه به این تعریف ما دو ده-ضلعی منتظم می‌توانیم داشته باشیم که در شکل‌های زیر دیده می‌شوند. در این تصویر شعاع دایرهٔ محیطی هر دو ده-ضلعی با هم برابرند. در واقع محیط دایره را به ۱۰ کمان برابر تقسیم کرده‌ایم. سپس در سمت چپ هر نقطهٔ تقسیم را با پاره‌خطی به نقطهٔ مجاورش وصل کرده‌ایم و در شکل سمت راست هر نقطهٔ تقسیم را با پاره‌خطی به نقطهٔ سوم بعد از آن متصل کرده‌ایم.  

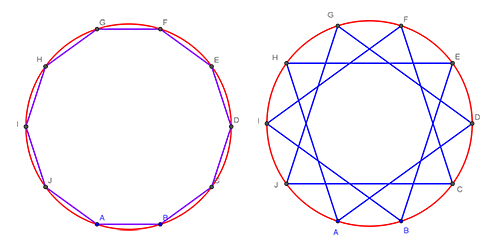
سوال مسابقهٔ ما در مورد این دو ده-ضلعی است: