زنگتفریح شماره ۱۴۹

 |
پیروزی یعنی خواستن
(ناپلئون بناپارت)
|
| قضیه ۱: هرگاه روی هریک از ضلعهای مثلث و در بیرون آن، سه مثلث چنان رسم کنیم که مجموع زاویههای راسهایی از آنها که غیر مجاور مثلث مفروض است برابر با ۱۸۰ درجه باشد، دایرههای محیطی این مثلثها در یک نقطه مشترکند. |
این قضیه که دربارهی خطهای متقارب است، اثباتی ساده دارد. بنا به شکل ۱، روی ضلعهای مثلث ABC و در بیرون آن، مثلثهای ACQ ،CBP و BAR را چنان رسم کردهایم که مجموع سه زاویهی Q ،P و R برابر ۱۸۰ درجه است. دایرههای محیطی دو مثلث CBP و ACQ که در C مشترکند در نقطهی دیگر F نیز مشترکند. از F به سه نقطهی B ،A و C وصل میکنیم. هریک از چهار گوشههای FBPC و FCQA محاطی است و با توجه به اینکه در هر گوشهی محاطی زاویههای مکملند، میتوانیم بنویسیم:
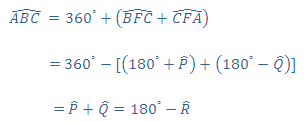
بنابراین چهار گوشهی ARBC محاطی است و دایرهی محیطی مثلث ABR از F میگذرد.
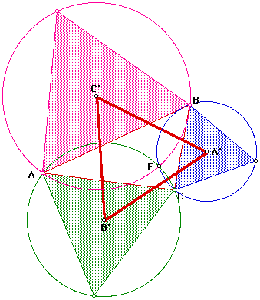
شکل ۱
دو حالت خاص این قضیه، به صورت زیر است.
| قضیه ۲: هرگاه راسهای B ،A و C از مثلث ABC بهترتیب روی ضلعهای RP ،QR و PQ از مثلث PQR واقع باشند، دایرههای محیطی مثلثهای ACQ ،CBP و BAR در یک نقطه مشترکند. |
| قضیه ۳: هرگاه روی ضلعهای مثلث ABC و در خارج آن سه مثلث متشابه CQA ،PCB و BAR را بسازیم (که در تشابه آنها زاویههای Q ،P و R متناضر نیستند)، دایرههای محیطی سه مثلث مزبور در یک نقطه مشترکند. |
از قضایای فوق نتیجهی زیر را داریم.
| قضیه ۴: هر گاه چهار خط دوبهدو در شش نقطهی B1 ،A1 ،C ،B ،A و C1 متقاطع باشند به گونهای که ABC1 ، AB1C ،A1BC و A1B1C1 نقطههای بر یک استقامت را مشخص میکنند، دایرههای محیطی چهار مثلث AB1C1، A1B1C1 ،ABC1 و ABC در یک نقطه مشترکند. |
از قضیهی ۳ نتیجهی مهمی به دست میآید که به مثلث حاصل از O2 ،O1 و O3 مرکزهای دایرههای محیطی سه مثلث CAQ ،BCP و ABR مربوط است (شکل 1). ضلعهای O2O3، O3O1 و O1O3 از این مثلث به ترتیب بر وترهای مشترک (محورهای اصلی) دوبهدو از دایرهها عمودند و زاویههای O2 ،O1 و O3 از این مثلث به ترتیب با زاویههای Q ،P و Rبرابرند. با توجه به اینکه این زاویهها، زاویههای غیرمتناظر از مثلث متشابهند، پس:
|
قضیهی ۵: هرگاه روی ضلعهای مثلث ABC و در خارج آن سه مثلث متشابه CQA ،PCB و BAR را بسازیم (زاویههای متناظر بهترتیب نامگذاری مثلثها هستند)، مرکزهای دایرههای محیطی این مثلثها، مثلثی تشکیل میدهند که با آن مثلثها متشابه است.
|
حالت خاص این قضیه را به صورت زیر بیان میکنیم:
| قضیهی ۶: هرگاه روی اضلاع یک مثلث و در خارج آن سه مثلث متساویالاضلاع بسازیم، مرکزهای دایرههای محیطی این مثلثها نیز یک مثلث متساویالاضلاع تشکیل میدهند. |
از قرار معلوم، ناپلئون بناپارت تا اندازهای ریاضیدان بوده و بهویژه علاقهای وافر به هندسه داشته است. میگویند پیش از آنکه حکومت فرانسه را در دست گیرد با ریاضیدانان نامی لاگرانژ و لاپلاس جلسات بحث و گفت و گو داشته است. حتی اینکه این لاپلاس یک بار بهطور جدی به او گفته است: "ژنرال، درسی از هندسه، آخرین چیزی است که از شما مورد تمنا است". لاپلاس بعدها مهندس نظامی مخصوص امپراطوری شد.
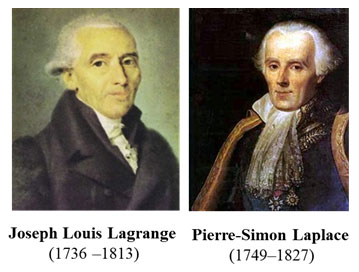
قضیهی ۶ را به ناپلئون نسبت میدهند، اما در این باره میتوان شک داشت، زیرا معلومات هندسی او آن اندازه نبوده که به این نتیجهی جالب توجه دست یابد: چنانکه در انگلیسی جملهی دوسویهی زیر را به او نسبت میدهند: Able was I ere I saw Elba
(تقریبا به این مضمون: "قبل از دیدن جزیرهی آلب میتوانستم").
به هر ترتیب، در حالتی که مثلثهای متساویالاضلاع بنا نهاده شده روی اضلاع مثلث را در خارج مثلث در نظر بگیریم آنگاه مثلث متساویالاضلاع به دست آمده از مرکزهای دایرههای محیطی این سه مثلث را مثلث ناپلئون خارجی نظیر آن مثلث گوییم (شکل ۲، مثلت به رنگ قرمز مثلث ناپلئون خارجی است)،
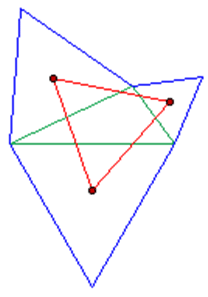
شکل ۲
و در حالتی که مثلثهای متساویالاضلاع را، مانند شکل ۳، در داخل مثلث بسازیم آنگاه مثلث متساوی الاضلاع (اثبات اینکه این مثلث متساویالاضلاع است جالب، آموزنده و البته ساده است و از خواننده خواسته میشود آن را به عنوان تمرینی ساده اثبات کند) به دست آمده از مرکزهای دایرههای محیطی این سه مثلث، مثلث ناپلئون داخلی نظیر این مثلث نامیده میشود (شکل ۳، مثلت به رنگ قرمز مثلث ناپلئون داخلی است) .
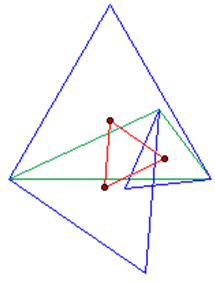
شکل ۳
بنابراین مطابق تعریف ارایه شده قضیهی ۶ به صورت زیر نیز قابل بیان است:
مثلث ناپلئون خارجی نظیر هر مثلث، متساویالاضلاع است.
همچنین قضیهی زیر را داریم:
| قضیهی ۷: مثلث ناپلئون داخلی هر مثلث متساویالاضلاع است. |
نتیجهی جالب و مهم زیر را میتوان به آسانی ثابت کرد:
| نتیجه: تفاضل مساحتهای دو مثلث ناپلئون خارجی و داخلی نظیر هر مثلث برابر است با مساحت آن مثلث. |