زنگتفریح شماره ۱۶۸
در عالم ریاضیات مجموعه کانتور یکی از مهمترین مجموعههایی است که برای آزمایش نظریههای جدید یا به عنوان مثال نقض برای گزارههای مختلف به کار میرود. این مجموعه معمولا به دو شکل معرفی میگردد.
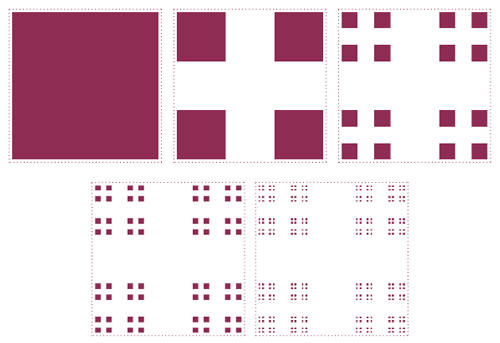
پارهخط واصل بین ۰ تا ۱ را فرض کنید. منظورمان دقیقا بازهٔ بسته [0,1]⊆R (وجود نقاط انتهایی بازه بسیار مهم است) است. یکسوم میانی این بازه را حذف کنید. یعنی بازه باز (13,23) را از [0,1] بردارید. چیزی که باقی میماند مجموعه [0,13]∪[23,1] است. از وسط هر دو بازه حاصل شده، یکسوم میانیشان را حذف کنید. نتیجه مجموعه [0,19]∪[29,13]∪[23,79]∪[89,1] است. اگر برای همه بازههای تولیدشده یکسوم میانیشان را حذف کنید و این کار را تا بینهایت (برای هر بازهای که در هر مرحله ایجاد میشود)، مجموعه حاصل همان مجموعه کانتور است. در شکل زیر ۶ مرحله از حذف یکسومهای میانی نمایش داده شدهاند.

شاید به این فکر بیافتید که اگر عمل حذف را تا بینهایت ادامه دهید چیز خاصی باقی نمیماند. ولی دقت کنید که نقاط 0، 13، 23 و 1 و نقاط ابتدایی و انتهایی همه بازههایی که در این مراحل ایجاد میشوند، هرگز حذف نشده و در مجموعه پایانی(مجموعه کانتور) حضور دارند. در حقیقت ما عمدا تصمیم گرفتیم که نقاط ابتدایی و انتهایی بازهها را حدف نکنیم. اما ماجرا به همین جا ختم نمیشود. اعضای مجموعه کانتور فقط یک سری نقطه نیستند؛ بلکه مجموعه کانتور شامل کلّی نقطه است. تعداد نقاط ابتدایی و انتهایی که در مجموعه کانتور هستند شماراست، ولی اگر بخواهیم در مورد تعداد کل نقاط مجموعه کانتور صحبت کنیم، این نقاط به تعداد ناشمارا هستند. برای اینکه در مورد تعداد اعضای مجموعه کانتور واضحتر صحبت کنیم، به تعریف این مجموعه به روشی دیگر میپردازیم.
روش دوم تعریف مجموعه کانتور کمی پیچیدهتر ولی بسیار دقیقتر است. ما معمولا برای بیان اعداد از دستگاه دهگانی (بر پایه ۱۰) استفاده میکنیم. یعنی اعداد ۰، ۱، ۲، ۳، ۴، ۵، ۶، ۷، ۸ و ۹ را داریم و بقیه اعداد را از ترکیب این ۱۰ رقم میسازیم. حال به نوشتن اعداد در پایه ۳ (دستگاه سهگانی) میپردازیم. یعنی ما فقط اعداد ۰، ۱ و ۲ را داریم و بقیه اعداد را با ترکیب این اعداد میسازیم. برای مثال نمایش اعداد ۰ تا ۱۰ دستگاه دهگانی در دستگاه سهگانی به این شکل است: ۰، ۱، ۲، ۱۰، ۱۱، ۱۲، ۲۰، ۲۱، ۲۲، ۱۰۰ و ۱۰۱. برای استفاده آسان از این دستگاه میتوانید به راحتی از روش تغییر مبنا که در کتب درسی آمده است استفاده کنید.
با توضیحات بالا، مجموعه کانتور، مجموعه اعداد بین ۰ و ۱ است که نمایش آنها در دستگاه سهگانی شامل ۱ نباشد. یعنی در نمایش این اعداد فقط رقمهای ۰ و ۲ ظاهر شوند. برای مثال عدد صفر و عدد 0.22222…≈1 (مثل 0.9999…≈1) در مجموعه کانتور هستند. تصور مجموعه کانتور در دستگاه سهگانی کاملا طبیعی و گویا است. بهعنوان مثال، برای حذف یکسوم میانی از بازه اولیه [0,1] کافی است اعدادی را بعد از ممیز (در دستگاه سهگانی) عدد ۱ دارند را حذف کنید و برای مرحله دوم؛ حذف یکسوم میانی بازههای [0,13] و [23,1] اعدادی را که در جایگاه دوم بعد از ممیز (در دستگاه سهگانی) رقم ۱ دارند را حذف کنید و این رویّه را همینطور تا بینهایت ادامه دهید تا مجموعه کانتور حاصل شود.

در مورد مجموعههای شمارا (شمارشپذیر) بهطور خلاصه توضیح میدهیم. مجموعه اعداد طبیعی N را فرض کنید. ما میتوانیم اعضای این مجموعه را (به ترتیب) بنوسیم یا به اصطلاح آنها را فهرست کنیم. فهرست کردن یک مجموعه یک بیان نادقیق از شمارایی است. تعریف دقیق آن بدین شکل است که مجموعه X شمارا (شمارشپذیر) میگوییم اگر یک تابع دوسویی (یکبهیک و پوشا) از X به N یا یک زیر مجموعه از N وجود داشته باشد. با این تعبیر مجموعه N مرجع شمارایی است. با روشی تکنیکی میتوان نشان داد که Q مجموعه اعداد گویا نیز مجموعهای شماراست.
ممکن است به این فکر کنید که تعداد اعداد گویا بسیار بیشتر از تعداد اعداد طبیعی است، ولی واقعیت آن است که یک تابع دوسویی از Q به N وجود دارد. R مجموعه اعداد حقیقی، شمارا نیست (پس مجموعههایی را که شمارا نباشند، ناشمارا مینامیم)، یعنی هیچ تابع دوسویی از R به N وجود ندارد. پس با اینکه تعداد هر دو مجموعه N و R نامتناهی است، ولی تعداد اعضای R بیشتر است. با یک روش تکنیکی نه چندان دشوار در آنالیز ریاضی میتوان نشان داد که تعداد اعضای مجموعه کانتور ناشمارا و در حقیقت برابر با تعداد اعضای R است.
در این جا به چند ویژگی بسیار جالب و مهم مجموعه کانتور میپردازیم.
اول آنکه تعداد اعضای این مجموعه ناشماراست ولی این مجموعه شامل هیچ بازهای نیست. چرا که اگر بازهای در این مجموعه وجود داشت باید یک سوم میانی آن را حذف و این کار را تا بینهایت ادامه میدادیم.
دوم؛ اگر اندازه بازههایی که حذف میکنیم را حساب کنیم:
با جمع کردن این اندازه ها داریم:
که برای محاسبه مجموع فوق دقت کنید که ما مجموع یک سری هندسی با جمله اولبه ۱/۳ و با قدر نسبت ۲/۳ را حساب کردیم. نتیجه آن است که از بازه [0,1] که اندازه آن ۱ است مجموعههایی را حذف کردیم که مجموع اندازههای آنها ۱ بود ولی تعداد نقاط باقیمانده از بازه [0,1] که آن را مجموعه کانتور نامیدیم، با تعداد نقاط مجموعه R (و همینطور مجموعه [0,1]) برابری میکند.
مراجع: