يكي از مهمترين نامساويها در رياضي، «نامساويها در مثلث» است. «نامساوي در مثلث» از يك نگاه عام بر روي فاصله بين نقاط متمركز بوده و عبارت است از اينكه خط مستقيم بين نقاط 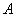 و و .gif) از جمع فواصل نقطهي از جمع فواصل نقطهي 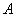 تا تا .gif) و و .gif) تا تا 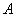 از هر مسيري كمتر است. اين امر بديهي بخشي از بهاصطلاح بينش روزانهي ما است و يادگيري آن ساده بوده اما در عين حال بسيار كاربردي است. از هر مسيري كمتر است. اين امر بديهي بخشي از بهاصطلاح بينش روزانهي ما است و يادگيري آن ساده بوده اما در عين حال بسيار كاربردي است. گاهي وقتي سخن از «نامساويها در مثلث» ميآيد بهياد نامساوي مربوط به اضلاع و زواياي مثلث نظير موارد ذيل ميافتيم:
| - در هر مثلث، ضلع روبهرو به زاويهي بزرگتر از ضلع روبهرو به زاويهي كوچكتر داراي بزرگي بيشتري است | | - در هر مثلث، مجموع هر دو ضلع از اندازهي ضلع ديگر بزرگتر است. | | - اندازهي تفاضل دو ضلع در هر مثلث از ضلع سوم كوچكتر است. | | - و ... |
در اين زنگ تفريح ضمن بيان روابط رياضي مربوط به نامساويهاي ذكر شده در مثلث (همراه با ذكر قضيههاي مربوط) به بيان يك «نامساوي بزرگتر در مثلث!» هم ميپردازيم.
در پايان از يكي از محققان رياضي و طراحان سؤالهاي المپياد جهاني رياضي سخن خواهيم گفت.
با فرض .gif) و و .gif) بهعنوان اعدادي حقيقي، بهعنوان اعدادي حقيقي، .gif) بيانگر عدد مربوط به فاصله بين دو نقطهي بيانگر عدد مربوط به فاصله بين دو نقطهي .gif) و و .gif) است؛ بنابراين دو حالت ممكن است: است؛ بنابراين دو حالت ممكن است: | - اگر .gif) داريم: داريم:
(رابطهي 1)
| | - اگر .gif) داريم: داريم:
(رابطهي 2) |
بنابراين ميتوان نتيجه گرفت:
(رابطهي 3)
گاهي اوقات ميتوان رابطهي 3 را با نماد ذيل نشان داد:
(رابطهي 4)
بديهي است براي هر سه نقطه نظير: .gif) ، ، .gif) و و .gif) ميتوان نامساويهاي ذيل را نوشت: ميتوان نامساويهاي ذيل را نوشت:
(رابطهي 5)
رابطهي فوق به «نامساوي در مثلث» (The Triangle Inequality) مشهور است. براي اثبات رابطهي 5 دو حالت را در نظر ميگيريم: - حالت اول - .gif)
در صورت وجود حالت اول، سه حالت ديگر ممكن است: |  .gif) و و .gif) در اين حالت داريم:
(رابطهي 6)
همچنين داريم:
(رابطهي 7)
در نتيجه داريم:
(رابطهي 8)
| | | |  .gif) و و .gif)
در اين حالت داريم:
(رابطهي 9)
همچنين داريم:
(رابطهي 10)
در نتيجه داريم:
(رابطهي 11)
| | | |  .gif) و و .gif)
در اين حالت داريم:
(رابطهي 12)
و همچنين داريم:
در نتيجه داريم:
(رابطهي 13)
|
- حالت دوم - .gif)
در اين صورت خواهيم داشت:
(رابطهي 14)
در صورت وجود حالت دوم، سه حالت ديگر ممكن است:
|  .gif) و و .gif)
در اين حالت داريم:
(رابطهي 15)
و همچنين داريم:
(رابطهي 16)
در نتيجه داريم:
(رابطهي 17)
| | | |  .gif) و و .gif)
در اين حالت داريم:
(رابطهي 18)
و همچنين داريم:
(رابطهي 19)
در نتيجه داريم:
(رابطهي 20)
| | | |  .gif) و و .gif)
در اين حالت داريم:
(رابطهي 21)
و همچنين داريم:
(رابطهي 22)
در نتيجه داريم:
(رابطهي 23)
|
| ساير نامساويها در اعداد حقيقي |
«نامساوي در مثلث» (The Triangle Inequality) در اعداد حقيقي را ميتوان در شكلهاي ديگري نيز بيان كرد:
(رابطهي 24)
و يا داريم:
(رابطهي 25)
ميتوانيم رابطههاي ذيل را در مورد «نامساوي در مثلث» (The Triangle Inequality) بنويسيم:
(رابطهي 26)
(رابطهي 27)
(رابطهي 28)
در هر مثلث .gif) با اضلاع با اضلاع .gif) ، ، .gif) و و .gif) بهترتيب روبهروي زواياي بهترتيب روبهروي زواياي 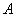 ، ، .gif) و و .gif) ، «محيط» ، «محيط» .gif) و «مساحت» و «مساحت» .gif) از روابطي نظير ذيل بهدست ميآيد: از روابطي نظير ذيل بهدست ميآيد:
(رابطهي 29)
(رابطهي 30)
ميتوان ثابت كرد كه در هر مثلث ميتوان نامساويهاي ذيل را نوشت:
(رابطهي 31)
| - .gif) اگر و فقط اگر اگر و فقط اگر .gif) | | | | - .gif) اگر و فقط اگر اگر و فقط اگر .gif) | | | | - .gif) اگر و فقط اگر اگر و فقط اگر .gif) |
(رابطهي 32)
(رابطهي 33)
(رابطهي 34)
(رابطهي 35)
(رابطهي 36)
(رابطهي 37)
(رابطهي 38)
(رابطهي 39)
(رابطهي 40)
(رابطهي 41)
(رابطهي 42)
(رابطهي 43)
(رابطهي 44)
(رابطهي 45)
رابطهي 45 توسط «سيدونز» (Siddons) و «هوقس» (Hughes) در سال 1308 (1929 ميلادي) اثبات شد.
(رابطهي 46)
| قضيهي هينگه (Hinge Theorem) |
«قضيهي هينگه»(Hinge Theorem) براي مقايسهي دو مثلث بهكار ميرود كه داراي دو ضلع متجانس باشند. مطابق اين قضيه، اگر دو ضلع يك مثلث با دو ضلع مثلث ديگر متجانس باشد و زاويهي بين دو ضلع مثلث اول بزرگتر از مثلث دوم باشد در اين صورت ضلع سوم مثلث اول قطعاً از ضلع سوم مثلث دوم بزرگتر خواهد بود.معكوس «قضيهي هينگه» (Hinge Theorem) نيز صادق است: اگر دو ضلع يك مثلث با دو ضلع مثلث دوم متجانس باشند و ضلع سوم مثلث اول بزرگتر از ضلع سوم مثلث دوم باشد؛ همچنين زاويهي بين دو ضلع متجانس مثلث دوم از زاويهي بين مثلث اول بزرگتر باشد در اين صورت زاويهي روبهروي ضلع سوم مثلث اول بزرگتر خواهد بود زيرا ضلع سوم مثلث اول از ضلع سوم مثلث دوم بزرگتر است.
(رابطهي 47)
| مثالهايي از قضيهي هينگه (Hinge Theorem) |
| مثال اول – سفر با هواپيما |
شما و دوستتان با هواپيماهاي متفاوتي مسافرت ميكنيد. در حالي كه هواپيماي شما در 120 كيلومتري شمال فرودگاه است هواپيماي دوستتان در 120 كيلومتري جنوب فرودگاه قرار گرفته است. در اين لحظه، هواپيماي شما 70 كيلومتر با زاويهي 30 درجه بهسمت شمالشرق پرواز ميكند. در همان حال، هواپيماي دوستتان تغيير مسير داده و 70 كيلومتر با زاويهي 40 درجه بهسمت جنوبغربي حركت ميكند. در حالي كه هر دو هواپيما 190 كيلومتر پيموده باشند كداميك از فرودگاه فاصلهي بيشتري گرفته است؟ بهراحتي با استفاده از «قضيهي هينگه» (Hinge Theorem) ميتوان نتيجه گرفت هواپيماي دوستتان فاصلهي بيشتري از فرودگاه دارد.
(رابطهي 48)
دو مثلث با مشخصات ذيل را در نظر بگيريد: | - يكي از رؤوس هر دو مثلث در مركز يك دايره قرار گرفته است. | | - دو رأس ديگرشان بر روي محيط آن دايره واقع است. |
چنانچه زاويهي مربوط به رأس واقع در مركز دايره در مثلث اول بزرگتر باشد ضلع روبهروي آن زاويه در كدام مثلث كوچكتر خواهد بود؟
همانطور كه در شكل 3 نشان داده شده است مثلث اول .gif) و مثلث دوم و مثلث دوم .gif) است و داريم: است و داريم:
(رابطهي 49)
در نتيجه داريم:
(رابطهي 50)
| يك نامساوي قوي در مثلث (Hinge Theorem) |
در سال 1376 (1997 ميلادي) «هـ. ر. باييلي» (H. R. Bailley) يك مهندس بازنشسته و «ر. بانيستر» (R. Bannister) يك شيميدان بازنشسته نتيجهاي عجيب منتشر كردند كه به «نامساوي قوي در مثلث» (Strengthened Triangle Ineqality) مشهور شد؛ وجه تسميهي ان نيز مربوط به بيشترين كاربرد آن است.كمي بعد پروفسور «موراي كلامكين» (Murray Klamkin) - يكي از افرادي كه اخيراً مسائل زيادي توسط وي حل شده است – اثباتي يكصفحهاي براي آن ارائه داد. «هـ. ر. باييلي» (H. R. Bailley) و «ر. بانيستر» (R. Bannister) براي بيان رابطهي خود از يك مثلث قايمالزاويه و يك مربع محاط بر آن استفاده كردند. آنان دو روشي را كه يك مربع ميتواند در يك مثلث قايمالزاويه محاط شود مقايسه كردند. سؤال اين بود كه كدام مربع بزرگتر است؟ فرض كنيد داشته باشيم:
در هر دو شكل، وجود مثلثهاي مشابه منجر به روابط ذيل ميشود:
(رابطهي 51)
از روابط 21 ميتوان رابطهي ذيل را نتيجه گرفت:
(رابطهي 52)
و سرانجام رابطهي ذيل را ميتوان بهدست آورد:
(رابطهي 53)
بنابراين در يك مثلث قايمالزاويه هم .gif) و هم و هم .gif) هر دو برابر با مساحت مثلث هستند بنابراين داريم: هر دو برابر با مساحت مثلث هستند بنابراين داريم:
(رابطهي 54)
لذا از روابط 50 ميتوان نتيجه گرفت كه نسبت اندازهي مساحتهاي مربعها با اندازههاي .gif) و و .gif) نسبت عكس دارد. نسبت عكس دارد. براي مقايسهي اندازههاي .gif) و و .gif) ، تفاوت مربعهاي آنها را محاسبه ميكنيم: ، تفاوت مربعهاي آنها را محاسبه ميكنيم:
(رابطهي 55)
از رابطهي فوق چنين نتيجه ميگيريم: در يك مثلث قايمالزاويه هميشه رابطهي ذيل صادق است:
(رابطهي 56)
رابطهي 26 بدينمعنا است كه:
(رابطهي 57)
بنابراين اضافه كردن ارتفاع .gif) منجر به معكوس «نامساوي در مثلث« ميشود: منجر به معكوس «نامساوي در مثلث« ميشود:
(رابطهي 58)
طبيعي بود كه «هـ. ر. باييلي» (H. R. Bailley) و «ر. بانيستر» (R. Bannister) پس از اثبات اين مطلب، پيش رفته و مقادير .gif) و و .gif) را براي مثلثهايي غير از قايمالزاويه بررسي كنند. نتايج بهدست آمده توسط آنان هيجانانگيز بود. را براي مثلثهايي غير از قايمالزاويه بررسي كنند. نتايج بهدست آمده توسط آنان هيجانانگيز بود. در يك مثلث با اضلاع .gif) ، ، .gif) و و .gif) ارتفاع ارتفاع .gif) و زاويهي و زاويهي .gif) روبهروي ضلع روبهروي ضلع .gif) باشد در اين صورت خواهيم داشت: باشد در اين صورت خواهيم داشت:
(رابطهي 59)
رابطهي 59 زماني محقق ميشود كه رابطهي ذيل را داشته باشيم:
(رابطهي 60)
يا همانطور كه «هـ. ر. باييلي» (H. R. Bailley) و «ر. بانيستر» (R. Bannister) ابراز داشتهاند رابطهي 59 براي بيشتر مثلثهايي صادق است كه داشته باشيم:
(رابطهي 61)
علاوه بر آن ميدانيم:
(رابطهي 62)
اثبات ذيل به پروفسور «موراي كلامكين» (Murray Klamkin) منتسب شده است كه براساس اتحاد ذيل بيان شده است:
(رابطهي 63)
رابطهي فوق در هر مثلثي صادق است و در آن زواياي 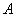 و و .gif) بهترتيب روبهروي اضلاع بهترتيب روبهروي اضلاع .gif) و و .gif) هستند. هستند. براي مقادير ثابت .gif) ، نسبت ، نسبت .gif) زماني حداقل خواهد بود كه زماني حداقل خواهد بود كه 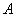 و و .gif) با يكديگر مساوي باشند (مثلث متساويالساقين): با يكديگر مساوي باشند (مثلث متساويالساقين):
(رابطهي 64)
لذا براي مثلث با زواياي حاده رابطهي ذيل را خواهيم داشت:
(رابطهي 65)
رابطهي 65 تنها و تنها زماني صادق است كه داشته باشيم:
(رابطهي 66)
براي اينكه رابطهي 59 برقرار باشد بايد داشته باشيم:
(رابطهي 67)
سمت چپ رابطهي 67 يك تابع نزولي از بوده و برابر با 1 است زماني كه داشته باشيم:
(رابطهي 68)
و زماني رابطهي 68 برقرار است كه داشته باشيم:
(رابطهي 69)
بنابراين رابطهي 59 زماني برقرار است كه نامساوي ذيل صادق باشد:
(رابطهي 70)
بدينترتيب تنها كافي است رابطهي 63 را ثابت كنيم. اگر .gif) شعاع دايرهي محيطي مثلث شعاع دايرهي محيطي مثلث .gif) باشد داريم: باشد داريم:
(رابطهي 71)
بنابراين داريم:
(رابطهي 72)
با استفاده از رابطههاي مقدماتي مثلثاتي و اينكه: .gif) ، رابطهي ذيل بهدست خواهد آمد: ، رابطهي ذيل بهدست خواهد آمد:
(رابطهي 73)
از آنجايي كه در هر مثلث مجموع زواياي داخلي مثلث برابر 180 درجه است داريم:
(رابطهي 74)
با جايگذاري رابطهي 74 در رابطهي 73 خواهيم داشت:
(رابطهي 75)
«موراي كلامكين» (Murray Klamkin) يك رياضيدان امريكايي است كه در 14 اسفند 1300 (1921 ميلادي) در «بروكلين» نيويورك بهدنيا امد. وي در سال 1321 (1942 ميلادي) درجهي «كوپر يونيون» (Cooper Union) (شاگرد اولي) را بهدست آورده و در سال 1326 (1947 ميلادي) بهسمت استادي «انستيتو پليتكنيك بروكلين» (Polytechnic Institute of Brooklyn) نايل آمد؛ در سالهاي 1327 تا 1336 (1948 تا 1957 ميلادي) در آن دانشگاه تدريس ميكرد.وي در سالهاي 1341 تا 1355 (1962 تا 1976 ميلادي) در چند شركت امريكايي نيز اشتغال داشت. در اين سالها، استاد مهمان «دانشگاه مينوستا» (University of Minoseta) نيز بود. در سال 1355 (1976 ميلادي) بهسمت پروفسوري «دانشگاه واترلو» (University of Waterloo) نايل شد. در سالهاي 1315 تا 1360 (1976 تا 1981 ميلادي) رئيس گروه رياضي «دانشگاه آلبرتا» (University of Alberta) بود. در سال 1360 بهسمت «ايمريتوس پروفسور» (پروفسور بازنشسته) (Emeritus Professor) نايل آمد. «موراي كلامكين» (Murray Klamkin) به طراح و ويراستار سؤالهاي رياضي مشهور است. وي ويراستار ماهنامهي امريكايي «سيام رويو» (SIAM Review) و مجلههاي ديگري بوده است. وي همچنين بهخاطر فعاليتهايش در رقابتهاي بينالمللي از جمله: «المپياد ملي ايالات متحدهي امريكا» (United States of America Mathematical Olympiad) (USAMO)، «المپياد جهاني رياضي» (the International Mathematical Olympiad) (IMO) و «رقابتهاي پوتنام» (Putnam Competition) شهرت يافته است. در سال 1371 (1992 ميلادي)، «فدراسيون جهاني رقابتهاي رياضي امريكا» (The World Federation of National Mathematics Competitions)، جايزهي «ديويد هيلبرت» (David Hilbert) را بهخاطر همكاريهايش در رقابتهاي رياضي به وي اهدا كرد. |