مطلبي كه با عنوان زنگ تفريح تقديم ميشود توسط محققان رياضي «ديويد اشپيكل هالتر» (David Spiegelhalter) پروفسور «وينتون» (Winton) از گروه «درك عمومي از ريسك» (The Public Understanding of Risk) دانشگاه كمبريج و «مايك پيرسون» (Mike Pearson) تهيه و تقديم ميشود. اين دو محقق بههمراه گروهي ديگر از محققان در حال آمادهسازي سايتي هستند كه در آن به موضوع: «درك عدم قطعيت» (Understanding Uncertainty) خواهند پرداخت. در اين سايت بنا دارند از «ريسك» (Risk) و «عدم قطعيت» (Uncertainity) سخن بهميان آورند. اين سايت بنا به ادعايشان بهار 1387 (2008 ميلادي) افتتاح خواهد شد.
«جداول ليگ» (League Tables) از جمله مباحث بحثبرانگيز و بهطور قطع استدلالي در عامهي مردم محسوب ميشوند. با استفاده از اين جداول، بهسادگي با وجود چند چيز ميتوان چيزي شبيه به نتيجه بهدست آورد! بهعنوان مثال ميتوان به مواردي نظير ذيل اشاره كرد:
| - تعداد آزمونهاي موفق | | - تعداد عملهاي موفقيتاميز قلب | | - و ... |
عامهي مردم حتي اگر يك «معيار انتخاب» را براي اين موارد بپذيرند هنوز به «شانس» اعتقاد ندارند. مثال ذيل ميتواند نمونهاي از اين امر محسوب شود: همانطور كه در نگاهي مختصر بررسي خواهيم كرد «جدول ليگ» (League Table) در تمام تاريخ قرعهكشيها نشان داده است كه برخي اعداد داراي امتياز بيشتري براي انتخاب شدن هستند. اين در حالي است كه بعضي از اعداد بعد از چندين دفعه قرعهكشي اصلاً انتخاب نميشوند. آيا تقلبي شده يا دست خدا در كار بوده است؟ لزوماً اينگونه نيست؛ در حقيقت قايل شدن به «ارزش از قبل تعيين شده» (Face-Value) در مورد «جدول ليگ» (League Table) كاملاً نادرست است. در اين مورد واقعاً «شانس» در كار است. در اين زنگ تفريح به اين مسأله دقيقتر پرداخته ميشود.
معلمتان از ابتداي سابقهي تدريسش يعني سال 1373 (1994 ميلادي) اين بازي را به بچهها پيشنهاد داده است. حال بياييم اين بازي را بهدقت بررسي ميكنيم: شش توپ بهقيد قرعه از ميان مجموعهاي از 49 توپ داراي شماره انتخاب ميشوند. اگر دانشاموزي بهطور صحيح شش عدد را پيشبيني كند در جايزهي درنظر گرفته شده سهيم ميشود. انيميشن شكل 3 نشان ميدهد چند وقت به چند وقت هر يك از 49 عدد در اولين 1240 مورد قرعهكشي ممكن است انتخاب شوند. | شكل 3 – انتخاب هر يك از 49 عدد
در اولين 1240 مورد قرعهكشي. |
اگر اعداد انتخاب شده در اولين قرعه را از سال 1373 (1994 ميلادي) بررسي كنيم متوجه ميشويم كه بر روي يك عدد تمركز بيشتري وجود داشته است. اگر بر روي كليد «مرتب كردن» كليك كنيد اعداد برحسب «مرتبه» طبقهبندي ميشوند. كليد «اجراي سريع» براي بالا بردن سرعت عمليات اجرايي است. زماني كه انيميشن پايان مييابد آنچه مشاهده ميشود اعداد براساس مرتبهي «فركانس» طبقهبندي شدهاند. دانشاموزي كه عدد 38 را انتخاب كرده برندهي واقعي است! با كليك كردن بر «هيستوگرام» ميتوانيد نموداري ستوني ايجاد ميشود كه براي هر مقدار 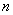 ، تعداد پيشامدهاي واقع شده دقيقاً بهتعداد ، تعداد پيشامدهاي واقع شده دقيقاً بهتعداد 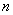 دفعه را نشان ميدهد. كليك كردن بر كليد «بهتصوير كشيدن» (Start Dropping)، نشان ميدهد كه چگونه نمودار ستوني مذكور رسم ميشود. بهنظر ميرسد اين توزيع كه بعضي از اعداد بيش از ديگران ظاهر ميشوند كاملاً شايع باشد. دفعه را نشان ميدهد. كليك كردن بر كليد «بهتصوير كشيدن» (Start Dropping)، نشان ميدهد كه چگونه نمودار ستوني مذكور رسم ميشود. بهنظر ميرسد اين توزيع كه بعضي از اعداد بيش از ديگران ظاهر ميشوند كاملاً شايع باشد. ياداوري – در حالت «اجراي سريع»، كليد «بهتصوير كشيدن» (Start Dropping) دردسترس نيست. ميتوانيم با نگاه بر «شكاف» (Gap) بين هر دفعه كه يك عدد بهطور تصادفي انتخاب ميشود از زاويهي ديگري به اين بحث بپردازيم. انيميشن شكل 4 مسير هر دفعهاي را نشان ميدهد كه يك عدد بهطور تصادفي انتخاب نميشود. | شكل 4 - مسير هر دفعهاي
كه يك عدد بهطور تصادفي انتخاب نميشود. |
اگر بهدقت به شروع سال 1379 (2000 ميلادي) توجه داشته باشيد بيشترين «شكاف» (Gap) مشاهده شده را 72 مييابيد كه براي عدد 17 است. اين عدد در قرعهي 435ام در پنجم اسفند 1379 (23 فوريهي 2000 ميلادي) بهدست آمده است؛ اما دوباره تا قرعهي 508ام در چهاردهم آبان 1379 (چهارم نوامبر 2000 ميلادي) بهقيد قرعه انتخاب نميشود. برگشت به محاسبههاي گذشته نشان ميدهد چنين «شكافي» (Gap) حقيقتاً بهندرت انجام ميشود. شانس وقوع يك عدد بهخصوص در يك تكقرعه برابر .gif) است و بدينمعنا است كه احتمال اينكه يك عدد انتخاب نشود است و بدينمعنا است كه احتمال اينكه يك عدد انتخاب نشود .gif) است. شانس وقوع رويداد 72 دفعه در يك رديف، است. شانس وقوع رويداد 72 دفعه در يك رديف، .gif) است كه تقريباً است كه تقريباً .gif) يا يا .gif) است! است! آنچه «جداول ليگ» (League Tables) تاكنون به ما نشان داده است (عدد خوشبخت 38 و «شكاف» (Gap) از لحاظ اندازه غيرمحتمل) بهنظر نميرسد كه بهخوبي با فرض «صحت تصادفي بودن» تطبيق داشته باشد. اين نقطهاي است كه درك آن مشكل بوده و ممكن است دچار باور وقوع فريب در قرعهكشي شده يا عواملي آسماني را دخيل بدانيم!! اما با كمي تفكر رياضي ميتوان فهميد كه ممكن است بهطور شانسي چنين چيزي اتفاقد بيافتد بنابراين نفس عميقي كشيده و بهاصطلاح مدادتان را تيز كنيد!!
| توزيع تعداد انتخاب شدن هر عدد |
ابتدا نياز داريد يك «توزيع نظري از احتمال» (Theoretical Probability Distribution) را بر اين فرض قرار دهيد كه قرعهي موردنظر تصادفي باشد. فرض كنيد .gif) تعداد گويها در كيف باشد بهگونهاي كه در اين حالت داشته باشيم: تعداد گويها در كيف باشد بهگونهاي كه در اين حالت داشته باشيم:
(رابطهي 1)
(رابطهي 2)
اگر اعداد بهطور تصادفي انتخاب شده باشند براي هر يك، شانس بيرون آمدن از قرعه .gif) بوده و بنابراين در اين حالت داريم: بوده و بنابراين در اين حالت داريم:
(رابطهي 3)
بنابراين شانس يك عدد براي عدم انتخاب در قرعه از رابطهي ذيل بهدست ميآيد:
(رابطهي 4) براي بررسي احتمال اينكه از .gif) قرعه دقيقاً قرعه دقيقاً .gif) دفعه، عددي ويژه بهطور تصادفي انتخاب شود سه عامل را بايد درنظر بگيريم: دفعه، عددي ويژه بهطور تصادفي انتخاب شود سه عامل را بايد درنظر بگيريم: رابطهي 6 «توزيع دوجملهاي» (Binomial Distribution) با متغيرهاي .gif) و و .gif) است. اين توزيع داراي «ميانگين» (Mean) است. اين توزيع داراي «ميانگين» (Mean) .gif) و «واريانس» (Variance) و «واريانس» (Variance) .gif) است. در اينجا به مقادير بزرگ است. در اينجا به مقادير بزرگ .gif) علاقهمند بوده و براي اين مقادير با تطبيق «ميانگين» و «واريانس»، «توزيع نرمال» (Normal Distribution) تقريباً با «توزيع نرمال نظري» (Theoretical Normal Distribution) نزديك است. علاقهمند بوده و براي اين مقادير با تطبيق «ميانگين» و «واريانس»، «توزيع نرمال» (Normal Distribution) تقريباً با «توزيع نرمال نظري» (Theoretical Normal Distribution) نزديك است. در شكل 5 «توزيع واقعي» اعداد قرعهكشي شده با «توزيع نرمال نظري» (Theoretical Normal Distribution) مقايسه شده است. «توزيع واقعي» اعداد قرعهكشي شده با رنگ «سفيد» و «توزيع نرمال نظري» با رنگ «خاكستري» نشان داده شده است. «توزيع واقعي» ناهموار ديده ميشود ولي «توزيع نظري» به ما اجازه ميدهد بررسي كنيم كه آيا عددي كه اولين دفعه قرعهكشي ميشود در حقيقت بهطور اعجابانگيزي دور است. | شكل 5 – مقايسهي توزيع واقعي» اعداد
قرعهكشي شده با «توزيع نرمال نظري». |
در شكل 6 نمودار «توزيع نهايي» مشاهده شده را با نمودار «توزيع نظري» روي هم ميبينيم. هماندازه بودن خوب بهنظر ميرسد و بيانگر اين است كه اولويت خاصي براي اعداد بهخصوص وجود ندارد. عدد خوشبخت 38 مصداق تقلب نيست. .gif)
| شكل 6 – توزيع «نظري» (Theoretical)
و «مشاهده شده» (Observed). |
| توزيع «شكاف» (Gap) بين انتخاب تصادفي اعداد |
ميتوانيم «توزيع نظري» «شكافها» (Gaps) بين اعداد را به روشي مشابه ايجاد كنيم. عدد بهخصوصي نظير .gif) را درنظر بگيريد. قرعهاي را «موفق» بناميد كه عدد را درنظر بگيريد. قرعهاي را «موفق» بناميد كه عدد .gif) انتخاب شود و در غير اينصورت «شكست» نامگذاري كنيد. همانند قبل، شانس «موفقيت» انتخاب شود و در غير اينصورت «شكست» نامگذاري كنيد. همانند قبل، شانس «موفقيت» .gif) خواهد بود. خواهد بود.
فرض كنيد .gif) تعداد «شكستها» قبل از اولين «موفقيت» باشد بهعبارت ديگر «شكاف» (Gap) قبل از تعداد «شكستها» قبل از اولين «موفقيت» باشد بهعبارت ديگر «شكاف» (Gap) قبل از .gif) دوباره بهطور تصاوفي انتخاب شود. شانس دوباره بهطور تصاوفي انتخاب شود. شانس .gif) براي انتخاب تصادفي عدد بهخصوص براي انتخاب تصادفي عدد بهخصوص .gif) همانند شانس مشاهدهي سرياي از همانند شانس مشاهدهي سرياي از .gif) «شكست» بعد از يك «موفقيت» است؛ بنابراين داريم: «شكست» بعد از يك «موفقيت» است؛ بنابراين داريم:
(رابطهي 7)
اين همان «توزيع هندسي» (Geometric Distribution) است. به اين معنا كه از رابطهي ذيل بهدست ميآيد:
(رابطهي 8)
بنابراين «طول شكاف ميانگين» (Mean Gap Length) حدود 7 است. ياداوري – «توزيع» (Distribution) گاهي اوقات بدينصورت تعريف ميشود: «زمان تا اولين موفقيت» كه در اينجا به .gif) بستگي دارد. بستگي دارد. «هيستوگرام» در شكل 7 توزيع همهي شكافها را با «توزيع هندسي نظري فراتر» (The Theoretical Geometric Distribution Superimposed) نشان ميدهد. شكافها در پايين و بالاي 40 بهگونهاي تقسيم شدهاند كه شكافهاي بزرگ بهطور واضح نشان داده شوند. بهنظر ميرسد «توزيع نظري» بر «توزيع مشاهده شده» تطبيق دارد اگرچه بهضرورت، ناهمواريهاي كوچكي در دنباله وجود دارد. .gif)
| شكل 7 – توزيع «نظري» و
«مشاهده شدهي» شكافها. |
| حداكثر شكافها در تاريخ قرعهكشيها |
اما دربارهي حداكثر شكاف 72 چه نظري داريد كه بهنظر غيرمحتمل ميآيد؟ در نتيجه كمي غلط بهنظر ميرسد كه پرسيده شود: «عدد 17 از قرعه بيرون آمده است؛ شانس اينكه اين عدد در 72 قرعهي بعدي بيرون نيايد چقدر است؟» در حقيقت، نتايج 1240 قرعه را بيش از ظاهر شدن تنها عدد 72 انتظار ميكشيم بهويژه مايل به ظاهر شدن عدد 17 نيستيم.
آنچه بايد پرسيده شود آن است كه: «بعد از 1240 قرعه، شانس اينكه هر يك از شكافها بين دو قرعه از همان عدد بزرگتر از 72 باشد چقدر است؟» براي اين منظور ابتدا نياز داريم بدانيم كلاً چه تعداد شكاف موجود است. 1240 قرعه وجود داشته است كه هر كدام بيانگر 6 عدد هستند؛ بنابراين در مجموع .gif) عدد قرعه كشيده شده است. هربار يك عدد ظاهر ميشود شكافي متناسب با بعد از آن مشاهده ميشود كه شامل شكاف اوليه است تا اينكه هر عدد براي اولين بار بهقيد قرعه ظاهر شود. عدد قرعه كشيده شده است. هربار يك عدد ظاهر ميشود شكافي متناسب با بعد از آن مشاهده ميشود كه شامل شكاف اوليه است تا اينكه هر عدد براي اولين بار بهقيد قرعه ظاهر شود. اكنون سؤال ذيل مطرح ميشود: «شانس اينكه بزرگترين 2440 شكاف حداقل 72 باشد چقدر است؟» ميتوانيم اين شانس را با استفاده از توزيعمان حدس بزنيم:
(رابطهي 9)
كه در آن داريم: | .gif) = شانس اينكه حداكثر شكاف حداقل 72 باشد = شانس اينكه حداكثر شكاف حداقل 72 باشد | | .gif) = شانس اينكه حداكثر شكاف كوچكتر از 72 باشد = شانس اينكه حداكثر شكاف كوچكتر از 72 باشد | | .gif) = شانس اينكه همهي شكافها كوچكتر از 72 باشد = شانس اينكه همهي شكافها كوچكتر از 72 باشد | | .gif) = شانس اينكه = شانس اينكه .gif) كوچكتر از 72 باشد. كوچكتر از 72 باشد. |
بخش پاياني رابطهي 9 بدينعلت برقرار است كه احتمال اينكه همهي شكافها كمتر از 72 بوده تقريباً با حاصلضرب 7440 احتمال معادل برابر باشد كمتر از 72 است. ياداوري – نتيجه تنها تقريبي است بهخاطر اينكه وابستگي اندكي بين شكافها در رابطه با اين امر وجود دارد كه هميشه 6 عدد در هر قرعه موجود باشد. بعداً چگونگي خوب بودن چنين تقريبي را بررسي خواهيم كرد. بنابراين رابطهي ذيل صادق خواهد بود:
(رابطهي 10)
نتيجه نشان ميدهد كه يك شكاف حداكثر با طول 72 بههيچ وجه غيرمنتظره نخواهد بود. در حقيقت، شانس 50 – 50 مربوط به شكاف با حداقل طول در 1240 قرعه خواهد بود. براي بررسي صحت اين نتيجه ميتوانيم از شبيهسازي «ساختگي» (Fictional) تاريخچهي قرعهكشي بر روي يك كامپيوتر استفاده كنيم. بدينترتيب كه 6 عدد متفاوت را بهصورت تصادفي از 1 تا 49 انتخاب كنيم؛ سپس اين فرايند را 1240 بار تكرار مينماييم. نرمافزاري كه استفاده ميكنيم شامل توليدكنندههاي اعداد تصادفي باشد كه بايد ما را متقاعد كند كه هر عدد حقيقتاً داراي شانس مساوي براي انتخاب شدن است. بدينترتيب 1000 مورد تاريخي از قرعهكشي شبيهسازي شده و متوجه ميشويم كه بزرگترين شكاف در هر مورد شامل 470 مورد (47 درصد) خارج از 1000، 72 يا بيشتر است (شكل 8) كه به احتمال نظري تقريبي ما يعني 46/0 (رابطهي 10) شبيه است و نشاندهندهي درستي رابطهي 10 است. .gif)
| شكل 8 – حداكثر شكاف مشاهده شده
بين همان عدد كه در 1240 قرعه ظاهر شده است. |
| آزمودن عدم بيطرفي در انتخاب قرعه |
تناسب خوب بين توزيعهاي «نظري» و «مشاهده شده» بيانگر آن است كه آنچه در 1240 قرعه مشاهده ميكنيم با اين فرض تطبيق دارد كه «قرعهكشي» تصادفي است. با اين حال، اين توزيعها با يكديگر تفاوت دارند. قبل از اينكه نگران باشيم بايد ببينيم چقدر ميتوانيم به اين تفاوت دامن بزنيم. بهعبارت ديگر، چه اطميناني وجود دارد كه نتيجهي بهدست آمده از «قرعهكشي» تصادفي باشد؟ «نظريهي احتمال» (Probability Theory) به اين سؤال جواب ميدهد. در حقيقت، آزمونهاي آماري بسياري براي تعيين راههاي مختلف وجود دارد كه بهواسطهي آن «قرعه» ممكن است كاملاً تصادفي نباشد. بياييد يكي از اين راههاي ساده را با هم بررسي كنيم.
«توزيع دوجملهاي» (Binomial Distribution) بالا ميگويد انتظار داريم بعد از .gif) قرعه هر عدد ويژهاي با تعداد دفعههاي ذيل ظاهر شود: قرعه هر عدد ويژهاي با تعداد دفعههاي ذيل ظاهر شود:
(رابطهي 11)
در اين مثال، قرعهكشي توسط معلم به.gif) يا تقريباً يا تقريباً .gif) بستگي دارد. بنابراين براي مثال بعد از 1240 قرعه انتظار خواهيم داشت هر عدد انتخاب شده حدود بستگي دارد. بنابراين براي مثال بعد از 1240 قرعه انتظار خواهيم داشت هر عدد انتخاب شده حدود.gif) دفعه ظاهر شود. اكنون تعداد كل دفعههايي كه هر عدد بعد از دفعه ظاهر شود. اكنون تعداد كل دفعههايي كه هر عدد بعد از .gif) قرعه ظاهر ميشود را به آن بيافزاييد؛ سپس آن را قرعه ظاهر ميشود را به آن بيافزاييد؛ سپس آن را .gif) ، ، .gif) و ... بناميد تا اينكه به و ... بناميد تا اينكه به .gif) برسيد. برسيد. براي هر عدد .gif) ، عبارت ذيل معياري است براي «عدم همخواني» (Discrepancy) بين آنچه مشاهده ميشود و آنچه انتظار داريم: ، عبارت ذيل معياري است براي «عدم همخواني» (Discrepancy) بين آنچه مشاهده ميشود و آنچه انتظار داريم:
(رابطهي 12)
اگر مقادير .gif) را براي 49 مقدار را براي 49 مقدار .gif) جمع ببنديم معياري كلي براي «عدم همخواني» (Discrepancy) بهدست خواهد آمد. نتيجهي بهدست آمده اصطلاحاً «آمار چي دو» (Chi Squared Statics) ناميده و با جمع ببنديم معياري كلي براي «عدم همخواني» (Discrepancy) بهدست خواهد آمد. نتيجهي بهدست آمده اصطلاحاً «آمار چي دو» (Chi Squared Statics) ناميده و با .gif) نشان داده ميشود. براي همانندسازي لازم است «آمار چي دو استاندارد» (Standard Chi Squared Statics) را در مقدار نشان داده ميشود. براي همانندسازي لازم است «آمار چي دو استاندارد» (Standard Chi Squared Statics) را در مقدار .gif) ضرب كنيم. علت آن است كه همانطور كه قبلاً ذكر شد مقادير كلي كاملاً مستقل نيستند. اين شگردها در «نظريهي آمار» (Statistical Theory) انجام ميشود كه قصد نداريم وارد اين مبحث شويم. ضرب كنيم. علت آن است كه همانطور كه قبلاً ذكر شد مقادير كلي كاملاً مستقل نيستند. اين شگردها در «نظريهي آمار» (Statistical Theory) انجام ميشود كه قصد نداريم وارد اين مبحث شويم. تنها بهعنوان اينكه حداكثر استفاده را از «توزيع نظري» (Theoretical Distribution) در وقوع هر تعدادي كرده باشيم بسته به اين فرض كه «قرعهكشي» تصادفي است ممكن است نهايتاً به توزيع .gif) نياز داشته باشيم كه به آن اصطلاحاً يك «توزيع چي دو استاندارد» (Standard Chi Squared Distribution) در وضعيت نياز داشته باشيم كه به آن اصطلاحاً يك «توزيع چي دو استاندارد» (Standard Chi Squared Distribution) در وضعيت .gif) «درجهي آزادي» (Degree of Freedom) اطلاق ميشود. «درجهي آزادي» (Degree of Freedom) اطلاق ميشود. اين به ما ميگويد كه شانس ظاهر شدن عدد مورد نظرمان براي .gif) - با اين فرض كه قرعهكشي واقعاً تصادفي است يعني همهي توپهايي كه بهقيد قرعه انتخاب ميشوند از لحاظ آماري مستقل هستند - «كم» است مثلاً: 05/0 يا 5 درصد. به اين دليل بايد نگران انتخاب اعداد مورد نظرمان باشيم!! - با اين فرض كه قرعهكشي واقعاً تصادفي است يعني همهي توپهايي كه بهقيد قرعه انتخاب ميشوند از لحاظ آماري مستقل هستند - «كم» است مثلاً: 05/0 يا 5 درصد. به اين دليل بايد نگران انتخاب اعداد مورد نظرمان باشيم!! دربارهي خود «توزيع چي دو» (Chi Squared Distribution) بيش از اين صحبت نميكنيم. تمام چيزي كه ميگوييم آن است كه وضعيت مورد نظر به ما ميگويد مقدار مشاهده شدهي بايد جايي در اطراف 48 باشد. همچنين به ما ميگويد شانس ظاهر شدن عدد مورد نظرمان بيش از 69 يا كمتر از 9/38 باشد تنها 05/0 يا 5 درصد است. بنابراين بايد مراقب اعداد ظاهر شده در آن محدوده باشيم. «هيستوگرام» شكل 9 اعداد ظاهر شده از آمار را نشان ميدهد كه در آن، قرعهها در گروههاي پنجاهتايي جمع شده و بنابراين در هر حالت رابطهي ذيل برقرار است:
(رابطهي 13) در حالي كه عمليات قرعهكشي به سرانجام ميرسد همهي مقادير مشاهده شده (ظاهر شده) بين خطوط نقطهچين در فواصل 60 و 9/38 قرار ميگيرد. بدينترتيب است كه انصافاً بايد مطمئن شويم كه «قرعهكشي» حقيقتاً «عملياتي تصادفي» است. .gif)
| شكل 9. |
|