ویژگی بازتاب، یکی از ویژگی‌های مهم و برجسته‌ی بیضی است. از آن‌جا که اثبات‌ این ویژگی، از طریق حساب دیفرانسیل و انتگرال اغلب کسل‌کننده است، بنابراین، ما در اینجا، اثبات بسیار کوتاه و زیبایی با استفاده از مشتق می‌آوریم. اثبات ما به طور تعجب‌آوری ساده و کاملا با استفاده از فرمول

 EP = a - ex است.

‌

فرمول EP = a - ex (رابطه‌ی 1) برای فاصله هر نقطه P به مختصات (x, y) روی بیضی از کانون F در جهت مثبت محور xها استوار است. رابطه‌ی (1) را به آسانی می‌توان از رابطه‌های شناخته شده در بیضی، یعنی: x²/a² + y²/b² =1، a²=b²+c² و c/a=e به دست آورد. برای این کار خواهیم داشت:

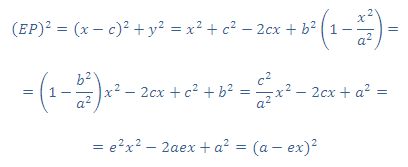
‌با توجه به اینکه در بیضی x≤a و  e<1 برقرار است، بنابراین معادله‌ی 1 به‌دست می‌آید. با تعویض علامت C، با روش مشابه بالا، خواهیم داشت:

رابطه‌ی (۲)            F'P = a + ex 

ما همچنین، می‌توانستیم فرمول (2) را از فرمول (1) با توجه به تعریف بیضی، یعنی PF+PF'=2a به دست بیاوریم. و توجه داریم، که از ویژگی معلوم محور کانونی بیضی، FP/PD=e، رابطه (1) خیلی ساده‌تر به روش زیر قابل اثبات است: می‌دانیم که چون:

 a-c)/(d-a) = e)  که d=a/e،

بنابراین: FP=e.PD=e(d-x)=a-ex ، و به روش مشابه، F'P=a+ex.

‌و برعکس، از رابطه‌ی 1، ویژگی محور کانونی را می‌توان به دست آورد.

‌در حقیقت، قرار بدهیم، d=a/e، FP=a-ex=ed-ex=e.PD.

‌فرض می‌کنیم، (x₀,y₀) نقطه‌ی ثابتی بر بیضی، و (x, y) نقطه‌ی متغیری بر خط مماس بر بیضی باشد، حال به ویژگی بازتاب بر می‌گردیم:

‌
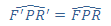
مختصات نقطه P را به صورت (x₀,y₀) نشان می‌دهیم، معادله‌ی خط مماس بر بیضی در نقطه‌ی P به صورت زیر است:

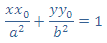
‌که باتوجه به شکل، مختصات نقطه‌ی R به صورت (a²/x₀ ,0) است. حالا با استفاده از رابطه‌های 1 و 2 محاسبه می کنیم:

‌

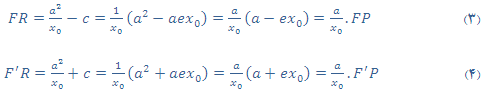
با توجه به قانون سینوس‌ها، در مثلث FRP و استفاده از رابطه‌ی (3) خواهیم داشت:

‌
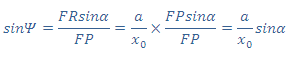
و به روش مشابه، با استفاده از رابطه‌ی (4) و قانون سینوس‌ها برای مثلث F'RP  نتیجه می‌گردد:

‌
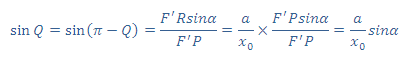
بنابراین sinQ = sinΨ، و با توجه به 0≤Q+Ψ<π  نتیجه می‌گردد Q=Ψ است.

غلامرضا پورقلی