آيا تاكنون با اين مسأله برخورد كرده‌ايد كه صفحه را مي‌توان با چه مجموعه‌هايي پوشاند؟ منظور ما از پوشاندن اين است كه مجموعه‌اي مساوي باشد با اجتماع مجموعه‌هايي ديگر، به‌طوري كه آن مجموعه‌ها هيچ اشتراكي با هم نداشته باشند. مثلاً صفحه را مي‌توان با «بي‌نهايت خط راست» پوشاند به‌طوري كه اين خطوط همديگر را در هيچ نقطه‌اي قطع نكنند.
ولي چندين سال پيش رياضي‌دانان اثبات كردند كه اين كار با استفاده از «دايره‌هاي مجزا» ممكن نيست يعني صفحه را نمي‌توان با دايره‌هاي مجزا به‌طور كامل پوشاند.
در يك سمينار مسأله - كه در «مؤسسه‌ي سلطنتي تكنولوژي استكهلم» برگزار شد - «پروفسور شاپيرو» (H. S. Shapiro) خواستار ارائه‌ي راه‌حلي براي مسأله‌ي پوشانيدن «فضاي اقليدسي سه بعدي» R³ با «خم‌هاي ژوردان» مجزا شد (مي‌توان نشان داد كه فضاي اقليدسي دو بُعدي R² را نمي‌توان با اين روش پوشانيد).




‌در اين يادداشت، ما خانواده‌اي از دايره‌هاي مجزا مي‌سازيم كه اجتماع آن‌ها R³ باشد. منظورمان از دايره مجموعه‌ي ذيل است: 

كه در آن r يك عدد حقيقي مثبت است.
  
فرض كنيد r يك عدد حقيقي نامنفي است و

در اين صورت:

فرض كنيد C اجتماع دايره‌هاي ذيل باشد: 

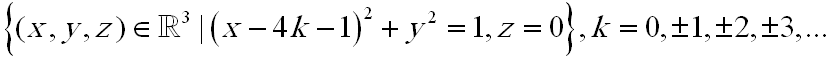
به آساني مي‌توان تحقيق كرد كه براي هر r مثبت، اشتراك C با S_r از دو نقطه تشكيل شده است (به شكل بالا دقت كنيد).
بنابراين:

كه در آن:

اكنون مي‌توان از هر Tr يك «دايره‌ي عظيمه‌ي» Cr را حذف كرد به‌طوري كه  Tr - Cr=T'r U T"r   ، كه در آن T'r و T"r نيم‌كره‌هايي بازند منتها با يك نقطه كم‌تر.
بنابراين كافي است هر T'r و T"r را با دايره‌هاي مجزا بپوشانيم. اين پوشش را مي‌توان مثلا با تقاطع هر T'r و T"r با يك خانواده از صفحه‌ها - آن‌گونه كه در شكل ذيل نشان داده شده است -‌ به‌دست آورد.

منابع:
1. جنگ رياضي دانشجو، جلد هفتم، بهمن 1370،‌ صفحه 140 تا 141.