فرض كنيد .gif) بزرگترين مقسومعليه مشتركي باشد كه بهدنبال يافتن آن هستيم. نشان خواهيم داد كه: بزرگترين مقسومعليه مشتركي باشد كه بهدنبال يافتن آن هستيم. نشان خواهيم داد كه:
(رابطهي 1)
|  مرحلهي اول – بزرگترين مقسومعليه مشترك مرحلهي اول – بزرگترين مقسومعليه مشترك .gif) بر بر .gif) بخشپذير است. بخشپذير است.
براي اثبات از «فرمول چندجملهاي» استفاده ميكنيم:
(رابطهي 2)
(رابطهي 3)
با كم كردن رابطهي 3 از رابطهي 2 خواهيم داشت:
(رابطهي 4)
بنابراين بزرگترين مقسومعليه مشترك .gif) از از 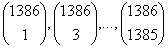 بايد بر بايد بر .gif) جمع آنها يعني بخشپذير باشد. همانطور كه فرض شده بود. جمع آنها يعني بخشپذير باشد. همانطور كه فرض شده بود. | |  مرحلهي دوم – چون بزرگترين مقسومعليه مشترك مرحلهي دوم – چون بزرگترين مقسومعليه مشترك .gif) بايد بر بايد بر .gif) بخشپذير باشد اثبات ميكنيم كه بخشپذير باشد اثبات ميكنيم كه .gif) يا 1 است يا 2. يا 1 است يا 2.
| |  مرحلهي سوم – مرحلهي سوم – .gif) براي براي .gif) «زوج» است. «زوج» است.
براي اثبات از اتحاد ذيل استفاده ميكنيم:
(رابطهي 5)
در اين صورت خواهيم داشت:
(رابطهي 6)
از آنجايي كه سمت راست رابطهي 6 عددي «صحيح» و «زوج» است و اين در حالي است كه .gif) هميشه «فرد» است نتيجه ميگيريم كه هميشه «فرد» است نتيجه ميگيريم كه .gif) بايد «زوج» باشد. بنابراين همهي ضرايب چندجملهاي ما «زوج» خواهد بود. بايد «زوج» باشد. بنابراين همهي ضرايب چندجملهاي ما «زوج» خواهد بود. در نتيجه چون بزرگترين مقسومعليه مشترك .gif) برابر 2 خواهد بود همانطور كه ادعا كرده بوديم. برابر 2 خواهد بود همانطور كه ادعا كرده بوديم.
|
در مرحلهي 3 از روابطي استفاده كرديم كه بهوسيلهي يك اتحاد آشنا بهدست آوردهايم:
(رابطهي 7)
يا اينكه ميتوانيم از «استدلال كميتهاي» استفاده كنيم: براي انتخاب كميتهاي .gif) عضوي با يك رئيس ميتوانيم يكي از عضوي با يك رئيس ميتوانيم يكي از .gif) عضو را (با يكي از عضو را (با يكي از .gif) روش) برگزينيم و سپس رئيس را از ميان آنها انتخاب كنيم يا اينكه ميتوانيم رئيس را از تمام اعضاي گروه ( روش) برگزينيم و سپس رئيس را از ميان آنها انتخاب كنيم يا اينكه ميتوانيم رئيس را از تمام اعضاي گروه (.gif) نفر) برگزينيم و سپس نفر) برگزينيم و سپس .gif) عضو آن گروه را از عضو آن گروه را از .gif) عضو آن گروه انتخاب نماييم. عضو آن گروه انتخاب نماييم. بهجاي راهحل مرحلهي اول ميتوان از راه ديگري نيز استفاده كرد. از آنجايي كه داريم:
(رابطهي 7)
اين رابطه نشان ميدهد كه .gif) ، ، .gif) و و .gif) بهترتيب بر 7، 9 و 11 بخشپذير نيستند. بهترتيب بر 7، 9 و 11 بخشپذير نيستند. نتيجههايي كليتر از اين استدلال ميتوان بهدست آورد:
|