ثابت كنيد براي هر عدد صحيح .gif) ، عبارت ذيل عددي زوج است:
، عبارت ذيل عددي زوج است:
از «قضيهي ويلسون» كمك بگيريد.
براي .gif) عبارت
عبارت .gif) برابر صفر خواهد بود كه عددي زوج است:
برابر صفر خواهد بود كه عددي زوج است:
(رابطهي 1)
اكنون براي مقادير .gif) عبارت مذكور را بررسي ميكنيم.
عبارت مذكور را بررسي ميكنيم.
اعداد صحيح .gif) و
و .gif) ممكن است دو حالت داشته باشد:
ممكن است دو حالت داشته باشد:
| الف - عدد صحيح غير اول |
| ب – عدد صحيح اول |
الف – .gif) و
و .gif) عدد صحيح غير اول
عدد صحيح غير اول
 اگر
اگر .gif) و
و .gif) عدد صحيح غير اول باشند طبق «نظريهي ويلسون» بايد بر
عدد صحيح غير اول باشند طبق «نظريهي ويلسون» بايد بر .gif) بخشپذير باشند. همچنين اعداد
بخشپذير باشند. همچنين اعداد .gif) و
و .gif) نسبت به هم اول هستند لذا مضربهاي آنها نيز بر
نسبت به هم اول هستند لذا مضربهاي آنها نيز بر .gif) بخشپذيراند.
بخشپذيراند.
ياداوري - يكي از .gif) و
و .gif) ميتواند زوج باشد (همزمان نميتوانند زوج باشند)
ميتواند زوج باشد (همزمان نميتوانند زوج باشند)
با فرض .gif) ، عبارت بر 2 بهتوان بيش از بخشپذير است بنابراين عبارت زوج خواهد بود.
، عبارت بر 2 بهتوان بيش از بخشپذير است بنابراين عبارت زوج خواهد بود.
ب - .gif) و
و .gif) عدد صحيح اول
عدد صحيح اول
 اگر
اگر .gif) عدد صحيح اول باشد:
عدد صحيح اول باشد:
در اين صورت .gif) عددي غير اول بوده لذا بر
عددي غير اول بوده لذا بر .gif) بخشپذير است. عددي مانند
بخشپذير است. عددي مانند .gif) را بهصورت ذيل تعريف ميكنيم:
را بهصورت ذيل تعريف ميكنيم:
با بهكار بردن «نظريهي ويلسون» باقيماندهي تقسيم .gif) بر
بر .gif) عدد يك خواهد بود:
عدد يك خواهد بود:
در نتيجه باقيماندهي تقسيم .gif) بر
بر .gif) نيز همان عدد يك خواهد بود:
نيز همان عدد يك خواهد بود:
بنابراين تقسيم .gif) بر
بر .gif) باقيماندهي
باقيماندهي .gif) دارد:
دارد:
از اين مسأله نتيجه ميگيريم كه .gif) عددي صحيح خواهد بود.
عددي صحيح خواهد بود.
اما از آنجايي كه .gif) زوج است
زوج است .gif) فرد بوده بنابراين
فرد بوده بنابراين .gif) نيز فرد است.
نيز فرد است.
ميدانيم:
از طرفي داريم:
بنابراين عبارت فوق نيز عددي زوج خواهد بود.
 اگر
اگر .gif) عدد صحيح اول باشد:
عدد صحيح اول باشد:آنگاه .gif) عددي صحيح و زوج است بنابراين
عددي صحيح و زوج است بنابراين .gif) عددي صحيح و فرد خواهد بود. با استفاده از «نظريهي ويلسون» باقيماندهي تقسيم
عددي صحيح و فرد خواهد بود. با استفاده از «نظريهي ويلسون» باقيماندهي تقسيم .gif) بر
بر .gif) عدد
عدد .gif) بوده و لذا
بوده و لذا .gif) عددي صحيح و فرد خواهد بود:
عددي صحيح و فرد خواهد بود:
بنابراين عبارت ذيل عددي زوج است:
ياداوري – «نظريهي ويلسون» (Wilson's Theorem) كه بيان ميدارد .gif) عددي اول است اگر باقيماندهي تقسيم
عددي اول است اگر باقيماندهي تقسيم .gif) بر
بر .gif) عدد
عدد .gif) باشد
باشد .gif) .
.
اگر .gif) عددي غير اول باشد داراي ضريبي خواهد بود كه كوچكتر و مساوي
عددي غير اول باشد داراي ضريبي خواهد بود كه كوچكتر و مساوي .gif) بوده و بر
بوده و بر .gif) بخشپذير است و لذا بر
بخشپذير است و لذا بر .gif) غيرقابل تقسيم ميباشد. بنابراين باقيماندهي تقسيم
غيرقابل تقسيم ميباشد. بنابراين باقيماندهي تقسيم .gif) بر
بر .gif) عدد
عدد .gif) نخواهد بود:
نخواهد بود:
اكنون فرض كنيد .gif) عدد اول است. اگر
عدد اول است. اگر .gif) باشد در اينصورت باقيماندهي تقسيم
باشد در اينصورت باقيماندهي تقسيم .gif) بر 2 عدد
بر 2 عدد .gif) خواهد بود:
خواهد بود:
اكنون فرض كنيد .gif) فرد است. توجه داشته باشيد اگر باقيماندهي تقسيم
فرد است. توجه داشته باشيد اگر باقيماندهي تقسيم .gif) بر
بر .gif) عدد يك
عدد يك .gif) و
و .gif) باشد در اين صورت داريم:
باشد در اين صورت داريم:
.gif) يا
يا .gif)
براي تقسيم .gif) بر
بر .gif) و بنابراين تقسيم
و بنابراين تقسيم .gif) بر
بر .gif) نتيجه ميدهد:
نتيجه ميدهد: .gif) يا اينكه با تقسيم
يا اينكه با تقسيم .gif) بر
بر .gif) نتيجه ميدهد:
نتيجه ميدهد: .gif) .
.
اكنون براي هر .gif) ، تنها يك
، تنها يك .gif) وجود دارد بهگونهاي كه باقيماندهي تقسيم
وجود دارد بهگونهاي كه باقيماندهي تقسيم .gif) بر عدد
بر عدد .gif) يك باشد
يك باشد .gif) .
.
ما تنها نشان دادهايم كه .gif) است اگر
است اگر .gif) يا
يا .gif) . بنابراين ميتوانيم با تقسيم حاصلضرب هر دو
. بنابراين ميتوانيم با تقسيم حاصلضرب هر دو.gif) بر
بر .gif) عدد يك بهدست آوريم.
عدد يك بهدست آوريم.
ميدانيم حاصلضرب توانهاي 2 شامل: .gif) عبارت است از:
عبارت است از: .gif) .
.
اگر داشته باشيم: .gif) بنابراين
بنابراين .gif) بر
بر .gif) بخشپذير است. بنابراين بهعنوان مثال براي
بخشپذير است. بنابراين بهعنوان مثال براي .gif) عبارت ذيل زوج است:
عبارت ذيل زوج است:
براي .gif) عبارت
عبارت .gif) بر
بر .gif) بخشپذير بوده و
بخشپذير بوده و .gif) بر 8 بخشپذير نيست بهگونهاي كه عبارت ذيل زوج است:
بر 8 بخشپذير نيست بهگونهاي كه عبارت ذيل زوج است:
نهايتاً ميتوانيم در مورد 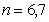 اين موضوع را بهسادگي بررسي كنيم.
اين موضوع را بهسادگي بررسي كنيم.