زنگ تفريح شماره 96

اولین نتیجههای بدست آمده در مورد رنگ امیزی گراف از تلاشهای انجام شده بر روی گرافهای مسطح برای حل مساله رنگ امیزی نقشه بدست آمد. در آن زمان Francis Guthrie ادعا کرد که رنگ امیزی نقشه ایالتهای مختلف بریتانیا روی نقشه، به طوری که هیچ دو ایالت مجاوری همرنگ نشوند، میتواند با ۴ رنگ انجام شود(شرط کافی). برادر Guthrie این مساله را برای معلم ریاضی خود Augustus de Morgan، در University College فرستاد. de Morgan، این مساله را در سال ۱۸۲۵ میلادی در نامهای که به William Hamilton نوشت مطرح کرد. در سال ۱۸۷۹ Arthur Cayley این مساله را در انجمن ریاضی شهر London مطرح کرد. در همان سال Alfred Kempe، نتایج بدست آمده را منتشر کرد و برای یک دهه تصور میشد این مساله حلشدهاست. برای تلاشهای Kempe در این زمینه او به عنوان یکی از اعضای جامعه سلطتنتی و بعدها به عنوان ریاست انجمن ریاضی شهر London انتخاب شد.
در سال Heawood، ادعا کرد که استدلال Kempe اشتباه بودهاست و اثبات این مساله را برای ۵ رنگ منتشر کرد. در قرن معاصر او تلاشهای زیادی برای اثبات روشهای رنگامیزی نقشه با تعداد ۴ رنگ صورت گرفت که در نهایت در سال ۱۹۷۶ توسط Kenneth Appel وWolfgang Haken این مساله به کمک ایدههای خود Heawood و Kempe انجام شد که در آن زمان به دلیل استفاده از کامپیوتر برای اثبات مساله، شدیدا مورد قبول واقع نشد.
رنگ امیزی گراف از اوایل دهه ۷۰ به عنوان یک مساله الگوریتمی مورد بررسی قرار گرفتهاست.
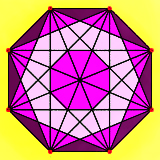
در نظریه گراف، رنگآمیزی کامل گراف یک نوع از رنگآمیزی یالها و راسهای گراف میباشد. اگر این نوع از رنگ آمیزی بدون هیچ شرط و قیدی بیان شود معمولاً اینگونهاست که هیچ راسی، هیچ یال متلاقی و همچنین هیچ یال و رئوس دو سر آن یک رنگ نباشند.
عدد رنگی کامل (χ(G یک گراف حداقل تعداد رنگهای لازم برای رنگ آمیزی کامل یک گراف G است. گراف کامل T = T(G) گراف G یک گراف است با این شرایط : اولاً اینکه مجموعهٔ رئوس T متناظر باشند با رئوس و یالهای G و دوماً اینکه دو راس در T مجاورند اگر و فقط اگر عناصر متناظر آنها در G یا مجاور باشند و یا متلاقی.
رنگ آمیزی یالیk : رنگ امیزی یالی ϐاز گراف بدون طوقه G تخصیص k رنگ 3,2,1,...k به یالهای G است.
رنگ امیزی سره: رنگ امیزی ϐ سره است اگر هیچ دو یال مجاور همرنگ نباشند.
متقابلا K-رنگ امیزی یالی را می توان به صورت یک افراز (E1,E2,...,Ek) از E تصور کرد، که در ان Ei زیرمجموعه ای ( احتمالا خالی ) از E را نشان می دهد که رنگ i را اختیار کرده است. پس k-رنگ امیزی یالی سره، k-رنگ امیزی یالی ( E1, E2, ...,Ek) است که در ان هر زیرمجموعه ی Ei یک جورسازی است.
اگر بخواهيم در يك گراف همه گرهها را به گونهاي رنگ آميزي كنيم كه هيچ دو گره مجاوري يك رنگ نباشند، اين طور عمل ميكنيم كه پيدا كردن حداقل رنگ براي گراف اين چنيني ميباشد اما اين مساله جز يكي از مسايل سمبليك دنياي كامپيوتر ميباشد. از طرفي ميتوان به اين مساله از بعدي ديگر نگريست و آن اين است كه يك گراف مانند G را آيا ميتوان با k رنگ، رنگ آميزي كرد؟
يك رنگ آميزي از گراف G=(V,E) عبارت است از تابعي از رأس هاي گراف به مجموعه اي از رنگ ها به طوري كه هر دو رأس مجاور در گراف داراي رنگ هاي متفاوت باشند . اگر |c|=k باشد، مي گوييم كه گراف G، k رنگ پذير است. حداقل تعداد رنگ هاي ممكن به طوري كه يك رنگ آميزي مناسب از گراف G حاصل شود را عدد كروماتيك گراف G گويند .
به هر حال واضح است در دنياي الگوريتمهاي كامپيوتري با محدودتهاي زيادي مواجه هستيم كه اين گونه مسائل را ميتوان ايجاد كرد. رنگ آميزي راسي : تخصيص رنگ 1 و 2 و… و به رئوس را رنگ ـ آميزي راسي ناميم.
رنگ آميزي سره :رنگ آميزي سره است كه هيچ دو راس مجاور متمايزي داراي يك رنگ نباشد ..رنگ آميزي راسي سره را به اختصار رنگ ناميم.به طور مشابه، رنگ پذير راسي را به اختصار ، رنگ پذير مي خوانيم.به وضوح گراف، رنگ پذير است اگر و تنها اگر گراف ساده زمينه آن، نگ پذير باشد.
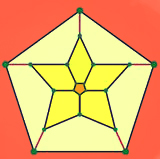
در نظریه گراف، رنگ آمیزی کامل یک نوع از رنگ آمیزی یالها و راسهای گراف می باشد. اگر این نوع از رنگ آمیزی بدون هیچ شرط و قیدی بیان شود معمولاً اینگونه است که هیچ راسی، هیچ یال متلاقی و همچنین هیچ یال و رئوس دو سر آن یک رنگ نباشند. عدد رنگی کامل (χ″(G یک گراف حداقل تعداد رنگهای لازم برای رنگ آمیزی کامل یک گراف G است. گراف کامل( T = T(G گراف G یک گراف است با این شرایط : اولاً اینکه مجموعه ی رئوس T متناظر باشند با رئوس و یالهای G و دوماً اینکه دو راس در T مجاورند اگر و فقط اگر عناصر متناظر آنها در G یا مجاور باشند و یا متلاقی.