زنگتفریح شماره 134
هرچه بیشتر تمرین یا اثبات کنیم، تمرین یا اثبات کردن برایمان سادهتر میشود.
«سیلوستر»

مقدمه
پال اردوش (P. Erdos) و لوئیس موردل (L. G. Mordell) از برجستهترین ریاضیدانان قرن بیستم هستند. هر دوی آنها چه از لحاظ تئوری و چه از لحاظ کاربرد بهویژه حل مسایل، شهرت بسیاری دارند. اگر چه حل مساله از پائینترین اشکال تحقیق در ریاضیات است، اما هیچ راهی بهتر از آن برای ورود به تحقیقات اصیل وجود ندارد. یکی از ارکان اصلی یادگیری، تمرین بسیار است. برای ورود به بحث لازم است ابتدا قضیهی مشهور از اویلر ذکر شود.
قضیه ی اویلر:
اگر r و R را به ترتیب شعاعهای دایرههای محاطی و محیطی یک مثلث فرض کنیم، خواهیم داشت: R≥2r. تساوی تنها وقتی رخ میدهد که مثلث متساویالاضلاع باشد. |
اثبات:
N، M و L را به ترتیب وسط ضلعهای AB، AC و BC از مثلث ABC در نظر میگیریم. دو مثلث LMN و ABC متشابهند و هر ضلع مثلث LMN نصف ضلع متناظر خود در مثلث ABC است. چون شعاع دایرهی محیطی مثلث ABC برابر R است، بنابراین شعاع دایرهی محیطی مثلث LMN برابر R/2 میشود. دایرهی محاطی مثلث ABC، کوچکترین دایرهای است که تنها در یک نقطه با هر ضلع مثلث مشترک است، بنابراین r≤R/2 است. تساوی زمانی که دایرهی محیطی مثلث LMN بر سه ضلع مثلث ABC مماس، یعنی بر دایرهی محاطی این مثلث منطبق باشد و این در حالتی پیش میآید که مثلث ABC متساویالاضلاع باشد.
قضیهی اویلر را میتوان بهسادگی در فضای سه-بعدی تعمیم داد و بین شعاع دو کرهی محاطی و محیطی یک چهار-وجهی، رابطهای بهدست آورد (این کار را انجام دهید). همین قضیه را میتوان با توجه به برابری (1):
CI2 = R(R+2r) (1)
هم اثبات کرد که در آن، CI عبارت است از فاصلهی بین مرکزهای دو دایرهی محیطی و محاطی مثلث.
در حالتی که این دو مرکز برهم منطبق باشند، با مثلث متساوی الاضلاع سروکار داریم. CI2 مقداری نامنفی است، بنابراین R-2r همواره مثبت است به جز در مثلث متساوی الاضلاع که برابر صفر می شود (اثبات برابری (1) آسان است برای پرهیز از طولانی شدن صرف نظر شده است. این کار را به خواننده واگذار مینمائیم).
|
قضیه ی اردوش- موردل:
اگر R2، R1 و R3 را فاصلههای سه راس مثلث از نقطهی مفروض P در داخل مثلث. و r2، r1 و r3 را فاصلههای همین نقطهی P از سه راس مثلث فرض کنیم، خواهیم داشت:
R1+R2+R3 ≥ 2(r1+r2+r3)
تساوی تنها زمانی رخ میدهد که مثلث متساویالاضلاع و نقطهی P منطبق بر مرکز هندسی مثلث باشد.
|
باید توجه کرد که قضیه قبل را نمیتوان حالت خاصی از این قضیه دانست. عمودهای PL و PM و PN را به ترتیب بر ضلعهای BC و AC و AB فرود میآوریم (شکل زیر) بنابراین:
R1 = PA R2 = PB R3 = PC r1 = PL r2 = PM r3 = PN
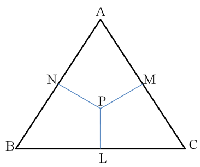
اگر زاویههای راسهای B، A و C را به ترتیب β ،α و γ بنامیم، در مثلث AMN و AMP داریم:
AM. Sinα = NM.Sin(ANM) و R1.Sin(APM)=AM.Sin90° (3)
چون هر یک از زاویههایANP و AMP قائمهاند، بنابراین از چهار نقطهی A، M، P و N میتوان یک دایره گذراند. و در نتیجه، زاویههای ANM و AMP با هم برابر میشوند. با توجه به این نکته، از ضرب دو برابری در (3)، بهدست میآید:
MN = R1.Sinα
زوایای MPN و α مکمل یکدیگرند، بنابراین:
Cos (MPN) = -Cosα
اکنون با توجه به قانون کسینوسها در مثلث PMN داریم:
(MN2=r22+r32+2r2.r3.Cosα (4
و چون α + β = γ = 180° ، بنابراین:
Cosα= -Cos(β+γ) = Sinβ.Sinγ - Cosβ.Cosγ
به این ترتیب برابری (4) بهصورت زیر در میآید:
(MN2=(r2(Sinγ+r3 Sinβ)2 + (r2 Cosγ - r3 Cosβ)2 ≥ (r2 Sinγ + r3 Sinβ)2 (5
اما MN = R1Sinα. بنابراین:
(R1 ≥ r2.(Sinγ/Sinα)2 + r3.(Sinβ/Sinα)2 (6
اگر نابرابری های مشابه (6) را برای R2 و R3 بنویسیم، نسبت به r2 ،r1 و r3 منظم کنیم، نابرابری X+1/X ≥ 2 را، برای هر مقدار متبت X در نظر بگیریم (علامت برابر تنها برای X=1 برقرار است)، به همان نابرابری (2) میرسیم (نابرابری X+1/X ≥ 2 ، به ترتیب برای X=sinγ/sinα,sinα/sinβ,sinβ/sinγ بهدست میآید).
بررسی این که نابرابری 2 در چه حالتی به برابری تبدیل میشود هم آسان است و هم آموزنده. به دانشآموزان واگذار میگردد.
قضیههای این بخش به اویلر، اردوش و موردل تعلق دارند اما این تنها بخش بسیار کوچکی از کارهای گستردهی این ریاضیدانان است. لئونارد اویلر (1783-1707) در تمامی شاخههای ریاضیات سهم عمدهای دارد. بسیاری از نمادها و نشانهگذاریهای امروز را مدیون او هستیم. بهعنوان مثال این بود که برای نخستین بار نماد π (حرف پی در لاتین) را برای نسبت محیط دایره به قطر آن در نظر گرفت و همچنین نماد e را به عنوان ثابت اصلی ریاضیات (که دربارهی آن صحبت شده است) معرفی کرد.
غلامرضا پورقلی
دانشجوی دکتری ریاضی
دانشگاه تهران