یک چندضلعی دل‌خواه روی کاغذ بکشید. این چند ضلعی ممکن است محدب یا مقعر باشد، ولی دقت کنید خودش را قطع نکند، یعنی هیچ دو ضلع نامجاوری با هم اشتراک نداشته باشند. حال تعداد دل‌خواهی نقطه نیز درون چندضلعی قرار دهید.

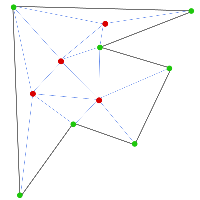
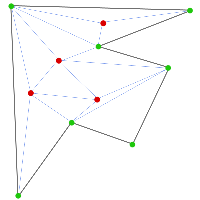
اگر چندضلعی شما n زاویه داشته باشد و تعداد نقطه‌هایی که شما در چندضلعی قرار داده‌اید m باشد، n+m نقطه دارید که می‌توان از به هم وصل کردن آنها چندضلعی را مثلث‌بندی کرد، یعنی چندضلعی به‎طور کامل با مثلث‌ها پوشانده شود جوری که هیچ کدام از نقطه‌ها روی هیچ ضلعی از این مثلث‌ها قرار نگیرد. دقت کنید که این مثلث‌بندی یکتا نیست، یعنی با همین نقطه‎ها می‎توان مثلث‌بندی دیگری برای چندضلعی پیدا کرد.

اما نکته‌ای که در دو مثلث‌بندی زیر می‌توانید ببینید این است که تعداد مثلث‎ها تغییر نکرده است. آیا این موضوع برای همه‌ی مثلث‌بندی‎ها برقرار است؟ اگر جوابتان مثبت است آن را اثبات کنید و تعداد مثلث‌ها را بر حسب m و n بیابید.