پازل جایگشتی یک بازی فکری است که در آن باید با انجام یک سری تغییرات در اجزای بازی، نظمی خاص بین این اجزا برقرار شود. در نگاه اول این بازیها بسیار ساده به نظر میآیند، ولی اکثر آنها از پیچیدگیهای خاصی برخوردارند. یکی از دلایلی که این بازیها را جایگشتی میگویند آن است که شکل تغییرات مکانی یا جابهجاییها بین اجزای بازی بوسیله گروه جایگشتها که مفهمومی جبری و هندسی است، انجام میشود. فرض کنید یک مجموعه با n عضو و دقیقا n جای خالی دارید که میتوانید عناصر مجموعه را در آنها قرار دهید. توجه کنید که این جاهای خالی مرتباند و یا به عبارتی شمارهدار هستند. مثلا فرض کنید {M={a,b,c,d,e مجموعه مورد نظر و جاهای خالی به شکل زیر باشند.
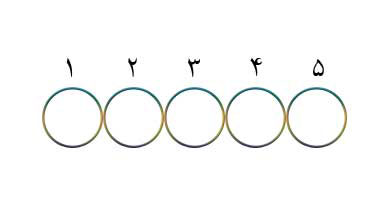
محاسبه تعداد حالتهایی که میتوانیم اعضای مجموعه M را در این جاها قرار دهیم کار آسانی است. برای مکان اول ۵ انتخاب وجود دارد. چون یکی از عناصر M را در جای اول قرار دادیم پس برای جای دوم ۴ انتخاب باقی میماند و به همین ترتیب برای جاهای سوم و چهارم و پنجم به ترتیب ۳ و ۲ و ۱ انتخاب باقی میماند. در نتیجه تعداد حالاتی که بتوانیم عناصر M را در این جاها قرار دهیم برابر است با !۵=۲۴۰=۱×۲×۳×۴×۵. در ریاضی هر کدام از این ۲۴۰ حالت را یک جایگشت از گروه ۵ عضوی M گویند. به همین روش تعداد جایگشتهای یک مجموعه n عضوی برابر است با !n.
 |
مکعب روبیک در سال ۱۹۷۴ توسط ارنو روبیک (Ernő Rubik) مجسمهساز و استاد معماری مجارستانی اختراع شد. این پازل یکی از بازیهای جایگشتی بسیار جالب است که پس از گذشت بیش از ۴۰ سال از اختراع آن همچنان پرطرفدار است. این پازل در ظاهر بسیار ساده است ولی در واقع حل کردن آن بسیار پیچیده است. تعداد بسیار کمی از مردم تا کنون این پازل را حل کردهاند و تعداد بسیار کمتری بدون استفاده از راهنمایی کتاب یا سایتهای اینترنتی خاص به حل آن پرداخته اند. ارنو روبیک چندین هفته وقت صرف کرد تا بالاخره موفق شد این مکعب را منظم کند.
هدف ما از این مقاله آموزش حل کردن معمای روبیک نیست. بلکه میخواهیم نشان دهیم این بازی ظاهرا ساده چقدر گسترده و پیچیده است. پس از گذشت چند دهه از اختراع مکعب روبیک دانشمندان هنوز به دنبال مسائل جدید در مورد آن هستند. مثلا دو ریاضیدان به نامهای داویدسون و روکیکی در سال ۲۰۱۰ با استفاده از محاسبات ابررایانهها نشان دادند که عدد خدا برای مکعب روبیک ۲۰ است. یعنی یک مکعب روبیک با نامنظمترین شکل ممکن را با ۲۰ حرکت میتوان منظم کرد.
 |
تعداد حالتهایی که میتوان یک مکعب روبیک را به هم ریخت، برابر است با عدد باورنکردنی ۴۳ میلیارد میلیارد (مطمئن باشید این عدد اشتباه تایپی نیست) که میتوان آن را به سادگی ۱۰۱۹×۴.۳ نوشت. این عدد واقعا بزرگ است ولی به هرحال متناهی است. بنابراین باید حالت یا حالتهایی وجود داشته باشند که نسبت به همه حالتهای دیگر نامنظمتر و پیچیدهترند. چندین سال است دانشمندان اعتقاد دارند که فقط تعداد محدودی از حالتهای مکعب روبیک وجود دارد که برای حل آنها به ۲۰ حرکت نیاز داریم و بقیه حالات با کمتر از ۲۰ حرکت حل میشوند. تنها مثال موجود از مکعبی که به هر ۲۰ حرکت نیاز دارد Superflip نامیده میشود که به شکل زیر است.

در سالهای اخیر برنامههای کامپیوتری بسیاری نوشته شدهاند که میتوانند هر مکعب روبیک را با حداقل تعداد حرکت و در کمترین زمان (شاید کمتر از یک ثانیه) حل کنند. حتی شما هم میتوانید روی رایانه شخصی خود این برنامهها را اجرا کنید. ممکن است فکر کنید این برنامهها میتوانند مساله پیچیدهترین مکعب روبیک را حل کنند؛ به این صورت که با استفاده از این برنامهها همه مکعبهای روبیک را حل کنیم و آن مکعبهایی را که به بیشترین تعداد حرکت نیاز دارند را به عنوان پیچیدهترین مکعب انتخاب کنیم. مشکل اینجاست که تعداد حالات متمایز مکعب روبیک ۴۳ میلیارد میلیارد است و حتی اگر برنامهای بتواند در هر ثانیه ۱ میلیون حالت را حل کند، باز هم حدود ۱ میلیون سال طول میکشد تا همه حالات حل شوند.
داویدسون و روکیکی (Davidson and Rokicki) توانستند با اقدامی بسیار هوشمندانه برای یافتن کمترین تعداد حرکت برای پیچیدهترین حالتهای مکعب، از بین ۴۳ میلیارد میلیارد حالت ممکن فقط چند میلیارد حالت را مشخص کنند که از همه پیچیدهترند و با استفاده از امکانات مرکز ابررایانه اهایو در عرض چند روز محاسبه این حالات به پایان رسید.
پازلهای جایگشتی قبل از مکعب روبیک نیز وجود داشتهاند. برای مثال پازل ۱۵ که یک بازی بسیار ساده است حدود صد سال قبل از مکعب روبیک در سال ۱۸۸۰ در ایالات متحده اختراع شد. این پازل شامل ۱۵ قطعه مربعی در یک شبکه ۱۶ خانهای است که مربعها از ۱ تا ۱۵ شمارهگذاری شده اند.
سام لوید (Sam Loyd) که به او لقب حل کننده پازل نابغه داده بودند، برای کسی که بتواند در پازل ۱۵ با انجام یک سری حرکت جای اعداد ۱۵ و ۱۴ را با هم عوض کند و بقیه اعداد سر جای اول خود قرار گیرند یک جایزه ۱۰۰۰ دلاری در نظر گرفته بود. البته احتمالا او بسیار به خودش افتخار میکرده ولی قبل از اختراع پازل ۱۵ در سال ۱۸۷۹ دو ریاضیدان به نامهای جانسون و استوری (Johnson and Story) نشان داده بودند که انجام این کار غیرممکن است.
احتمالا قدیمیترین پازلی که به جایگشت قطعات هندسی بستگی دارد، استاماچیون (Ostomachion) است. این پازل از بریدن یک مربع به ۱۴ قسمت که هرکدام از این قسمتها محدّب هستند به وجود میآید. اگر این قطعات را از هم جدا کنید و بخواهید با آنها دوباره مربع بسازید واقعا به دردسر خواهید افتاد.
ریاضیدان دوره باستان، ارشمیدس، رسالهای در مورد استاماچیون نوشته بود. این رساله تا چند سال پیش مفقود بود ولی باستانشناسان اخیرا موفق به بازیابی قسمتهایی از این رساله شدند. ارشمیدس در کتاب خود در مورد تعداد حالتهای متمایزی که میتوان این ۱۴ قطعه را کنار هم قرار داد تا یک مربع به دست آید سوال میکند. شاید ارشمیدس به این سوال جواب داده باشد ولی در اسناد بازیابی شده از او جواب این سوال پیدا نشد. در هر صورت یک ریاضیدان به نام بیل کاتلر (Bill Cutler) با استفاده از کامپیوتر این مساله را حل کرد. تعداد ۱۷۱۵۲ جایگشت متفاوت از این قطعات وجود دارد که میتوان با آن یک مربع ساخت.
منابع: