«اعداد» را ميتوان به دستههاي مختلفي نظير ذيل تقسيم كرد:
| - اعداد «گنگ» (Irrational) و «گويا» (Rational) | | - اعداد «حقيقي» (Real) و «مختلط» (Complex) | | - اعداد «موهومي» (Imaginary) | | - اعداد «جبري» (Algebraic) و «غيرجبري» (Transcendental) | | - اعداد «كامل» (Perfect) | | - اعداد «سورئال» (Surreal) | | - اعداد «مثلثي» (Triangle) و «مربعي» (Square) | | - و ... |
| اعداد «گنگ» (Irrational) و «گويا» (Rational) |
عدد «گويا» (Rational) عددي حقيقي است كه بتوان آن را بهصورت كسري از دو عدد صحيح (نظير: 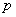 و و .png) ) نوشت بهعبارت ديگر داشته باشيم: ) نوشت بهعبارت ديگر داشته باشيم:
(رابطهي 1)
در رياضيات اين گزاره صحيح نيست كه: «هر عددي «گويا» نباشد «گنگ» است». اعدادي نيز وجود دارند كه نه «گويا» هستند و نه «گنگ» نظير: اعداد بينهايت كوچك. اگر بخواهيم از اعداد «گنگ» مثال بزنيم ميتوانيم به مواردي نظير ذيل اشاره كنيم:
| - .png) ، ، .png) و ... و ... | | - عدد .png) | | - عدد «طلايي» (Golden Mean) .png) . . | | - عدد e. |
بسط دهدهي يك عدد «گنگ» نشان ميدهد كه داراي ويژگيهايي نظير ذيل هستند:
| - بيپايان هستند. | | - تكرارناپذير هستند يعني رقمهاياشان الگويي غيرتكراري را نشان ميدهد. |
ميتوان اصلهايي نظير ذيل را دربارهي اعداد «گنگ» (Irrational) و «گويا» (Rational) اثبات كرد:
.gif)
| «ژرژ كانتور»
(George Cantor) |
اجتماع اعداد «گويا» و «گنگ»، اعداد «حقيقي» است. بهعبارت ديگر اعداد «حقيقي» ممكن است «گويا» يا «گنگ» باشند. «ژرژ كانتور» (George Cantor) رياضيدان آلماني نشان داده است در حالي كه بينهايت عدد «گويا» و «گنگ» وجود دارد تعداد اعداد «گنگ» از اعداد «گويا» بيشتر است.
| اعداد «حقيقي» (Real) و «مختلط» (Complex) |
اعداد «مختلط» زوجهاي .png) از دو عدد حقيقي هستند. توسعهي نظريهي اعداد «مختلط» از آنجا ناشي شد كه رابطهي سادهي ذيل در مجموعهي اعداد حقيقي حلنشدني بهنظر ميآمد: از دو عدد حقيقي هستند. توسعهي نظريهي اعداد «مختلط» از آنجا ناشي شد كه رابطهي سادهي ذيل در مجموعهي اعداد حقيقي حلنشدني بهنظر ميآمد:
(رابطهي 2) در مجموعهي اعداد «مختلط» رابطهي 2 داراي دو جواب است:
(رابطهي 3)
بقيهي اعداد «مختلط» از جمع اين عدد جديد .png) با مجموعهي اعداد صحيح بهدست ميآيد. همچنين لازم است بهكار بردن عمليات حسابي معمول (جمع، تفريق و ضرب) و همهي قوانين شناخته شده براي آن، جهت توسعهي مجموعهي اعداد «مختلط» بديهي فرض شود. بدينترتيب اصطلاحاً گفته ميشود مجموعهي اعداد «مختلط» نسبت به عمليات حسابي معمول، «بسته» است. با مجموعهي اعداد صحيح بهدست ميآيد. همچنين لازم است بهكار بردن عمليات حسابي معمول (جمع، تفريق و ضرب) و همهي قوانين شناخته شده براي آن، جهت توسعهي مجموعهي اعداد «مختلط» بديهي فرض شود. بدينترتيب اصطلاحاً گفته ميشود مجموعهي اعداد «مختلط» نسبت به عمليات حسابي معمول، «بسته» است. اعداد «مختلط» ويژگيهاي غيرمعمولي را بهخصوص هنگام مشتقگيري از خود نشان ميدهند:
| - مشتقگيري از اعداد «حقيقي» نقطهي آغاز «آناليز حقيقي» (Real Analysis) و «حساب ديفرانسيل و انتگرال» (Calculus) است. | | - مشتقگيري از اعداد «مختلط» ما را به «نظريهي توابع تحليلي» (Analytic Function Theory) رهنمون ميكند. |
| اعداد «موهومي» (Imaginary) |
هر عدد «مختلط» از يك زوج عدد حقيقي نظير: .png) تشكيل شده است. تشكيل شده است. .png) در اين زوج، «قسمت حقيقي» و در اين زوج، «قسمت حقيقي» و .png) «قسمت موهومي» ناميده ميشود. «قسمت موهومي» ناميده ميشود.
عدد «مختلط» .png) با نقطهي با نقطهي .png) در سيستم مختصات استاندارد در صفحه مشخص ميشود. نقاط در سيستم مختصات استاندارد در صفحه مشخص ميشود. نقاط .png) بر روي محور بر روي محور .png) و نقاط و نقاط .png) بر روي محور بر روي محور .png) قرار دارند. زماني كه از لحاظ جبري بر ماهيت اعداد «مختلط» تأكيد ميشود مرسوم است بهشكل ذيل نوشته شود: قرار دارند. زماني كه از لحاظ جبري بر ماهيت اعداد «مختلط» تأكيد ميشود مرسوم است بهشكل ذيل نوشته شود:
(رابطهي 4)
بدينترتيب بين «قسمت حقيقي» .png) و «قسمت موهومي» و «قسمت موهومي» .png) تفاوت محسوسي قايل ميشوند. اما به هر حال موقعيتهايي وجود دارد كه كلمهي «موهومي» توصيفهاي مناسبي از آن موقعيتها را فراهم ميكند. تفاوت محسوسي قايل ميشوند. اما به هر حال موقعيتهايي وجود دارد كه كلمهي «موهومي» توصيفهاي مناسبي از آن موقعيتها را فراهم ميكند. در صفحه، مجذور فاصلهي بين دو نقطهي .png) و و .png) بهصورت ذيل بيان ميشود: بهصورت ذيل بيان ميشود:
(رابطهي 5)
اين عدد .png) طبق «قضيهي فيثاغورث» عددي كاملاً «طبيعي» است. پس دايرهاي با شعاع طبق «قضيهي فيثاغورث» عددي كاملاً «طبيعي» است. پس دايرهاي با شعاع .png) بهمركز بهمركز .png) از نقطهي از نقطهي .png) ميگذرد بهگونهاي كه داشته باشيم: ميگذرد بهگونهاي كه داشته باشيم:
(رابطهي 6)
بهعبارت ديگر داريم:
(رابطهي 7)
اين معادلهاي از يك دايرهي حقيقي در صفحهاي حقيقي (شامل: اعداد «مختلط») است بهعنوان مثال: شكلي است كه توسط يك پرگار كشيده ميشود. بنابراين رياضيدانان در رابطهي .png) متوقف نشدهاند بلكه مسألهي مهم در اين رابطه، علامت عدد 1 در اين رابطه است. متوقف نشدهاند بلكه مسألهي مهم در اين رابطه، علامت عدد 1 در اين رابطه است. رابطهي جديد .png) مبدأي براي كشفهايي در 250 سال اخير شده است. در ادامهي حالتهاي غيرمعمول، رياضيدانان تنها بر تغيير علامتهاي رابطهي 7 متوقف نشدند. از آنجايي كه داريم: مبدأي براي كشفهايي در 250 سال اخير شده است. در ادامهي حالتهاي غيرمعمول، رياضيدانان تنها بر تغيير علامتهاي رابطهي 7 متوقف نشدند. از آنجايي كه داريم:
(رابطهي 8)
آنها رابطهي ذيل را نتيجه گرفتند:
(رابطهي 9)
اين رابطه واقعاً مربوط به يك دايرهي تصوري است كه داراي يك مركز واقعي .png) با شعاع با شعاع .png) است. است. علاوه بر اين، ممكن است گفته شود معادلهي 9 شامل چندجملهاي داراي جوابهاي واقعي .png) يا جوابهاي «مختلط» نيست. اما به هر حال براي سادگي دايرهاي به مركز مبدأ مختصات درنظر ميگيريم لذا داريم: يا جوابهاي «مختلط» نيست. اما به هر حال براي سادگي دايرهاي به مركز مبدأ مختصات درنظر ميگيريم لذا داريم:
(رابطهي 10)
واضح است كه رابطههاي 9 و 10 داراي جوابهايي است. بهعنوان مثال، زوج .png) در رابطهي 10 صدق كرده شايد واقعاً يك عدد «موهومي» ناميده شود. در رابطهي 10 صدق كرده شايد واقعاً يك عدد «موهومي» ناميده شود.
هر عددي نظير: .png) حداقل بر 1 و حداقل بر 1 و .png) بخشپذير است. جمع همهي مقسومعليههاي عدد بخشپذير است. جمع همهي مقسومعليههاي عدد .png) با نماد با نماد .png) نشان داده ميشود. نشان داده ميشود. اگر رابطهي ذيل را داشته باشيم:
(رابطهي 11)
كه در آن .png) همگي «عدد اول» باشند، عدد همگي «عدد اول» باشند، عدد.png) «كامل» (Perfect) است اگر برابر جمع مقسومعليههاي عدد شامل 1 (بهاستثناي «كامل» (Perfect) است اگر برابر جمع مقسومعليههاي عدد شامل 1 (بهاستثناي .png) ) باشد. بهعبارت ديگر عددي «كامل» (Perfect) است اگر داشته باشيم: ) باشد. بهعبارت ديگر عددي «كامل» (Perfect) است اگر داشته باشيم:
(رابطهي 12) بهعكس اگر عددي «كامل» نباشد دو حالت ممكن است وجود داشته باشد:
|  .png) (اعداد «ناكامل») (Deficient) (اعداد «ناكامل») (Deficient) | |  .png) (اعداد «وافر») (Abundant). (اعداد «وافر») (Abundant). |
 اعداد «ناكامل» (Deficient) اعداد «ناكامل» (Deficient)
اعدادي كه دربارهي آنها رابطهي ذيل صادق باشد عدد «ناكامل» (Deficient) ناميده ميشوند:
(رابطهي 13)
بهعنوان مثال:
(رابطهي 14)
همچنين داريم:
(رابطهي 15)
بنابراين 8 و 15 اعداد «ناكامل» هستند.
 اعداد «وافر» (Abundant) اعداد «وافر» (Abundant)
اعدادي كه دربارهي آنها رابطهي ذيل صادق باشد اعداد «وافر» (Abundant) ناميده ميشود:
(رابطهي 16)
بهعنوان مثال: 12 عددي «وافر» است زيرا داريم:
«اقليدس» در جلد نهم كتابش با عنوان: «عناصر» .png) ثابت كرده است اگر براي عدد اولي نظير: ثابت كرده است اگر براي عدد اولي نظير: .png) رابطهي ذيل صادق باشد عدد رابطهي ذيل صادق باشد عدد .png) عددي «كامل» است: عددي «كامل» است:
(رابطهي 17)
«لئونارد اويلر» (Leonard Euler) در مقالهاي كه پس از مرگش منتشر شد نشان داد كه هر عدد «كامل» زوج داراي شكل اقليدسي است. اين در حالي است كه وي در 18 سال آخر زندگياش رنج نابينايي را متحمل ميشد. بنابراين محتملاً اين نتيجه مربوط به زمان قبل از نابينايياش بوده است. بنابراين اولين عدد «كامل» 6 و عدد بعد از آن 28 است زيرا داريم:
(رابطهي 18)
بعد از آن ميتوان از اعداد 496، 8128 و ... نام برد. پنجمين عدد «كامل» 33550336 است كه توسط محققي بهنام «هودالريكس رجيوس» (Hudalrichus Regius) حدود 500 سال قبل بهعنوان عدد «كامل» معرفي شد.
اعداد «سورئال» (Surreal) توسط محققي بهنام «جان كانوي» (John Conway) همراه با چيزهاي ديگر در حين طراحي «بازي زندگي» (Game of Life) كشف شد. محققي بهنام «دونالد كنوث» (Donald Knuth) در بروشوري با عنوان: «اعداد سورئال» (Sureal Numbers) طي مقدمهاي اعداد مذكور را چنين توصيف كرده است:
يك «عدد سورئال» زوجي از مجموعههاي .png) است كه در آن انديسهاي است كه در آن انديسهاي .png) بيانگر محل نسبي (راست و چپ) مجموعهها در زوج مذكور است. اولين عدد «سورئالي» كه بايد ايجاد شود «صفر» بيانگر محل نسبي (راست و چپ) مجموعهها در زوج مذكور است. اولين عدد «سورئالي» كه بايد ايجاد شود «صفر» .png) است كه مجموعههاي «راست» و «چپ» هر دو «تهي» هستند. بقيهي اعداد «سورئال» از «صفر» آغاز و تنها دو قانون ساده در مورد آنان بهكار ميرود. واقعاً بايد گفت: «از هيچ، چنين خلقتي انجام شده است!». است كه مجموعههاي «راست» و «چپ» هر دو «تهي» هستند. بقيهي اعداد «سورئال» از «صفر» آغاز و تنها دو قانون ساده در مورد آنان بهكار ميرود. واقعاً بايد گفت: «از هيچ، چنين خلقتي انجام شده است!».
«مارتين گاردنر» (Martin Gardner) كاربرد اعداد «سورئال» را در «نظريهي بازيها» توضيح داد و «جان كانوي» (John Conway) آن را بسط داده است.
| اعداد «مثلثي» (Triangle) و «مربعي» (Square) |
 اعداد «مربعي» (Square) اعداد «مربعي» (Square)
هركسي ميداند چگونه «مربع يك عدد» را محاسبه كند بهخصوص وقتي عدد مذكور خيلي بزرگ نباشد. بهعنوان مثال: .png) و ... و ... اما راستي چرا عمليات «ضرب يك عدد در خودش»، «مربع» آن عدد ناميده ميشود؟ علت آن را ميتوان از شكل 1 دريافت. .gif)
| شكل 1 – شكلي از
اعداد «مربعي» (Square). |
يك مربع با ضلع .png) ميتواند شبكهاي شامل تعداد ميتواند شبكهاي شامل تعداد .png) از مربعهايي متصور شود كه هر مربع داراي اندازهاي معادل از مربعهايي متصور شود كه هر مربع داراي اندازهاي معادل .png) باشد. باشد.
 اعداد «مثلثي» (Triangle) اعداد «مثلثي» (Triangle) وجه تسميهي اعداد «مثلثي» بهعلت شباهت ساختار آنها به «مثلث» است. اعداد «مثلثي» شامل اعدادي نظير ذيل هستند: 1، 3، 6، 10، 15 و ... فرمول عمومي براي هر عدد «مثلثي» .png) عبارت است از: عبارت است از:
(رابطهي 19)
عدد .png) «مثلثي» است و تعداد نقطههايي را نشان ميدهد كه در شكلي مثلثي با «مثلثي» است و تعداد نقطههايي را نشان ميدهد كه در شكلي مثلثي با .png) ضربدر نظير شكل 2 قرار گرفتهاند. ضربدر نظير شكل 2 قرار گرفتهاند. .gif)
|
شكل 2 – شكلي از
اعداد «مثلثي» (Triangular).
|
البته لازم است ثابت شود تعداد كل ضربدرها كه در شكل 2 نشان داده شده از رابطهي 19 محاسبه ميشود. اما به هر حال مشاهده ميكنيم كه تعداد ضربدرها در هر مثلث از جمع اعداد طبيعي بهدست ميآيد:
(رابطهي 20)
براي اثبات اين رابطه از شكل 3 استفاده ميكنيم: .gif)
|
شكل 3 – اثبات
رابطهي مربوط به
اعداد «مثلثي»
.png) . . |
بهعلاوه دو مثلث با .png) ضربدر در هر ضلع، «مستطيلي» با ضربدر در هر ضلع، «مستطيلي» با .png) ضربدر تشكيل خواهند داد. ممكن است سؤال شود مگر با نقطهگذاري در شكل ميتوان چيزي را ثابت كرد. البته جواب منفي است بلكه شكل در درك و تشخيص اثبات كمك ميكند. بهعلاوه بهطرق ديگري نيز براي اثبات اين مطلب وجود دارد. ضربدر تشكيل خواهند داد. ممكن است سؤال شود مگر با نقطهگذاري در شكل ميتوان چيزي را ثابت كرد. البته جواب منفي است بلكه شكل در درك و تشخيص اثبات كمك ميكند. بهعلاوه بهطرق ديگري نيز براي اثبات اين مطلب وجود دارد. اين جمع بيانگر تعداد ضربدرها در يك «مثلث» است. دو مثلثي كه با زاويهي 180 درجه دوران كرده مجموعاً تشكيل يك مستطيل ميدهند. در هر رديف بهتعداد مساوي ضربدر وجود دارد. در اولين رديف اگر .png) ضربدر وجود داشته باشد در رديف دوم ضربدر وجود داشته باشد در رديف دوم .png) ضربدر و در رديف ...، ... ضربدر و ... وجود خواهد داشت. بدينترتيب در رديفها بهصورت كاهشي تعداد ضربدر و در رديف ...، ... ضربدر و ... وجود خواهد داشت. بدينترتيب در رديفها بهصورت كاهشي تعداد .png) ضربدر خواهيم داشت. ضربدر خواهيم داشت. براي اثبات از طريق جبري، دو جمع را به صورت ذيل در نظر ميگيريم:
| - يكي افزايشي | | - ديگري كاهشي. |
(رابطهي 21)
اكنون در رابطهي 21 جملهها را با تركيب جملههاي اول، دوم و ... مجدداً طبقهبندي ميكنيم؛ در اين صورت خواهيم داشت:
(رابطهي 22)
بدينترتيب رابطهي 19 بهدست ميآيد.
| قضيهي هورويتز (Hurwitz' Theorem) |
بسط دهدهي يك عدد «گنگ»، دنبالهاي آشنا از تقريبهاي گوياي آن است. بهعنوان مثال: عدد «پي» .png) - كه عددي «گنگ» است - را ميتوان بهصورت ذيل نوشت: - كه عددي «گنگ» است - را ميتوان بهصورت ذيل نوشت:
(رابطهي 23)
ميتوانيم دنبالهاي با تقريب هرچه بيشتر از عدد .png) را معرفي كنيم. ميتوانيم «كيفيت» دنبالهي مذكور را با ياداوري رابطهي ذيل اندازه بگيريم: را معرفي كنيم. ميتوانيم «كيفيت» دنبالهي مذكور را با ياداوري رابطهي ذيل اندازه بگيريم:
(رابطهي 24)
بدينترتيب خطاي محاسبه در مقسومعليه كسر كمتر از «يك» خواهد بود. بهطور مشابه عدد گنگي نظير: .png) را بهطور تقريبي - با همان دقتي كه در محاسبهي عدد را بهطور تقريبي - با همان دقتي كه در محاسبهي عدد .png) وجود دارد - با دنبالهاي از اعداد نظير ذيل ميتوان بيان كرد: وجود دارد - با دنبالهاي از اعداد نظير ذيل ميتوان بيان كرد:
(رابطهي 25)
مشاهدهي روابطي نظير: 23 و 25 رياضيدانان را به طبقهبندي اعداد «گنگ» واداشته است؛ بهعبارت ديگر، اعداد «گنگ» را با توجه به چگونگي سختي محاسبهاشان از طريق «تقريب» با اعداد «گويا» طبقهبندي كردهاند. بهعبارت ديگر يك عدد «گنگ» از عدد «گنگ» ديگر گنگتر است! براي بهدست آوردن «ملاك تقريب» از حقيقت ذيل استفاده ميكنيم: «هر عددي داراي تقريبهاي «گوياي» بينهايتي بهشكل .png) است كه در آن، تقريب است كه در آن، تقريب .png) داراي خطايي كمتر از داراي خطايي كمتر از .png) است». است». گزارهي بالا «قضيهي هورويتز» (Hurwitz' Theorem) ناميده ميشود. بنابراين «ملاك تقريب» برحسب اينكه چقدر از .png) كمتر است بهدست ميآيد. در مقام مقايسه، عدد كمتر است بهدست ميآيد. در مقام مقايسه، عدد .png) داراي «تقريب» بهتري نسبت به عدد داراي «تقريب» بهتري نسبت به عدد .png) است. بنابراين است. بنابراين .png) «گنگتر» از «گنگتر» از .png) عدد است (جدول 1). عدد است (جدول 1).
جدول 1 – مقادير .png) ، «خطا» ، «ملاك تقريب» ، «خطا» ، «ملاك تقريب» .png)
و نسبت براي مقايسهي اعداد «گنگ» .png) و و .png) . . | .png)
| .png)
| .png)
| .png)
| .png)
| | 7/22 | 00126/0 | 0091/0 | 13/0 | | 113/355 | 000000266/0 | 0000350/0 | 007/0 | .png)
| .png)
| .png)
| .png)
| .png)
| | 5/7 | 0142/0 | 0179/0 | 79/0 | | 169/239 | 0000124/0 | 0000156/0 | 79/0 |
گنگترين عدد «گنگ» عددي است كه قبلاً در هندسه شناخته شده است. اين عدد عبارت است از:
(رابطهي 26)
عدد «گنگ» .png) عبارت است از: «قطر يك پنجضلعي با اضلاع برابر 1». اين عدد - كه به «عدد طلايي» (Golden Mean) شهرت يافته است - نقش مهمي در مبحث «زيباشناسي رياضي» (Mathematical Aesthetics) دارد. گنگي بسيار بالاي اين عدد، باعث كاربردش در كاربردهاي هنري است كه هنوز علت آن مشخص نشده است. عبارت است از: «قطر يك پنجضلعي با اضلاع برابر 1». اين عدد - كه به «عدد طلايي» (Golden Mean) شهرت يافته است - نقش مهمي در مبحث «زيباشناسي رياضي» (Mathematical Aesthetics) دارد. گنگي بسيار بالاي اين عدد، باعث كاربردش در كاربردهاي هنري است كه هنوز علت آن مشخص نشده است. عدد «طلايي» (Golden Mean) جواب معادلهي ذيل است:
(رابطهي 27)
اين عدد را ميتوان با بسط سادهي نامتناهي ذيل نشان داد:
(رابطهي 28)
تقريبهاي عدد «طلايي» (Golden Mean) عبارتاند از:
(رابطهي 29)
كه همان نسبتهاي توالياي از اعداد «فيبوناچي» (Fibonacci) محسوب ميشوند. سؤالي كه مطرح ميشود آن است كه تقريبهاي عدد «طلايي» (Golden Mean) چگونه است؟ براي پاسخ به اين سؤال، چند عدد مربوط به نسبت .png) در جدول 2 بيان شده است. در جدول 2 بيان شده است. جدول 2 – چند مقدار از تقريبهاي عدد «طلايي» (Golden Mean) و نسبت .png) . . | تقريب .png) | .png)
| .png)
| .png)
| .png)
| .png)
| .png)
| .png)
| .png)
| .png)
| .png)
| .png)
| .png)
| .png)
| .png)
| .png)
| .png)
| .png)
|
«قضيهي هورويتز» (Hurwitz' Theorem) وجود نامحدود تقريبهاي .png) را تضمين ميكند. در اين حالت همانطور كه در جدول 2 مشاهده ميشود، تقريبهاي «فرد» را بايد رها كرد و تقريبهاي «زوج» نيز بد و بدتر ميشوند. در واقع جدول 2 شاهدي است بر اين مدعا كه را تضمين ميكند. در اين حالت همانطور كه در جدول 2 مشاهده ميشود، تقريبهاي «فرد» را بايد رها كرد و تقريبهاي «زوج» نيز بد و بدتر ميشوند. در واقع جدول 2 شاهدي است بر اين مدعا كه .png) در «قضيهي هورويتز» (Hurwitz' Theorem) نميتواند اصلاح شود!! در «قضيهي هورويتز» (Hurwitz' Theorem) نميتواند اصلاح شود!! بنابراين عدد «طلايي» (Golden Mean) نميتواند داراي تقريب نسبي بهتر از 7/22 براي عدد .png) و حتي بهتر از 5/7 براي عدد و حتي بهتر از 5/7 براي عدد .png) باشد. باشد.
.gif)
| شكل 4 – تصويري از
شاخكهاي ميوهي كاج. |
رديابي رشد شاخكهاي ميوهي كاج نشان ميدهد آنها يكييكي از قسمت پاييني اضافه ميشوند. زاويهي بين يك شاخك با ديگري هميشه يكسان است! اين فرض معقول است كه معمولاً مؤثرترين فشردگي زماني اتفاق بيافتد كه اين زاويه تا آنجا كه ممكن است عددي «گنگ» باشد؛ بههمين خاطر است كه در طبيعت، زاويههاي «گنگ» فراوان ديده ميشود. شكل سادهاي از اين حقيقت در فشردگي مثلثها حول يك استوانه مشاهده ميشود (شكل 5). در شكل 5 استوانههاي مورد نظر، برش خورده و گسترده شدهاند. آنها بهگونهاي درنظر گرفته شدهاند كه محيطشان برابر عدد 1 باشد. مختصات افقي (محور .png) ) هر مثلث جديد بهگونهاي در نظر گرفته شده كه در فواصل مساوي در سمت راست ديگري قرار گرفته باشد. همچنين مثلثهاي جديد بهگونهاي قرار گرفتهاند كه هميشه زوايا بهپيمانهي 1 كاهش مييابد. ) هر مثلث جديد بهگونهاي در نظر گرفته شده كه در فواصل مساوي در سمت راست ديگري قرار گرفته باشد. همچنين مثلثهاي جديد بهگونهاي قرار گرفتهاند كه هميشه زوايا بهپيمانهي 1 كاهش مييابد.
.gif)
| شكل 6 – نموداري براي تعريف عدد «گنگ» e. |
تعريف عدد گنگ e كار سادهاي نيست. ميتوان تعاريفي نظير ذيل را براي آن بيان كرد: |  e عددي حقيقي و منحصر بهفردي است بهگونهاي كه سطح زير نمودار هذلولي e عددي حقيقي و منحصر بهفردي است بهگونهاي كه سطح زير نمودار هذلولي .png) و محور و محور .png) ها كه بين دو خط ها كه بين دو خط .png) و و .png) محدود است برابر يك باشد (شكل 6). بهعبارت ديگر داريم: محدود است برابر يك باشد (شكل 6). بهعبارت ديگر داريم:
(رابطهي 30)
| |  e عددي است كه مشتق (شيب خط مماس) تابع ذيل در نقطهي e عددي است كه مشتق (شيب خط مماس) تابع ذيل در نقطهي .png) دقيقاً برابر عدد 1 باشد: دقيقاً برابر عدد 1 باشد:
(رابطهي 31)
.gif) |
شكل 7 – نموداري براي تعريف عدد «گنگ» با توجه به رابطهي ذيل:
.png) . .
|
| |  عدد «گنگ» e از رابطهي ذيل بهدست ميآيد: عدد «گنگ» e از رابطهي ذيل بهدست ميآيد:
(رابطهي 32)
| |  حد غيرعادي ذيل براي تعريف عدد «گنگ» e توسط دو رياضيدان بهنامهاي «ناكس» (Knox) و «وارن هيل برادرز» (Warren Hill Brothers) در سال 1377 (1998 ميلادي) معرفي شد: حد غيرعادي ذيل براي تعريف عدد «گنگ» e توسط دو رياضيدان بهنامهاي «ناكس» (Knox) و «وارن هيل برادرز» (Warren Hill Brothers) در سال 1377 (1998 ميلادي) معرفي شد:
(رابطهي 33)
| | | |  سري نامحدود ذيل را ميتوان براي عدد «گنگ» e نوشت: سري نامحدود ذيل را ميتوان براي عدد «گنگ» e نوشت:
(رابطهي 34)
اين سري توسط «سر آيزاك نيوتن» (Sir Isaac Newton) در سال 1048 (1669 ميلادي) تعريف شد.
| |  عدد «گنگ» e توسط «كسر مسلسل» (Continued Fraction) «غيرساده» و زيباي ذيل تعريف ميشود: عدد «گنگ» e توسط «كسر مسلسل» (Continued Fraction) «غيرساده» و زيباي ذيل تعريف ميشود:
(رابطهي 35)
| |  «سريهاي تودرتوي» ذيل را ميتوان براي بيان عدد «گنگ» e نوشت: «سريهاي تودرتوي» ذيل را ميتوان براي بيان عدد «گنگ» e نوشت:
(رابطهي 36)
| |  و ... و ... |
عدد گنگ e بهافتخار رياضيدان سوييسي «لئونارد اويلر» (Leonard Euler) بعضي اوقات عدد «اويلر» (Euler) خوانده ميشود. همچنين بهافتخار رياضيدان اسكاتلندي «جان نپر» (John Napier)، «ثابت نپر» (Napier's Constant) ناميده ميشود.
ياداوري 1 - همانطور كه ميدانيم «جان نپر» (John Napier) رياضيداني بود كه «لگاريتم» را معرفي كرد. ياداوري 2 – عدد گنگ e را نبايد با «عدد ثابت اويلر» (Euler's Constant) .png) - كه بهصورت ذيل تعريف ميشود - اشتباه گرفت: - كه بهصورت ذيل تعريف ميشود - اشتباه گرفت:
(رابطهي 37)
از آنجايي كه e عددي «گنگ» است ارقام آن نامحدود بوده و تكرار نيز نميشود. عدد e يكي از مهمترين اعداد در رياضيات است.
| قضايايي دربارهي عدد گنگ e |
«اويلر» (Euler) ثابت كرد e عددي «گنگ» بوده و داراي «كسرهاي مسلسل» نامحدود ساده است:
(رابطهي 38)
ياداوري 3 – بهطور كلي منظور از «كسر مسلسل» .png) رابطهي ذيل است: رابطهي ذيل است:
(رابطهي 39)
«ژوزف ليو ويل» (Joseph Liouville) در سال 1223 (1844 ميلادي) ثابت كرد e هرگز جواب «معادلهي درجهي دوم با ضرايب صحيح» نخواهد بود. پس از آن «چارلز هرميت» (Charles Hermite) در سال 1252 (1873 ميلادي) ثابت كرد عدد «گنگ» e عددي «غيرجبري» (Transcendental) است. اما به هر حال e كوچكترين عدد «غيرجبري» ممكن با «اندازهي ناگويايي» (Irrationality Measure) ذيل است:
(رابطهي 40)
«جاناتان ساندو» (Jonathan Sondow) در سال 1385 (2006 ميلادي) با استفاده از ساختار e بهعنوان فصل مشترك «دنبالهي متوالي» (Nested Sequence) از بازههاي بسته ثابت كرد e عددي «گنگ» است. وي در اين روش همچنين اندازهاي از «ميزان ناگويايي» (Measure of Irrationality) برحسب «تابع اسمارانداچه» (Smarandache Function) فراهم ميآورد.
(رابطهي 40)
(رابطهي 40) (رابطهي 40) «جاناتان ساندو» (Jonathan Sondow) داد اگر 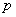 و و .png) هر عدد صحيحي باشند بهگونهاي كه داشته باشيم: هر عدد صحيحي باشند بهگونهاي كه داشته باشيم: .png) آنگاه خواهيم داشت: آنگاه خواهيم داشت:
(رابطهي 41)
ياداوري 4 - «ميزان ناگويايي» (Measure of Irrationality) با .png) نشان داده ميشود تا با «اندازهي ناگويايي» (Irrationality Measure) - كه با نشان داده ميشود تا با «اندازهي ناگويايي» (Irrationality Measure) - كه با .png) نشان داده ميشود - اشتباه نشود. نشان داده ميشود - اشتباه نشود.
«ديويد هـ. بيلي» (David H. Bailey) در سال 1367 (1988 ميلادي) و «پيتر بنيامين بوروين» (Peter Benjamin Borwein) در سال 1368 (1989 ميلادي) ثابت كردند .png) و و .png) جواب معادلههاي چندجملهايها با شرايط ذيل نخواهند بود: جواب معادلههاي چندجملهايها با شرايط ذيل نخواهند بود:
| - از درجهي كمتر از 8 | | - با ضرايب صحيح بهمقدار بهطور متوسط .png) . . |
«وارن هيل برادرز» (Warren Hill Brothers) در سال 1383 (2004 ميلادي) ثابت كرد سري ذيل بيانكنندهي عدد «گنگ» e است:
(رابطهي 42)
حالت خاصي از «فرمول اويلر» (Euler Formula) بهصورت رابطهي ذيل بيان ميشود:
(رابطهي 43)
وقتي .png) باشد رابطهي 43 بهصورت رابطهي زيباي ذيل درميآيد: باشد رابطهي 43 بهصورت رابطهي زيباي ذيل درميآيد:
(رابطهي 44)
«كارل داگلاس الدز» (Carl Douglas Olds) در سال 1342 (1963 ميلادي) رابطههاي ذيل را براي e بيان كرد:
(رابطهي 45)
رياضيداني بهنام «نيل ج. اسلوان» (Neil J. A. Sloane) «كسرهاي مسلسل» متحيركنندهي ذيل را براي توانهاي گوياي عدد e ثابت كرده است:
(رابطهي 46)
|